Материалы для справок
Дискретные распределения.
1 Распределение Бернулли B(p). Случайная величина X имеет распределение Бернулли с параметром p (0<=p<=1) если P(X=1)=p и P(X=0)=1-p. Алгоритм ге-нерирования:
r=U(0,1), если r<=p, X=1, иначе X=0, end.
2 Биномиальное распределение B(n,p). Случайная величина X имеет биноми-альное распределение с параметрами n, p (n=1,2,..; 0<=p<=1) если P(X=k)=n!/(k!*(n-k)!)*p^k*(1-p)^(n-k), k=0,1,..n. Упомянутая в п.1 величина B(p) является частным случаем, соответствующим n=1: B(p)=B(1,p). Алгоритм ге-нерирования:
X=0; для i =1,..,n, r=U(0,1), если r<=p, X=X+r, end.
3 Распределение Пуассона P(L). Случайная величина X имеет распределение Пуассона с параметром L (L>=0) если P(X=k)=exp(-L)*(L^k)/(k!), k=0,1,... Алго-ритм генерирования:
X=0; r=U(0,1); пока r>exp(-L), r=r*U(0,1), X=X+1, end.
4 Дискретное распределение Discr(N, P). Случайная величина X имеет дис-кретное распределение с параметрами N =[n(1), n(2),..n(m)],
P =[p(1),p(2),..,p(m)], (p(1)`+p(2)+..+p(m)=1, p(i)>0), если P(X=N(k))=p(k), k=0,1,..,m.Алгоритм генерирования:
M=U(0,1); i=1; пока M>0, M=M-p(i), i=i+1, end. X=n(i-1).
5 Дискретное равномерное распределение U(a,b). Случайная величина X имеет дискретное равномерное распределение с параметрами a,b (a<b целые числа) если P(X=i)=1/(b-a+1), i=a,..,b. Алгоритм генерирования:
M=U(0,1); X=целая_часть((b-a+1)*M)+a.
6 Геометрическое распределение G(p). Случайная величина X имеет геометри-ческое распределение с параметром p (0<=p<=1) если P(X=k)=p*(1-p)^(k-1), k=0,1,..,... Алгоритм генерирования:
M=U(0,1); X=целая_часть((ln(M)-ln(p))/ln(1-p))+1.
Непрерывные распределения.
1. Экспоненциальное распределение Exp(b). Случайная величина X имеет экс-поненциальное распределение Бернулли с параметром b (b>0), если ее плот-ность распределения 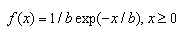 . Алгоритм генерирования: см. До-полнение 1.4.
. Алгоритм генерирования: см. До-полнение 1.4.
2. Распределение Эрланга Erl(b,m). Случайная величина X имеет распределе-ние Эрланга с параметрами L, m (L>0,m=1,2,..) если ее плотность распределе-ния 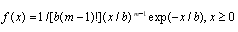 . Экспоненциальное распределение Exp(b), упомянутое в предыдущем пункте, является частным случаем Erl(b,1)=Exp(b).Алгоритм генерирования:
. Экспоненциальное распределение Exp(b), упомянутое в предыдущем пункте, является частным случаем Erl(b,1)=Exp(b).Алгоритм генерирования:
V=1; для i =1,..,m, r=U(0,1), V=V*r, end; X=-b*ln(V).
3. Нормальное распределение N(a, ). Случайная величина X имеет нормальное распределение с параметрами a, ( >0) если ее плотность распределения 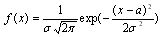
Алгоритм генерирования: см. Дополнение 1.5.
4. Распределение Стьюдента t(m). Случайная величина X имеет распределение Стьюдента с параметром m (m=1,2,..) если ее плотность распределения 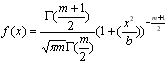 . Алгоритм генерирования:
. Алгоритм генерирования:
V=0; для i =1,..,m, r=N(0,1), V=V+r*r, end; r=N(0,1); X=r/sqrt(V).
5. Распределение хи-квадрат . Случайная величина X имеет распределе-ние хи-квадрат параметром m (m=1,2,..) если ее плотность распределения 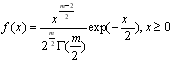 . Алгоритм генерирования:
. Алгоритм генерирования:
для m - четного V=1; для i =1,..,m/2, r=U(0,1), V=V*r, end; X=-1/2*ln(V).
для m - нечетного V=1; для i =1,..,(m-1)/2, r=U(0,1), V=V*r, end; r=N(0,1);
X=r*r+1/2*ln(V).
6. Распределение Епанечникова Ep. Случайная величина X имеет распределе-ние Епанечникова, если ее плотность распределения 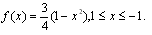 Ал-горитм генерирования:
Ал-горитм генерирования:
Шаг 1. Многократно генерировать X подчиненную равномерному зако-ну на [-1,1] и независящую от нее U, равномерно распределенную на [0,1], пока не окажется
U<=1-X^2.
Шаг 2. Вывести X.
НазадОглавление Вперед
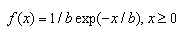 . Алгоритм генерирования: см. До-полнение 1.4.
. Алгоритм генерирования: см. До-полнение 1.4.
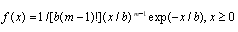 . Экспоненциальное распределение Exp(b), упомянутое в предыдущем пункте, является частным случаем Erl(b,1)=Exp(b).Алгоритм генерирования:
. Экспоненциальное распределение Exp(b), упомянутое в предыдущем пункте, является частным случаем Erl(b,1)=Exp(b).Алгоритм генерирования:
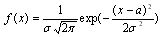
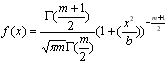 . Алгоритм генерирования:
. Алгоритм генерирования:
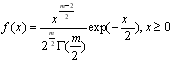 . Алгоритм генерирования:
. Алгоритм генерирования:
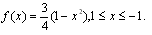 Ал-горитм генерирования:
Ал-горитм генерирования: