Схема устройства функции шифрования f показана на рис.3. Для вычисления значения функции f используются функция расширения Е, восьмиблоковое преобразование S, функция Р перестановки битов и цикловые ключи К_i. Опишем эти вспомогательные функции, а также метод генерирования цикловых ключей.

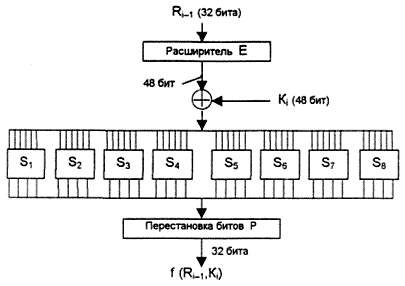Рис. 3. Схема вычисления функции шифрования f

Функция E, выполняющая расширение 32 бит ключа до 48 бит, определена в таблице 4. В соответствии с таблицей 4 первые три бита E(R_i-1) это биты 32, 1 и 2, а последние – 31, 32 и 1. Полученный результат (обозначим его E(R_i?1)) складывается по модулю 2 (операция XOR) с текущим значением ключа К_i и затем разбивается на восемь 6-битовых блоков B₁, B₂,... B₈:

E(R_i-1) + К_i = B₁, B₂,..., B₈.

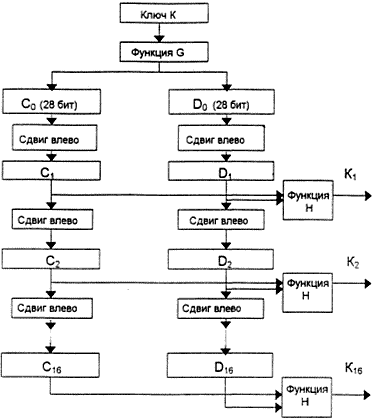Рис. 4. Схема вычисления ключей Кi

Далее каждый из этих блоков используется как номер элемента в функциях-матрицах S₁, S₂,..., S₈, содержащих 4-битовые значения (таблица 5). Эти блоки составляют восьмиблоковое преобразование S. Опишем способ выбора элемента в матрице S_j. Пусть на вход матрицы S_j поступает 6-ти битовый блок B_j=b₁b₂b₃b₄b₅b₆, тогда 2-битовый блок b₁b₆ указывает номер строки матрицы, а 4-битовое число b₂b₃b₄b₅ – номер столбца. Совокупность 6-битовых блоков B₁, B₂,... B₈ обеспечивает выбор 4-битового элемента в каждой из матриц S₁, S₂,..., S₈. В результате получаем 32-битовый блок: S₁(B₁)S₂(B₂)S₃(B₃)S₄(B₄)S₅(B₅)S₆(B₆)S₇(B₇)S₈(B₈). Этот блок преобразуется с помощью функции перестановки битов Р (табл.6). Таким образом, функция шифрования f по следующей формуле: f(R_i-1, K_i)=Р(S₁(B₁), ..., S₈(B₈)).

На каждой итерации алгоритма используется новое значение 48-битового ключа K_i. Текущее значение ключа K_i вычисляется по начальному ключу К (рис. 4). Ключ К представляет собой 64-битовый блок с 8 битами контроля по четности, расположенными в позициях 8, 16, 24, 32, 40, 56, 64. Для удаления контрольных битов и подготовки ключа к работе используется функция G первоначальной подготовки ключа (табл. 7).

Таблица 5

Функции преобразования S₁, S₂,..., S₈.

Таблица 7 разделена на две части. Результат преобразования G(K) разбивается на две половины C₀ и D₀ по 28 бит каждая. Первые четыре строки матрицы G определяют, как выбираются биты последовательности C₀ (первым битом C₀ будет бит 57 ключа шифра, затем бит 49 и так далее, а последними битами – бит 44 и 36 ключа).

Следующие четыре строки матрицы G определяют, как выбираются биты последовательности D₀ (т.е. последовательность D₀ будет состоять из битов 63, 55, 47, …, 12, 4 ключа шифра). Из таблицы 7 видно, что для генерации последовательностей C₀ и D₀ не используются биты 8, 16, 24, 32, 40, 48, 56 и 64 ключа шифра. Эти биты не влияют на шифрование и могут служить для других целей, например, для контроля по четности. Таким образом, в действительности ключ шифра является 56-битовым.

После определения C₀ и D₀ рекурсивно определяются C_i и D_i, i = 1, 2, …, 16. Для этого применяются операции циклического сдвига влево на один или два бита в зависимости от номера шага итерации, как показано в табл. 8.

Таблица 8.

Таблица сдвигов s_i для вычисления ключа.

Цикловый ключ К_i определяется по формуле К_i=H(C_iD_i), где функция Н задается матрицей (табл. 9).