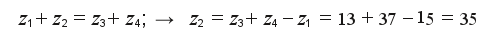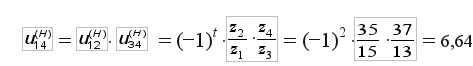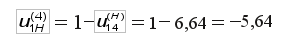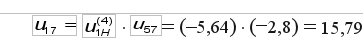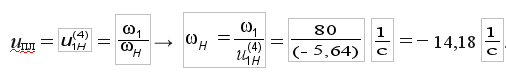|
Контрольная работа №1
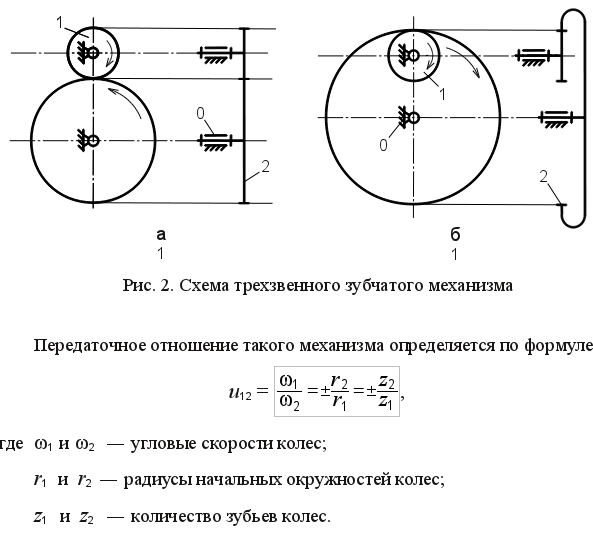
Задача 2 Краткие теоретические сведения Простейший плоский зубчатый механизм образуют два цилиндрических колеса, находящихся в зацеплении (рис. 2)
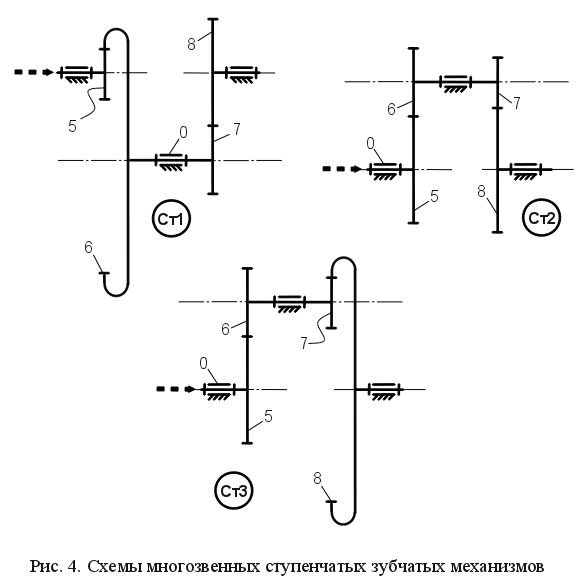
Знак "-" указывает на противоположное направление вращения колес, что соответствует внешнему зацеплению (рис. 2, а). Знак "+" указывает на одинаковое направление вращения колес, что соответствует внутреннему зацеплению (рис. 2, б). Плоские цилиндрические зубчатые механизмы подразделяются на механизмы с неподвижными осями вращения колес и на механизмы, имеющие колеса, оси вращения которых подвижны. Механизмы с неподвижными осями вращения колес подразделяются на рядовые (рис. 3) и ступенчатые (рис. 4). Передаточное отношение таких механизмов определяется произведением передаточных отношений пар колес, находящихся в зацеплении и вычисляется по формулам:
Планетарным механизмом называется зубчато–рычажный механизм с подвижными осями вращения некоторых колес (рис. 5). Звено, на котором располагаются подвижные оси зубчатых колес называется водилом (Н), а колеса с подвижными осями вращения – сателлитами или планетарными колесами (2, 3). Колеса с неподвижными осями вращения называются солнечными или центральными (1) , неподвижное колесо называется опорным (4).
Верхний индекс в скобках указывает неподвижное звено (т.е. звено, являющееся стойкой). Передаточное отношение
Рис.5 Схемы планетарных механизмов всем звеньям планетарного механизма угловой скорости Оси вращения центрального колеса 1 и водила Н располагаются вдоль одной прямой, сателлиты 2 и 3`также имеют общую ось вращения. Условие соосности записывается в виде равенств для начальных окружностей или (если модули всех колес одинаковы) чисел зубьев колес:
При определении угловой скорости сателлитов планетарных механизмов используются формула:
Задание Определить передаточные отношения зубчатого редуктора, считая входным вал колеса 1, и угловые скорости всех зубчатых колес.
Исходные данные Вариант общей схемы механизма задается схемами, приведенными на рисунках 3 или 4 и 5, и представляет собой их последовательное соединение, а также номерами вариантов данных, приведенных в табл. 4, 5, 6 и 7. Задание Пример выполнения Пусть необходимо выполнить вариант, заданный в виде последовательности схем:
Общее передаточное отношение такого механизма определяется произведением передаточного отношения планетарного механизма (см. форм. 3) и рядового (см. форм. 1):
Пусть вариант чисел зубьев колес будет таким: z1=15; z3=13; z4=37; z5=15; z6=27; z7=42, угловая скорость
Далее необходимо определить z2 из условия соосности:
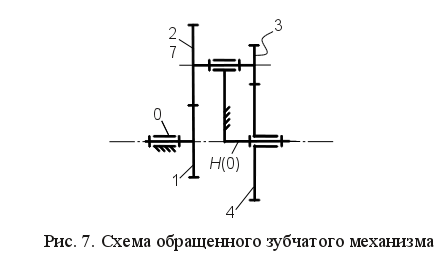
затем передаточное отношение обращенного механизма (см. рис. 7):
затем передаточное отношение планетарного механизма:
и передаточное отношение рядового механизма:
Общее передаточное отношение механизма равно:
Теперь можно определить угловые скорости всех колес. Угловая скорость водила определяется следующим образом:
Для определения угловой скорости сателлитов используется форм. (4):
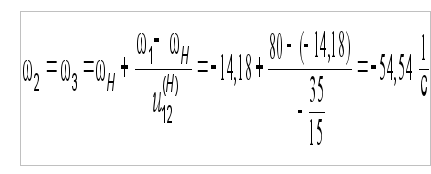
Затем определяются угловые скорости остальных колес:
|



 называют передаточным отношением обращенного механизма, т.е. механизма, полученного сообщением
называют передаточным отношением обращенного механизма, т.е. механизма, полученного сообщением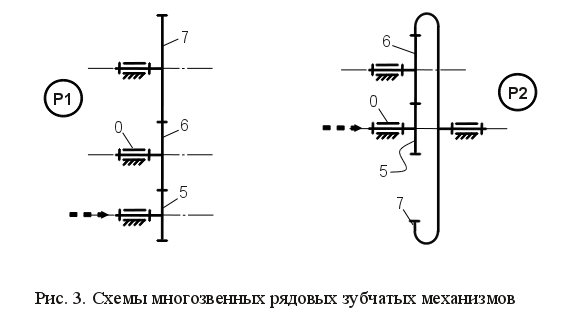
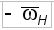 Такой прием называется методом обращения движения. При этом опорное колесо становится подвижным, а водило – неподвижным. В результате получается ступенчатый механизм с неподвижными осями вращения всех колес. Для схемы
Такой прием называется методом обращения движения. При этом опорное колесо становится подвижным, а водило – неподвижным. В результате получается ступенчатый механизм с неподвижными осями вращения всех колес. Для схемы  бращенный механизм получается рядовой и формула, определяющая его передаточное отношение упрощается:
бращенный механизм получается рядовой и формула, определяющая его передаточное отношение упрощается:
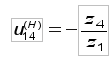
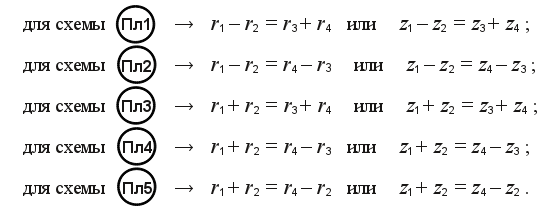
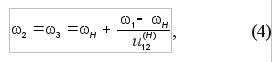
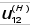 - передаточное отношение ступени обращенного механизма, т.е. при неподвижных осях вращения колес
- передаточное отношение ступени обращенного механизма, т.е. при неподвижных осях вращения колес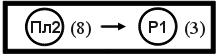 расшифровывается следующим образом: последовательно соединяются схемы механизмов, которые показаны на рис. 3 и 5 (общий вал указан пунктирными стрелками), данные для расчетов берутся из табл. 6 и 4 в соответствии с номером варианта, указанного в скобках.
расшифровывается следующим образом: последовательно соединяются схемы механизмов, которые показаны на рис. 3 и 5 (общий вал указан пунктирными стрелками), данные для расчетов берутся из табл. 6 и 4 в соответствии с номером варианта, указанного в скобках.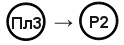 .Схема механизма в этом случае выглядит так, как показано на рис. 6.
.Схема механизма в этом случае выглядит так, как показано на рис. 6. 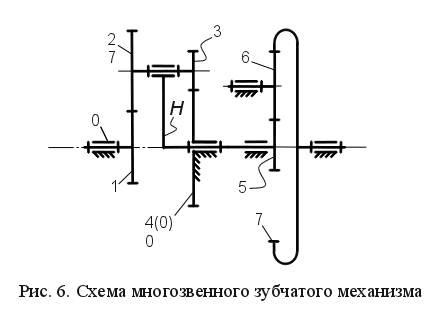
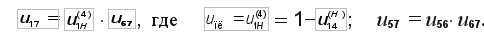
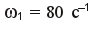 Схема обращенного зубчатого механизма представлена на рис. 7.
Схема обращенного зубчатого механизма представлена на рис. 7.