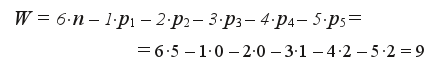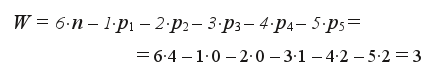|
Контрольная работа №1
Контрольная работа состоит из двух заданий. В первом задании проводится структурный анализ схемы пространственного механизма манипулятора промышленного работа, во второй – проводится кинематический анализ сложного зубчатого механизма. Задача 1 Краткие теоретические сведения Кинематической цепью называется система звеньев, образующих кинематические пары.
Число степеней свободы (подвижность) пространственного механизма определяется по формуле Сомова - Малышева:
В соответствии с классификацией по И.И. Артоболевскому все кинематические пары подразделяются на пары 1, 2, 3, 4 и 5-го классов. Класс пары определяется числом условий связи S (см. табл. 1) в относительном движении звеньев. В соответствии с классификацией по Ф. Рело все кинематические пары подразделяются на высшие и низшие. Высшей называется пара, в которой требуемое относительное движение звеньев может быть обеспечено соприкосновением элементов, образующих пару, по линии или в точке (табл.1: плоскость - шар, плоскость - цилиндр); низшей в которой это может быть обеспечено соприкосновением по поверхностям (табл.1: плоскостная, сферическая, цилиндрическая, сферическая с пальцем, вращательная, поступательная). Таблица 1. Примеры кинематических пар Число степеней свободы (подвижность) плоского механизма определяется по формуле Чебышева:
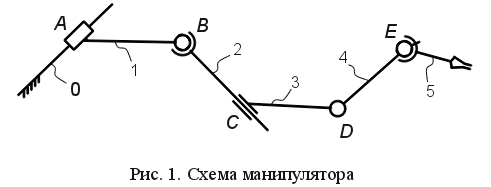
Под маневренностью манипулятора понимается его число степеней свободы при неподвижном захвате. При определении маневренности необходимо учитывать, что в этом случае манипулятор превращается в механизм с замкнутой кинематической цепью. Чем выше маневренность, тем совершеннее манипулятор. Задание Определить число степеней свободы и маневренность механизма манипулятора. Исходные данные Вариант схемы механизма задается элементами, приведенными в табл. 2 и 3, и представляет собой их последовательное соединение. Например, задание Пример выполнения Пусть задан вариант в виде следующей последовательности звеньев
Получившийся механизм является пространственным, поэтому для определения подвижности применяется формула Сомова – Малышева. Манипулятор имеет пять подвижных звеньев, одну кинематическую пару третьего класса (сферическая пара В), две – четвертого класса (цилиндрическая пара С и сферическая с пальцем пара E) и две – пятого класса (поступательная пара А и вращательная пара D), следовательно:
При неподвижном захвате механизм остается пространственным, количество подвижных звеньев уменьшается (n = 4), а количество и виды кинематических пар не изменяются. Следовательно, маневренность определяется следующим образом:
|

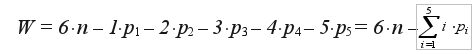 ,
,
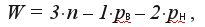
 расшифровывается следующим образом: из табл. 3 выбирается вариант стойки, затем из табл. 2 выбираются варианты промежуточных подвижных звеньев выходного звена.
расшифровывается следующим образом: из табл. 3 выбирается вариант стойки, затем из табл. 2 выбираются варианты промежуточных подвижных звеньев выходного звена. Схема механизма в этом случае выглядит так, как показано на рис. 1.
Схема механизма в этом случае выглядит так, как показано на рис. 1.