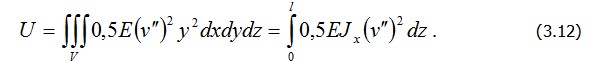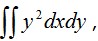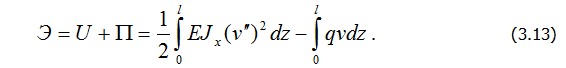|
3.2. Энергия деформируемого тела как функционал
Под функционалом понимается скалярная величина, зависящая от некоторой функции или нескольких функций как от аргументов. Она определяется выбором функций-аргументов из некоторого заданного класса, совместимых с условиями задачи. Функционал можно трактовать как функцию, зависящую от бесконечного числа аргументов. Эти аргументы оказываются заданными, как только выбраны функции-аргументы.
В разделе математики, называемом вариационное исчисление, изучаются условия, при которых функционалы обладают свойством локальной экстремальности (стационарности), т.е. при произвольном бесконечно малом изменении функций-аргументов значение функционала не изменяется. Такие функции-аргументы, при которых функционал стационарен, называются экстремалями данного функционала.
Напомним сначала некоторые классические задачи об отыскании экстремалей функционалов.
На рис. 3.1, а заштрихована площадь А, которую охватывает кривая y(x) , имеющая фиксированную длину L между точками В и С. Функционал
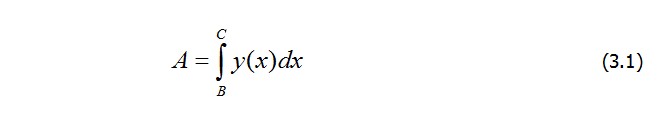
имеет максимум, если кривая y(x) очерчена по окружности, т.е. из всех кривых длиной L, проходящих через точки В и С, экстремалью является часть окружности длиной L. Решение этой задачи было известно еще в древности.
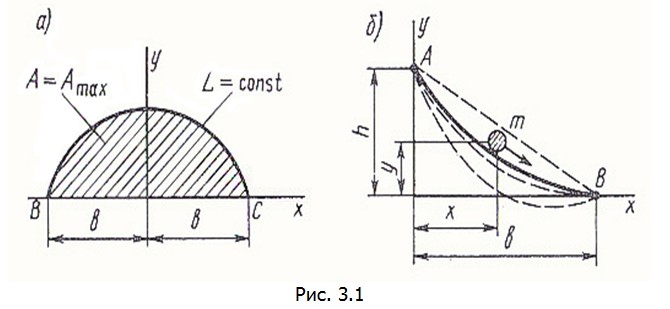
На рис. 3.1, б изображена схема другой известной задачи о так называемой брахистохроне – кривой y(x) , обеспечивающей кратчайшее время соскальзывания под действием силы тяжести точечной массы m (без трения) из точки А в точку В. Вертикальная скорость массы 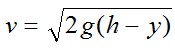 ,поэтому ее горизонтальная скорость будет ,поэтому ее горизонтальная скорость будет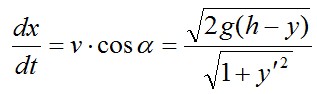 .Отсюда найдем и время движения .Отсюда найдем и время движения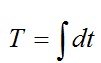 в виде функционала, зависящего от кривой y(x) в виде функционала, зависящего от кривой y(x)
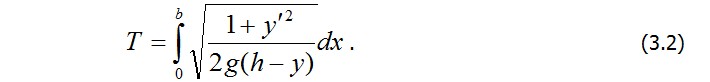
Эта задача, поставленная еще Г. Галилеем, была решена различными методами Я. Бернулли, Г.Лейбницем, И. Ньютоном и др. Экстремалью в данном случае является циклоида, образованная качением круга по горизонтальной прямой y=h. Радиус этого круга зависит от Радиус этого круга зависит от отношения 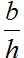 Интересно, что при Интересно, что при 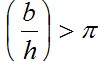 кривая наискорейшего спуска проходит частично несколько ниже оси x (нижняя пунктирная линия на рис. 3.1,б). кривая наискорейшего спуска проходит частично несколько ниже оси x (нижняя пунктирная линия на рис. 3.1,б).
Обратимся теперь к функционалу, имеющему важное значение в механике твердого тела, - функционалу, выражающему полную потенциальную энергию деформированного тела и действующей на него нагрузки (рис. 3.2, б). Полная энергия Э состоит из потенциальной энергии деформации тела (потенциал внутренних сил) U и энергии внешних сил (потенциал внешних сил) П :
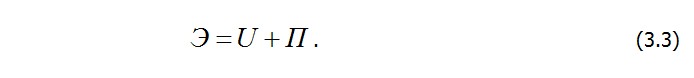
Условно будем считать, что в начальном недеформированном состоянии Э0(рис. 3.2, а) Следовательно, полная энергия Э представляет собой изменение энергии внутренних и внешних сил при переходе тела из начального в деформированное состояние.
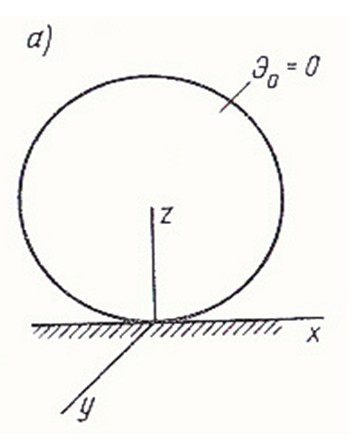 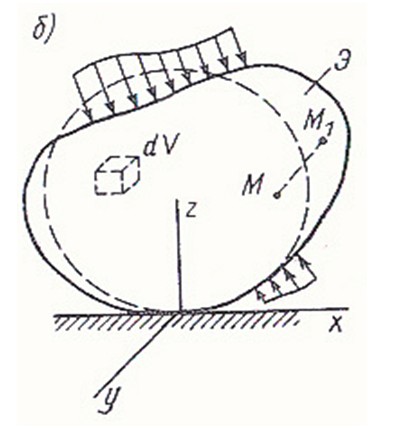 
Энергия любой системы сил измеряется работой, которую могут совершить эти силы при переводе системы из рассматриваемого состояния в начальное, нулевое, состояние, где принято Э0=0.Поэтому при составлении выражения (3.3) будем вычислять энергию как работу внутренних сил упругости (для U ) и внешних сил (для П ) при мысленном переводе тела из деформированного в начальное недеформированное состояние.
Составим вначале выражение для потенциала внутренних сил U . Так как деформации по объему тела распределены неравномерно, то и энергия деформации в объеме тела распределена так же неравномерно. Введем понятие плотности энергии деформации U0 или удельной потенциальной энергии деформации согласно выражению

Оно показывает, что U0– это предел отношения энергии ΔU накопленной в объеме ΔV, к объему ΔV , стремящемуся к нулю. Для однородного деформированного состояния U0 выражает энергию, накопленную в единице объема материала.
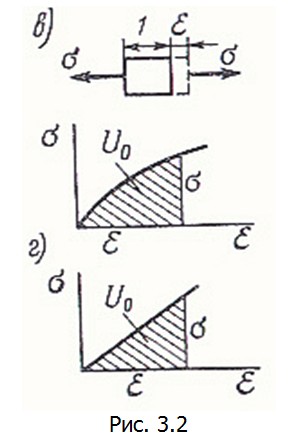
В случае линейного напряженного состояния плотность энергии деформации выражается площадью диаграммы деформирования материала (рис. 3.2, в – нелинейно-упругий материал, рис. 3.2, г – линейно-упругий). В последнем случае U0=0,5δεОбобщая эту формулу на случай объемного напряженного состояния, получим
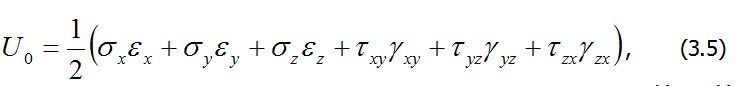
или в сокращенной форме, используя обозначения векторов
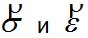 [(2.5), (2.15)], запишем (3.5) в виде
[(2.5), (2.15)], запишем (3.5) в виде

Во всем объеме V энергию деформации U найдем путем интегрирования по объему:
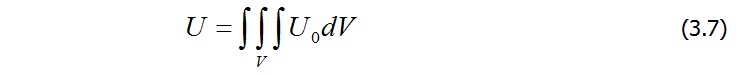
Подчеркнем, что при вычислении U 0как работы следует вычислять работу именно внутренних напряжений σ' в отличие от напряжений σ , приложенных к граням кубика материала и являющихся для него внешним воздействием (рис. 3.3). На рисунке показано,
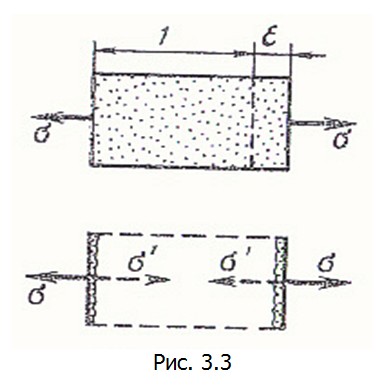 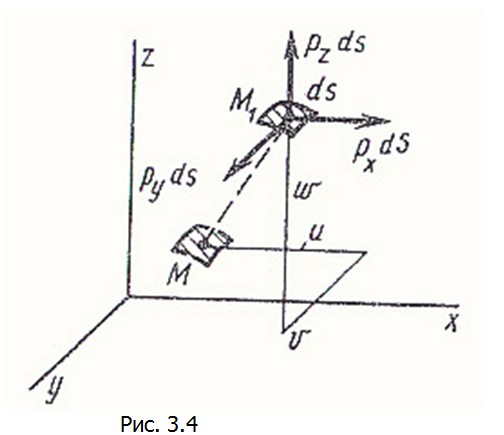
что материал элемента условно удален и заменен внутренними («стягивающими») напряжениями σ'При уменьшении деформации от εдо нуля напряжение σ'совершает положительную работу, равную U0.Вообще, упругие силы, стремясь восстановить первоначальную форму деформированного тела, будут давать положительную энергию деформации (3.7) и создавать положительный вклад в общий баланс энергии Э.составим выражение для потенциала внешних сил П . Будем считать, что значение этих сил не зависит от перемещения точки приложения силы (весовая нагрузка, давление жидкости или газа и т.п.). На рис. 3.4 показаны элементарные поверхностные силы pxdS, pydS,pzdS,действующие на площадку dS в деформированном состоянии.При переводе тела в недеформированное состояние точка M 1 перейдет в положение M и указанные силы совершат отрицательную работу на перемещениях, соответственно u, v, w.Следовательно,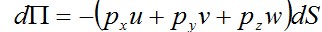 .Аналогично, для объемной нагрузки получим .Аналогично, для объемной нагрузки получим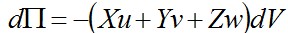 .Интегрируя по поверхности тела S и объему V , найдем потенциал внешних сил в виде .Интегрируя по поверхности тела S и объему V , найдем потенциал внешних сил в виде
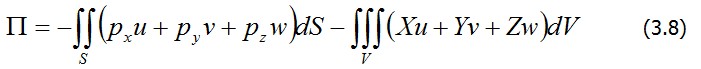
или в сокращеной векторной форме
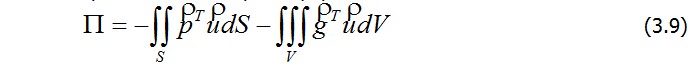
Легко видеть, что величина энергии U , так же как и П , вполне определяется заданием функций перемещений u , v и w. Действительно, используя закон Гука (2.24) и уравнения Коши (2.16), выражению (3.6) для U 0 можно придать вид
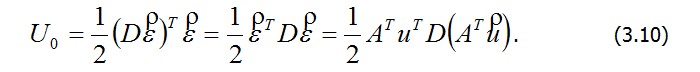
Следовательно, полная энергия тела (3.3) является функционалом, зависящим от выбора трех функций-аргументов
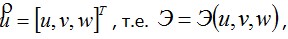
или в развернутой форме
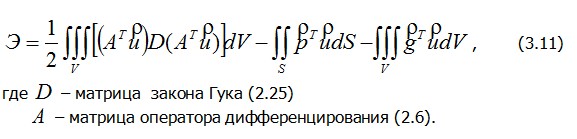
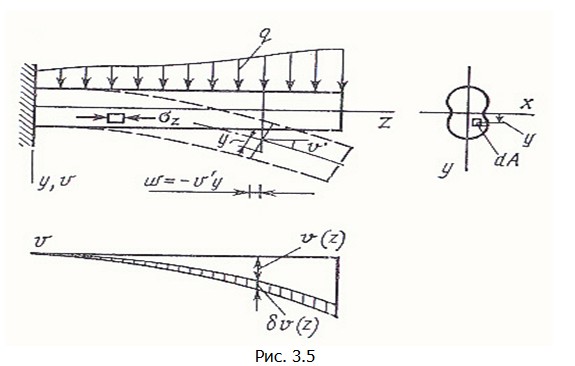
Приведем пример составления функционала (3.11). составим выражение полной энергии Э для балки (рис. 3.5), считая, как это делается обычно в сопротивлении материалов, справедливой гипотезу плоских сечений и пренебрегая влиянием на ее деформации напряжений σ y,σ x и касательных напряжений τ . Таким образом, при определении энергии упругой деформации U будем учитывать только напряжения σ z. В этом случае 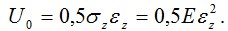 .Перемещение w точки сечения за счет его поворота на угол v' будет w=-v'y; следовательно .Перемещение w точки сечения за счет его поворота на угол v' будет w=-v'y; следовательно 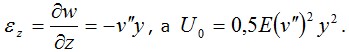 Здесь и далее штрихом отмечаем дифференцирование по Z . Интегрируя по объему балки, найдем Здесь и далее штрихом отмечаем дифференцирование по Z . Интегрируя по объему балки, найдем
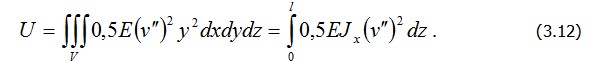
В выражении для U интеграл 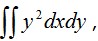
вычисляемый по площади сечения A, заменен на момент инерции этого сечения Jx.
Потенциал нагрузки q найдем в виде 
Окончательно функционал полной энергии (3.12) получит вид
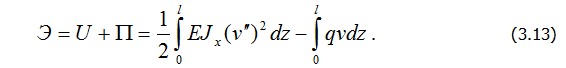
Далее ->
|



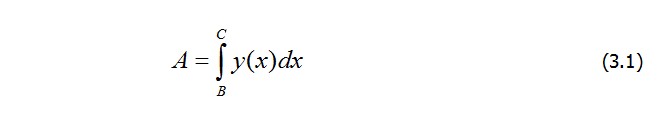

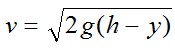 ,поэтому ее горизонтальная скорость будет
,поэтому ее горизонтальная скорость будет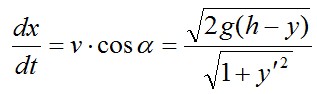 .Отсюда найдем и время движения
.Отсюда найдем и время движения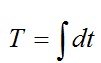 в виде функционала, зависящего от кривой y(x)
в виде функционала, зависящего от кривой y(x)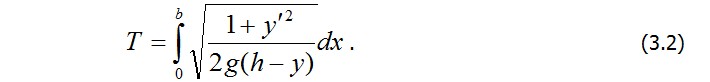
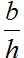 Интересно, что при
Интересно, что при 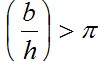 кривая наискорейшего спуска проходит частично несколько ниже оси x (нижняя пунктирная линия на рис. 3.1,б).
кривая наискорейшего спуска проходит частично несколько ниже оси x (нижняя пунктирная линия на рис. 3.1,б).
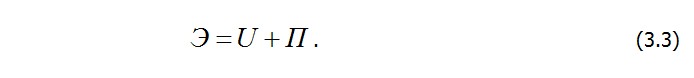




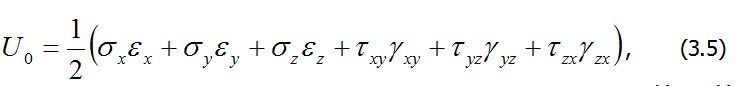
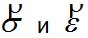 [(2.5), (2.15)], запишем (3.5) в виде
[(2.5), (2.15)], запишем (3.5) в виде 
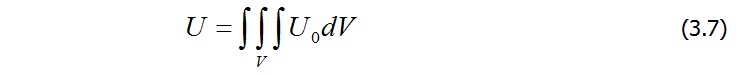


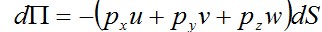 .Аналогично, для объемной нагрузки получим
.Аналогично, для объемной нагрузки получим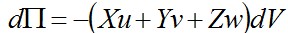 .Интегрируя по поверхности тела S и объему V , найдем потенциал внешних сил в виде
.Интегрируя по поверхности тела S и объему V , найдем потенциал внешних сил в виде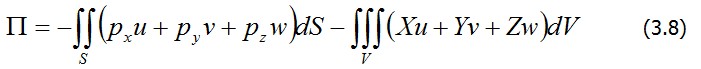
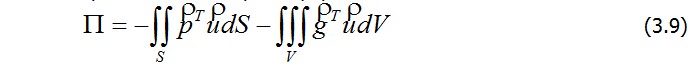
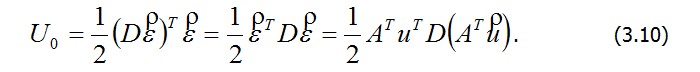
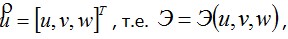
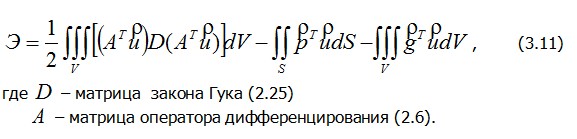

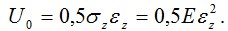 .Перемещение w точки сечения за счет его поворота на угол v' будет w=-v'y; следовательно
.Перемещение w точки сечения за счет его поворота на угол v' будет w=-v'y; следовательно 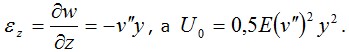 Здесь и далее штрихом отмечаем дифференцирование по Z . Интегрируя по объему балки, найдем
Здесь и далее штрихом отмечаем дифференцирование по Z . Интегрируя по объему балки, найдем