1.ГРАДИЕНТНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
ЗАДАЧА №1 ([3], стр.193).
Найти наименьшую длину
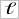изгороди, с помощью которой можно огородить участок в форме прямоугольника площадью S, примыкающий к стенке (рис.1).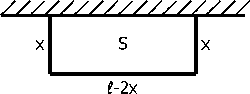
Учитывая принятые обозначения, площадь ограждения можно представить как
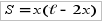, откуда 
.
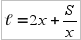Решение задачи сводится к определению наименьшего значения этой функции при изменении x от 0 до ∞. При x→0 и при x→∞ функция
.
Следовательно, наименьшее значение следует искать среди минимумов функции в интервале (0,∞). Возьмём производную 
.
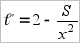В интересующем нас интервале имеем одну стационарную точку:
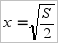(при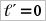 
), которая является точкой минимума функции
(т.к.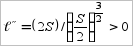 
), ибо 
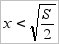, если 
, и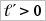 
, если 
.
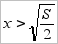Минимальное значение
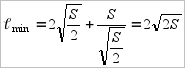здесь служит и наименьшим значением функции во всём интервале (0,∞).
Значит, какой бы забор, огораживающий прямоугольный участок с площадью S и примыкающий к стене, мы ни взяли, его длина не может быть меньше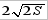 
и равна этому значению только в том случае, когда меньшая сторона прямоугольника (равная 
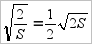) в два раза меньше его большей стороны (равной 
).
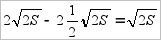В указанных условиях самый экономичный забор тот, у которого большая сторона в два раза длиннее меньшей стороны.
ЗАДАЧА №2 ([4], стр.134).
Указать наилучший вариант консервной банки фиксированного объёма V, имеющей обычную форму прямого кругового цилиндра при: а)наименьшей поверхности S (наименьшем количестве жести); б)наименьшей длине сварных швов
.
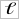Для решения задачи запишем формулы для объёма банки, площади её поверхности и длины швов:
Объём банки задан, что определяет связь между радиусом r и высотой h. Выразим высоту через радиус:
.
и подставим полученное выражение в формулы для поверхности и длины швов. В результате получим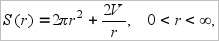 
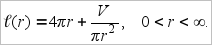
Таким образом задача сводится к определению такого значения r, при котором достигает своего наименьшего значения в одном случае функция
,
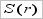в другом – функция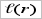 
.
Рассмотрим первый вариант задачи. Вычислим производную функции
:
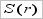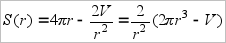
и исследуем её знак. При
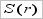производная отрицательна и функция убывает, при 
производная положительна и функция
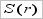возрастает. Следовательно, своего наименьшего значения эта функция достигает в точке 
,в которой её производная обращается в нуль. График функции
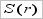,иллюстрирующий приведенный анализ, показан на рис.2.
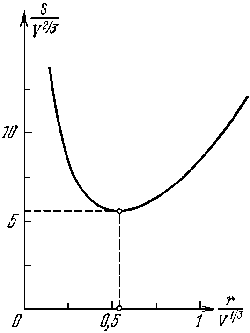
Итак, радиус и высота банки, наилучшие с точки зрения условия минимальности
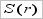, определяются формулами 
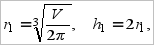при этом 
.
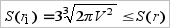Рассмотрим теперь задачу во второй постановке. Продифференцируем функцию
:
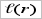.Как и в предыдущем случае, при
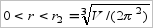производная отрицательна и функция 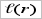убывает, при 
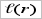производная положительна и функция возрастает. Следовательно, своего наименьшего значения эта функция достигает в точке 
,
в которой её производная обращается в нуль. График функции показан на рис.3.
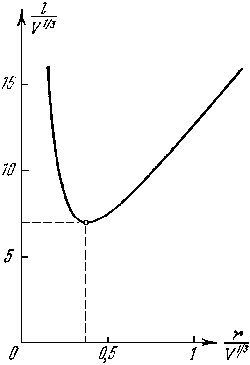
Итак, радиус и высота банки, наилучшие с точки зрения условия минимальности
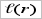, определяется формулами
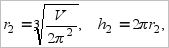, при этом 
.