|
Методика
выполнения работы
Программная реализация решения предлагаемой в примере задачи
может быть выполнена по алгоритму, блок-схема которого в
укрупнённом виде представлена на рис.2(а), а более подробно
рассмотрена на рис.2(б).
|
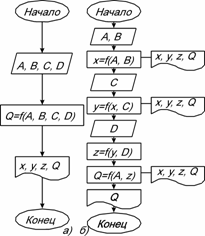
Рис.2 Укрупнённая (а) и подробная (б)
блок-схема алгоритма |
При выборе типа и параметров аппроксимирующих функций, входящих
в модель
Q=f(A,B,C,D),
последовательно, для каждого квадранта, рекомендуется
использовать редактор
электронных таблиц
MS
Excel, по методике, изложенной в
источниках [2] или ([3], С.:18-22) при R^2³0,95.
Для этого обобщённая искомая функция
Q
разделяется поквадрантно на взаимозависимые характеристики
x=f(A,B);
y=f(x,C);
z=f(y,D);
Q=f(z,A), соответственно.
Приводимая ниже программа ориентирована на диалоговый режим
работы с пользователем посредством интерактивного обмена
информацией, без сохранения на жёстком диске отчёта об
определяемых данных. В архитектуре программы предусмотрена
возможность многократного возврата к вводу исходных данных,
после определения параметра
Q, которая определена действием
команд, следующих после метки 996.
В архитектуре программы должна быть предусмотрена функция
проверки промежуточных расчётных данных их допустимым
интервалам, которые определяются в соответствие с исходными
данными используемой номограммы. К таким фрагментам архитектуры
могут быть отнесены, например, строки программы, находящиеся
после меток: 4, 18, 26, 27, 999. Аналогичным образом в программе
учитываются действительные диапазоны аргумента
y для функции
z в третьем квадранте, заданные
условиями, отмеченные
меткой 29 (4 строки).
Для четвёртого квадранта определение искомого параметра
Q
производится исходя из последовательного перебора всех графиков
функции. Так, для текущих значений А последовательно
рассчитываются все функции
z(Q)=f(A) (в программе
z(Q)Ûzz(k))
до тех пор, пока
z(Q)≥z, после чего значение
Q
определяется из пропорционального положения проекционной точки
между ближайшими графиками
Q(k-1)
и
Q(k).
При этом принято, что отсчёт графиков функций, изображённых на
квадранте
IV
определяется диапазоном значений
kÎ[2…8],
а при
k=1 предполагается, что
Q(1)=0,
т.е. совпадает с осью А (см. рис.1).
Program Primer
common Q(8), zz(8)
C Обработка первого квадранта
106 write (*,1)
1 Format ('Vvedite parametr A (0-10),F5.0')
Read (*,2) A
2 Format (F5.1)
11 write (*,3)
3 Format (1x,'Vvedite kod znacheniya parametra B iz
*ryada:',/,1x,'k=1 pri B=1,25',/,1x,'k=2 pri B=1,75'
*,/,1x,'k=3 pri B=2,25',/,1x,'k=4 pri B=2,75',/,1x,'
*k=5
pri
B=3,25')
Read (*,4)k
4 format (I1)
C Условие проверки соответствия вводимого номера гра
С фика k интервалу его допустимых значений
if
(k-5)10,10,11
10
if
(k)11,11,12
12 Goto (5,6,7,8,9) k
5
x=-7.875*A+73.875
goto 16
6
x=-7.875*A+83.875
goto 16
7 x=-7.875*A+93.875
goto 16
8 x=-7.875*A+103.88
goto 16
9 x=-7.875*A+113.88
16 Continue
write (*,200)x
200
format (F10.2)
C Обработка второго квадранта
14 write (*,17)
17 Format (1x,'Vvedite kod znacheniya parametra C iz
*riada:',/,1x,'l=1 pri C=17',/,1x,'l=2 pri C=22',/,
*1x,'l=3 pri C=31',/,1x,'l=4 pri C=42')
Read (*,18)l
18
format
(I1)
C Условие проверки соответствия вводимого номера гра
С фика l интервалу его допустимых значений
if (l-4)13,13,14
13 if (l)14,14,15
15 goto (20,21,22,23)l
20 y=-0.0043*x**2+0.2052*x+29.998
goto 28
21 y=-0.0031*x**2+0.1315*x+25.297
goto 28
22 y=-0.0018*x**2+0.0574*x+17.252
goto 28
23
y=-0.0009*x**2+0.0218*x+8.809
28
Continue
write (*,201)y
201 format (F10.2)
C Обработка третьего квадранта
24 write (*,25)
25 Format (1x,'Vvedite kod znacheniya parametra D iz
*riada:',/,1x,'m=1 pri D=1,2',/,1x,'m=2 pri D=1,6'
*,/,1x,'m=3 pri D=2,0',/,1x,'m=4 pri D=2,4',/,1x,'
*m=5
pri D=2,8')
Read (*,26)m
26 format (I1)
C Условие проверки соответствия вводимого номера гра
С фика m интервалу его допустимых значений
if (m-5)27,27,24
27 if (m)24,24,29
C Условие проверки соответствия значений
Y
значениям
С допустимых аргументов функций третьего квадранта
29 if (m.EQ.1.AND.y.LT.14)goto 989
if (m.EQ.2.AND.y.LT.10)goto 989
if (m.EQ.4.AND.y.GT.22)goto 989
if (m.EQ.5.AND.y.GT.18)goto 989
goto 990
989 write(*,988)
988 Format (1x,'Vvedite inoe m dlya D pri dannom y',/)
goto 24
990 goto (30,31,32,33,34)m
30 z=-0.2063*y**2+11.238*y-94.143
goto 35
31 z=-0.2017*y**2+11.384*y-87.188
goto 35
32 z=3.3333*y
goto 35
33 z=0.1974*y**2-1.4014*y+34.609
goto 35
34 z=0.2161*y**2-1.7819*y+49.963
35 Continue
write (*,202)z
202 format (F10.2)
C Обработка четвёртого квадранта
Q(2)=0.4
Q(3)=0.63
Q(4)=1.0
Q(5)=1.6
Q(6)=2.5
Q(7)=4.0
Q(8)=6.3
i=0
Q(1)=0
zz(1)=0
do 100 k=2,8
if (i.EQ.1) goto 100
nn=k-1
zz(k)=-5*A+nn*10+30
if (zz(k).GE.z) goto 221
goto 222
221 i=1
goto 223
222 i=0
goto 999
223 delzz=ABS(zz(k)-zz(nn))
delz=z-zz(nn)
QQ=(delz/delzz)*(Q(k)-Q(nn))+Q(nn)
999 Continue
if (i.EQ.0.AND.k.EQ.8) goto 998
goto 100
998 write (*,997)
997 Format (1x,'Net deistvitelnyh znacheniy Q dlia
*vybrannyh parametrov A i z')
100 Continue
ii=i+1
goto (996, 995)ii
995 write (*,101)QQ,z
101 Format (1x,'Q=',F10.2,/,1x,'z=',F10.1)
996 write (*,102)
102 format (1x,'Zavershit raschet:1-da;0-net')
read (*,103)ll
103 format (I1)
lll=ll+1
goto (106,104)lll
104 continue
end
В представленном выше листинге программы используются
стандартные, для алгоритмического языка
Fortran,
обозначения, которые приводятся в табл.1. Также, в соответствие
с правилами, действующими по умолчанию, обозначение переменных
целого типа в программе должно начинаться с литер i,j,k,l,m,n и не превышать 8 знаков. Остальные
переменные, если их тип не определён специальными командами,
считаются вещественными (при вводе значений для них следует
после целой части ставить точку независимо от наличия дробной
составляющей).
|
Условные обозначения. Таблица 1
|
Обозн. |
Операция |
|
+ |
Сложение |
|
- |
Вычитание |
|
* |
Умножение |
|
/ |
Деление |
|
** |
Возведение в степень |
|
.LT. |
Меньше |
|
.LE. |
Меньше или равно |
|
.GT. |
Больше |
|
.GE. |
Больше или равно |
|
.EQ. |
Равно |
|
.NE. |
Не равно |
|
.AND. |
И |
|
|
