СИЛОВОЙ  АНАЛИЗ  МЕХАНИЗМА

            Целью силового анализа является исследование движения механизма с учетом сил, действующих на его звенья.
Задачами силового анализа являются:
1. Определение сил, действующих на звенья механизма.
2. Определение реакций в кинематических парах.
3. Определение уравновешивающей силы (момента), приложенной к ведущему звену.

            Силовой анализ механизма основан на известном из теоретической механики принципе Даламбера. Суть этого принципа применительно к задачам силового анализа сводится к тому, что если к звену механизма помимо реальных сил приложить фиктивные силы инерции, то его можно рассматривать условно находящимся в равновесии и для определении неизвестных параметров реакций в кинематических парах можно использовать уравнения статики. Поэтому этот метод силового анализа называется методом кинетостатики.

1. Силы инерции  звеньев механизмов

            Из теоретической механики известно, что в общем случае плоского движения распределенные по всему звену элементарные силы инерции можно привести к равнодействующей  и к паре сил с моментом  .
Значение силы инерции звена определяется по формуле
,
где      m – масса звена;
 - ускорение центра масс звена.
Момент пары сил инерции относительно оси, проходящей через его центр масс равен
,
где       - момент инерции звена относительно центра масс;
 - угловое ускорение звена.
Знак минус в формулах показывает, что сила Pu направлена противоположно ускорению , момент      - противоположно угловому ускорению звена.
Наличие Pu,  или одновременно обоих зависит от характера движения звена. Рассмотрим основные виды движения звеньев: поступательное, плоскопараллельное, вращательное.
1. Звено совершает поступательное движение:

.
2. Звено совершает плоскопараллельное движение:

.
3. Звено совершает вращательное движение:
а)

;
б) Если звено вращается с постоянной угловой скоростью, то

.
Ускорения центров масс и угловые ускорения определяются по плану ускорений.
Для проведения силового анализа кинематическая цепь должна быть статически определимой.
Статически определимой считается цепь, у которой число известных параметров реакций равно количеству уравнений статики, которые можно составить для их определения.
Каждая реакция характеризуется 3-мя параметрами: величиной, направлением и точкой приложения.
Кинематические пары 5-го класса имеют два неизвестных параметра реакции:
вращательная пара:

не известны: величина и направление;
известна: точка приложения (центр шарнира);
поступательная пара:

не известны: величина и точка приложения;
известно: направление (перпендикулярно к направляющей).
Условие статической неопределимости плоской кинематической цепи выражается уравнением
.
Это условие совпадает с условием существования структурной группы, поэтому структурные группы являются статически определимыми цепями.
Отдельное звено и весь механизм в целом являются статически неопределимыми. Статическая неопределимость в механизм вносится механизмом 1-го класса.
Для того, чтобы механизм 1-го класса стал статически определимым, к нему необходимо приложить уравновешивающую силу или уравновешивающий момент.
Уравновешивающая сила (момент) – это реальная сила (момент), приложенная со стороны двигателя, и которая уравновешивает все силы, действующие на звенья, включая силы инерции и моменты пар сил инерции.
Точка приложения и направление уравновешивающей силы (момента) всегда известны и определяются конструкцией передаточного механизма, используемого для передачи движения от двигателя к ведущему звену (в курсовой работе принять направление  перпендикулярно кривошипу).
Уравновешивающая сила (момент) определяется в результате силового анализа механизма 1-го класса.
Уравновешивающую силу (момент) можно определить с помощью метода Жуковского (этот метод изложен дальше).

2. Последовательность проведения силового анализа

            1. Выбирается положение для исследования и строится для него план скоростей и план ускорений.
2. Определяются силы инерции и моменты пар сил инерции звеньев.
3. Определяется сила сопротивления, действующая на рабочее звено механизма по диаграмме сил сопротивления.
4. Проводится силовой расчет групп и определяются реакции в кинематических парах (силовой анализ начинается с наиболее удаленной группы от ведущего звена и проводится в порядке обратном формуле строения механизма).
5. Проводится силовой анализ механизма 1-го класса и определяется уравновешивающая сила или уравновешивающий момент.
6. Определяется уравновешивающая сила или уравновешивающий момент по методу Н.Е.Жуковского.
7. Определяется погрешность расчета уравновешивающей силы или уравновешивающего момента обоими методами, при этом метод Жуковского принимается как более точный.
Пример: Силовой анализ проведен на примере механизма, для которого проводился кинематический анализ (рис.4).
Исходные данные: Сила сопротивления, действующая на ползун 5  (в заданиях на курсовой проект она определяется по диаграмме сил сопротивления). Веса звеньев: ,  , , . Моменты инерции: , .

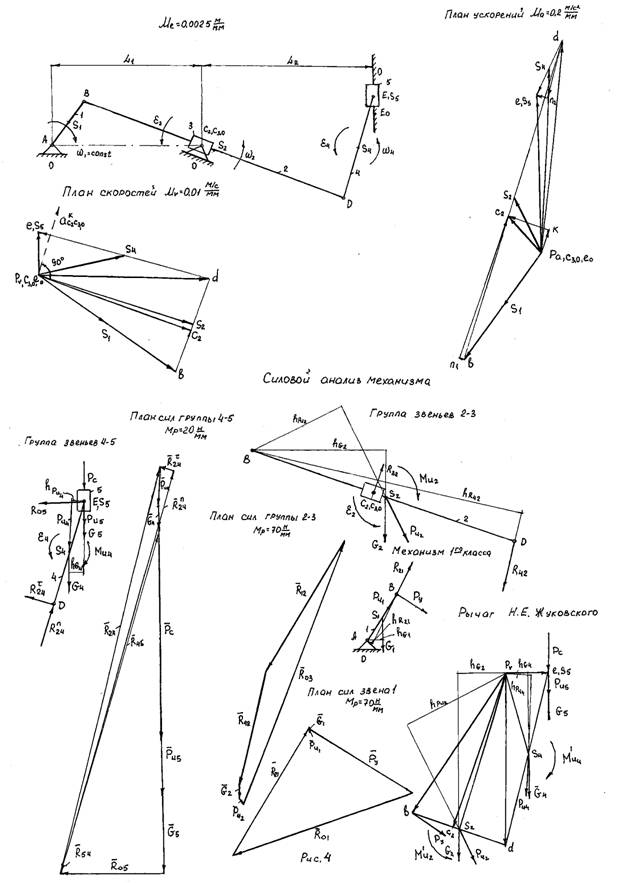
            1. Определяем силы инерции и моменты пар сил инерции звеньев
;

            ;
                        ;
                        ;
                        ;
                        .
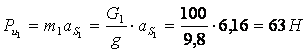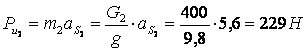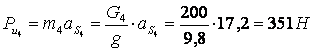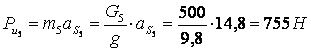Значения  и  см. стр.15.

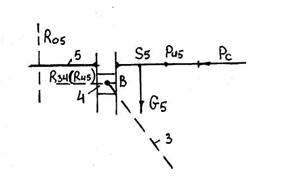
            2. Силовой анализ группы звеньев 4-5

                                       
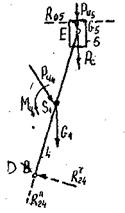
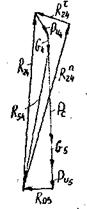
Рис.5

            Прикладываем все реальные силы, действующие на звенья группы (веса, силу сопротивления), силы инерции и моменты пар сил инерции ( и - направлены противоположно ускорениям центров масс, - противоположно ), силы реакции со стороны отброшенных частей механизма: реакция  - со стороны стойки на звено 5,  - реакция со стороны звена 2 на звено 4. Так как направление  неизвестно, раскладываем её на две составляющие:  - нормальную, направленную по звену и  - тангенциальную, направленную перпендикулярно к звену. Направление  и  выбираем произвольно.
Рассматриваем равновесие звена 4 и составляем уравнение моментов относительно точки Е
,
.
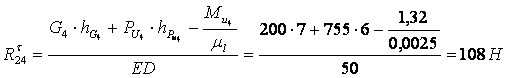Так как  получилась со знаком (+), то предварительно выбранное направление является истинным.
В уравнении  - масштаб схемы механизма вводится в том случае, если плечи сил берутся в миллиметрах непосредственно из чертежа, а момент пар сил инерции в ньютонометрах .
Рассматриваем равновесие группы в целом и составляем уравнение сил, действующих на группу.
.
В уравнении все силы инерции известны, кроме  и , которые известны лишь по направлению. Их можно определить, если решить это уравнение графически, то есть построить план сил. Выбираем масштаб плана сил  и проводи линию действия  параллельно звену 4. Из произвольной точки этой линии проводим вектор, из его конца  и т.д. в последовательности, в которой записаны силы в уравнении. Из конца вектора  проводим линию действия вектора  до пересечения с линией действия вектора . Точка их пересечения определяет величину каждой из них.
Направление должно быть таким, чтобы все векторы на плане следовали один за другим, то есть стрелки не должны встречаться. Суммируя графически  и , находим вектор . Величины определенных сил равны
;
.
Для определения реакций в шарнире Е () рассматриваем равновесие звена 4

Если построить план сил, то можно найти . Однако, следует отметить, что если уравнение равновесия группы составлять так, что сначала записывать силы, действующие на одно звено, а затем на другое, то дополнительного плана сил строить не надо, можно использовать уже построенный план для группы в целом. На этом плане необходимо конец вектора  соединить с началом вектора  и получим вектор  (см. рис.4,5).
Величина его равна
.

            3.Силовой анализ группы звеньев 2-3

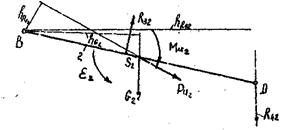
Рис.6
Рассматриваем равновесие звена 2 и составляем сумму моментов сил относительно точки В, при этом учитываем, что реакция  будет  звену BD. Направление её выбираем произвольно (рис.4,6)
;
.
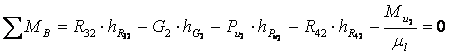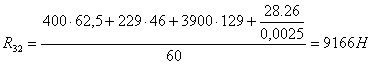Рассматриваем равновесие звена 3, на которое действуют только реакции со стороны звена 2 и стойки 0.


,          
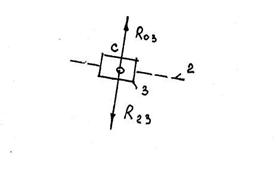
Для определения реакции  рассматриваем равновесие группы и составляем уравнение сил, действующих на неё
.

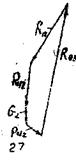
Рис.7
Принимаем масштаб  и строим план сил по этому уравнению (см. рис.4,7). Величина реакции  будет равна
.

            4. Силовой анализ механизма 1-го класса.
На механизм 1-го класса помимо реакции , веса , и силы инерции  будет действовать уравновешивающая сила , которую условно прикладываем в шарнире 5 перпендикулярно кривошипу AB (см. рис.4,8),

                                               
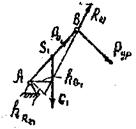
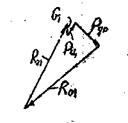
Рис.8
Для определения  составляем сумму моментов сил относительно точки А
;
.
Для определения реакции в шарнире А рассматриваем равновесие звена 1.
.
Принимаем масштаб  и строим план сил по этому уравнению (рис.4,8). Величина реакции будет равна
.

3. Определение уравновешивающей силы по методу Н.Е.Жуковского

            Для определения  по методу н.Е.Жуковского необходимо план скоростей повернуть на угол 900 и в соответствующих точках плана приложить все силы, действующие на механизм, включая силы инерции, моменты пар сил инерции и уравновешивающую сил. Затем составить уравнение моментов всех сил относительно полюса плана. В этом уравнении единственной неизвестной является уравновешивающая сила, которая и определяется из этого уравнения.
Следует знать, что моменты пар сил инерции, прикладываемые на плане скоростей относительно точек центров масс, могут либо оставаться по направлению такими же, как и на механизме, либо иметь противоположное направление. Если направление расположения букв на плане скоростей звена и на звене одинаков, то момент не изменяет направления (например, на рис.4 для звена BD и его плана  расположение букв b и d одинаково, то же и для звена ED). Если расположение букв на звене и на плане противоположно, то момент должен изменить знак на противоположный.
Если моменты пар сил инерции определены в ньютонометрах, а плечи сил на плане берутся в миллиметрах, то их надо пересчитать
;
,
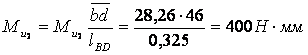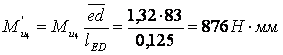где       и   - отрезки, взятые из повернутого плана скоростей, мм;
 и  - истинные размеры звеньев, м.
Составляем уравнение моментов относительно полюса плана скоростей и находим :

Определяем погрешность расчета  по планам сил и методу Н.Е.Жуковского
.

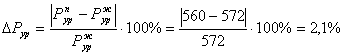4.Последовательность силового анализа групп 2-го класса

            1. Группа 1-го класса
Реакции в шарнирах B и D  раскладываем на нормальные и тангенциальные:

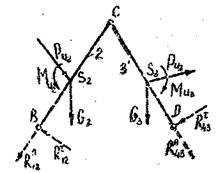
а) определяется реакция  из условия равновесия звена 2
;
б) определяется реакция  из условия равновесия звена 3
;
в) определяются реакции  , ,  и  из условия равновесия группы
.
Строится план сил по уравнению и определяются искомые реакции.
г) определяется реакция в шарнире С () из условия равновесия либо звена 2, либо3.
.

            2. Группа 2-го вида

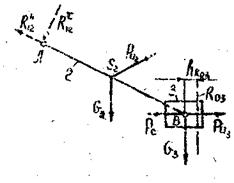
а) определяется реакция  из условия равновесия звена 2
;
б) определяются реакции ,  и  из условия равновесия группы
.
Строится план сил по уравнению и находятся искомые реакции (сила сопротивления  может отсутствовать, если звено 3 не является рабочим звеном).
в) определяется реакция в шарнире В () из условия равновесия либо звена 2, либо 3
;
г) определяется плечо реакции из условия равновесия звена 3
.

            3.Группа 3-го вида

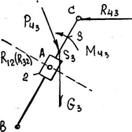
Поскольку в заданиях на курсовой проект отсутствует вес камня 2, то последовательность расчета проводится именно для этого частного случая:
а) рассматриваем равновесие звена 2
             ,
так как  к звену 3, то  тоже перпендикулярна звену 3.
б) определяется реакция  из условия равновесия группы
,
реакция  должна быть определена раньше из расчета группы, присоединенной к данной группе.
в) определяется реакция  (в шарнире В) из условия равновесия группы
.

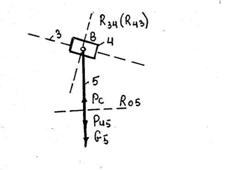
4. Группа 4-го вида

                                              
Весом камня 4 пренебрегаем. Реакция  к звену 3, а реакция  к направляющей. Сила сопротивления  может отсутствовать, если звено 5 не является рабочим.
а) определяются реакции  и  из условия равновесия группы

.
Строится план сил и находятся искомые реакции.
б) определяется реакция в шарнире В () из условия равновесия одного из звеньев, т.к. , то
;        ;
в) определяются плечи реакций  и  из условия равновесия звеньев 4 и5;
для звена 4     ;
для звена 5     .

            5. Группа 5-го вида

            Весом звена 4 пренебрегаем. Реакция  направляющей звена 4.
а) рассматриваем равновесие звена 4
;         ;
отсюда следует, что  к направляющей звена 4.
б) определяются реакции  и  из условия равновесия группы

Строится план сил и находятся искомые реакции ( - сила сопротивления может отсутствовать, если звено 5 не является рабочим)
в) определяется плечо реакции  из условия равновесия звена 5
.