КИНЕМАТИЧЕСКИЙ  АНАЛИЗ  МЕХАНИЗМА

            Кинематический анализ механизма проводится графоаналитическим методом, то есть с помощью планов скоростей и ускорений, строящихся для различных положений механизма.
Основными задачами кинематического анализа являются:
1.Построение планов положений механизма.
2.Построение планов скоростей и ускорений для различных положений механизма и определение по ним абсолютных скоростей и ускорений шарнирных точек и центров масс звеньев.
3.Определение величин и направлений угловых скоростей () и угловых ускорений () звеньев.

1. Построение планов положений механизма

            Планы положений механизма представляют собой совокупность кинематических схем механизма, построенных для различных положений входного звена.
При кинематическом исследовании принято строить положения для равностоящих друг от друга по времени положений входного звена, количество которых обычно принимается равным 12. Планы положений строят методом засечек в чертежном стандартном масшта­бе .
Построение планов положений начинается с построения крайних положений механизма, одно из которых (обычно соответствующее началу рабочего хода механизма) принимается за базовое (нулевое) положение. От нулевого положения начинается разбиение тра­ектории входногозвена на равноотстоящие положения и затем построение механизма для каждого положения входногозвена.
В основе всех механизмов, предусмотренных заданиями для данной курсовой работы, лежат три следующих типа механизма: кривошипно-ползунный, кривошипно-коромысловый и кривошипно-кулисный.
Рассмотрим определение крайних положений для всех трех выше перечисленных типов механизмов.
а) Крайнимиположениями для кривошипно-ползунного механизма являются положения, при которых шатун и кривошип лежат на одной прямой (см. рис.1). Для определения крайних положений ползуна В при заданных размерах шатуна и кривошипа и расстояния е (для аксиальных механизмов е=0) необходимо из центра враще­ния кривошипа О на прямой, по которой движется ползун, сделать две засечки радиусами

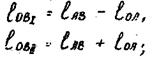
б) Для кривошипно-коромыслового механизма крайние положения определяется аналогично, как и для кривошипно-ползунного ме­ханизма. Разница заключается лишь в том, что траектория точки В  будет дугой окружности (рис.2).
в) Для кривошипно-кулисного механизма с качающейся кулисой крайние положения будут тогда, когда кривошип и кулиса образуют между собой прямой угол (рис.3), то есть крайние положения кулисы ВС будут касательными к траектории точки А. поэтому при заданных размерах кулисы, кривошипа и расстояния . Для построения крайних положений механизма проводится окружность из точки О радиусом, равным , из точки В проводятся касательные к окружности кривошипа, которые и являются крайними положениями кулисы ВС.
Обычно для кулисных механизмов задается коэффициент неравномерности скорости хода, представляющий собой отношение угла поворота кривошипа при рабочем ходе к углу поворота при холостом ходе:

Определив угол , можно рассчитать длину кривошипа

и затем построить крайние положения механизма.

2. Построение планов скоростей и ускорений

            План скоростей (ускорений) представляет собой графическое изображение абсолютных скоростей (ускорений) точек звеньев механизма, имеющее общее начало, называемое полюсом плана.
Метод планов скоростей (ускорений) основан на известных теоремах теоретической механики, согласно которым плоское движение твердого тела (звена) можно представить как сложное, состоящее из двух движений: переносного и относительного.
Метод планов скоростей и ускорений применим только для механизмов 2-го класса, т.е. механизмов, включающих в себя только двухподковые группы 2-го класса.
Для успешного решения задач, связанных с построением планов скоростей и ускорений, необходимо знать основные  свойства планов скоростей (ускорений):
1.Фигура, образованная планом относительных скоростей, подобна очертанию звена сходственно с ним расположена и повернута по отношению к звену на угол 900 в сторону мгновенного его вращения.
2.Фигура, образованная планом относительных ускорений, подобна очертанию звена, сходственно с ним расположена и повернута по отношению к звену на угол 1800 -  в сторону его мгновенного углового ускорения, где  - угол между полным и нормальным относительными ускорениями.
3.Векторы, исходящие из полюса плана, изображают абсолютные скорости (ускорения) точек звена.
4.Векторы, соединяющие концы векторов абсолютных скоростей (ускорений), изображают относительные скорости (ускорения) точек звеньев, причем, например, скорость точки В относительно А на плане изображается вектором, направленным на плане от точки а к точке b
5.План скоростей позволяет определить величину и направление угловой скорости по выражению  ,
где       - относительная скорость двух точек звена,
 - расстояние между точками.

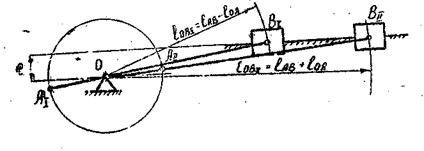
Рис. 1

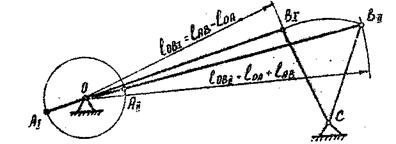
Рис. 2

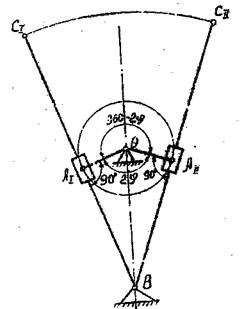
Рис. 3

            6.План ускорений позволяет определить величину и направление углового ускорения по выражению ,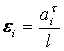
где       - тангенциальная составляющая полного относительного ускорения двх точек звена,  - расстояние между точками.
Кроме того, необходимо знать, что:
1.Относительная скорость при вращательном движении звена всегда направлена перпендикулярно к звену в сторону его угловой скорости.
2.Относительная скорость (ускорение) при поступательном движении одного звена относительно другого направлена всегда по направлению движения, т.е. параллельно направляющей
3.Нормальное ускорение всегда направлено по звену к центру вращения, например,  направлено по звену АВ от точки В к точке А, величина его равна .
4.Тангенциальное ускорение всегда перпендикулярно к нормальному и, следовательно, для звена, совершающего вращательное или плоскопараллельное движение перпендикулярно к звену, величина его равна . Для звена, совершающего поступательное движение относительно неподвижной направляющей  параллельно направляющей, .
5.Если звено совершает сложное движение, состоящее из переносного вращательного и относительного поступательного движений, то возникает кориолисово ускорение, величина которого определяется выражением
,
где       - относительная поступательная скорость,
 - угловая переносная скорость.
6.Направление кориолисова ускорения определяется поворотом вектора относительной скорости на 900 в сторону .

3. Последовательность построения планов скоростей (ускорений)

            Последовательность построения планов скоростей (ускорений) указывает формула строения механизма, получаемая в результате структурного анализа. Эта последовательность должна быть следующей:
1.Строится план скоростей (ускорений) механизма 1-го класса, после чего становится известной скорость (ускорение) концевого элемента кинематической пары группы, присоединенной к механизму 1-го класса.
2.Строится план скоростей (ускорений) 1-ой присоединенной группы: 1-ой присоединенной группой следует считать ту, которая одним поводком присоединяется к механизму 1-го класса, вторым к стойке; если таких групп несколько, то они равноценны и построение можно вести для любой из них. Для построения плана составляются уравнения для средней кинематической пары относительно концевых элементов, скорости (ускорения) которых известны, и решаются графически.
3.Строятся план скоростей (ускорений) для остальных групп механизма в порядке их присоединения, причем задача, как и в предыдущем пункте, сводится к определению скорости (ускорения) средней кинематической пары относительно известных концевых элементов.

4.Пример кинематического анализа

            Построить план скоростей и ускорений механизма, представленного на рис.4 в заданном положении, определить абсолютные скорости и ускорения шарнирных точек, ускорения центров масс звеньев, угловые скорости и ускорения звеньев.

Дано: , , , , , , центры масс звеньев находятся посредине.

Структурный анализ механизма

а) Наименование звеньев:
0-стойка, 1-кривошип, 2-шатун-камень, 3-коромысло-кулиса, 4-шатун, 5-ползун.
б) Классификация кинематических пар

           
в) Степень подвижности по формуле П.Л.Чебышева
;
г) Структурная схема механизма

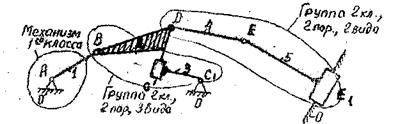
д) Формула строения механизма

Построение плана скоростей

Построение плана скоростей механизма 1-го класса

Определяем скорость точки В
.
Из произвольной точки  , принятой за полюс плана, проводим вектор , перпендикулярный звену АВ. Длина его может быть выбрана произвольной, однако для получения «удобного» масштаба плана принимаем его .
Определяем масштаб плана скоростей
.
Вектор  является планом скоростей механизма 1-го класса.

Построение плана скоростей первой присоединенной группы (звенья 2,3)

            Для этой группы известны скорости концевых элементов: точки В и точки С3 (С0). Необходимо определить скорость элемента средней пары – точки С2, которая в данный момент совпадает с точкой С3 (С0) (см. рис.4).
Составляем векторные уравнения для определения скорости точки  относительно точки В и
,
.
где       - абсолютная скорость точки ;
 - абсолютная скорость точки , известная по величине и направлению (подчеркнута двумя чертами);
 - относительная скорость точки  по отношению к , она , т.к. это скорость во вращательном движении точки  относительно  (известна по линии действия – подчеркнута одной чертой);
 - абсолютная скорость точки , совпадающая со скоростью точки ;
 - относительная скорость точки  относительно  в поступательном движении и следовательно направлена  звену .
Решаем эту векторную систему графически, для чего из точки В на плане проводим линию действия вектора  , а из точки , расположенной в полюсе, проводим линию вектора , точку пересечения их  соединяем с полюсом. Вектор  - есть вектор абсолютной скорости точки ,  - вектор относительной скорости точки , он же является планом скоростей части звена 2 от точки В до точки .
Скорость точки D, принадлежащей звену 2 и лежащей на его продолжении за точкой , находим, используя свойство подобия плана скоростей. Составляем пропорцию для нахождения положения точки d на плане
,
где      BD и  - линейные размеры, которые берутся прямо из схемы механизма, мм;
 - отрезок берется из плана скоростей, мм
Определив отрезок , откладываем его на плане, точка d будет лежать за точкой также, как и на звене. Вектор   - вектор абсолютной скорости точки D.

Построение плана скоростей 2-ой присоединенной группы (звенья 4-5)

            После определения скорости точки D для этой группы известны скорости концевых элементов: точки D и точки Е0, принадлежащей станине и совпадающей в данный момент с шарнирной точкой Е, которая является средней кинематической парой данной группы.
Составляем векторные уравнения для скорости точки Е относительно концевых элементов группы
,
.

где       - абсолютная скорость точки Е45;
 - абсолютная скорость точки D3,4 (на плане вектор );
 - относительная скорость точки  относительно ,  к
 - абсолютная скорость точки ;
 - относительная скорость точки  относительно   направляющей, по которой движется ползун 5.
Решаем данную систему графически. Из точки d на плане проводим линию вектора  к DE, а из точки е0, расположенной в полюсе, проводим линию вектора  направляющей, т.е. вертикально. Вектор  есть вектор абсолютной скорости точки Е.
4.Определяем скорости центров масс  и угловые скорости звеньев.
Так как центры масс лежат посредине звеньев, то на плане точки центров масс будут также лежать посредине соответствующих отрезков. Абсолютные скорости центров масс будут равны.
;
;
.
Совершенно аналогично определяются истинные значения абсолютных скоростей шарнирных точек механизма.
Угловые скорости звеньев будут равны
;
.
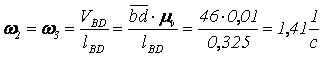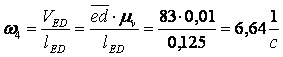Для определения направления угловой скорости  на план механизма переносим вектор относительной скорости  в точку D  (на плане скоростей этот вектор направлен от точки b к точке d) и смотрим, куда он вращает точку D относительно В. В данном случае против часовой стрелки.
Аналогично определяем направление .

Построение плана ускорений

            Определяем ускорение точки В, которое будет состоять только из нормальной составляющей, так как

                       
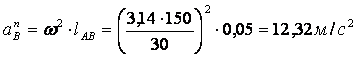
Из произвольной точки Ра, принятой за полюс плана, проводим вектор =61,6мм параллельно звену АВ и направленный от точки В к А.
Определяем масштаб плана ускорений

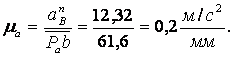
Вектор  является планом ускорений механизма 1-го класса.

Построение плана ускорений группы звеньев 2-3

            Составляем векторные уравнения для определения ускорения точки С2 относительно точек А и С3
;

где       - абсолютное ускорение точки С2;
 - нормальное ускорение точки С2 относительно В, оно направлено по звену 2 от точки С2 к точке В, величину его определяем, используя план скоростей

или в масштабе  отрезок на плане ускорений
,
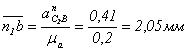где       - отрезок из плана скоростей;
 - тангенциальная составляющая ускорения точки С2 относительно В, линия действия его перпендикулярна  или к звену 2;
= 0 – абсолютное ускорение точки С3,0;
 - кориолисово ускорение точки С2 относительно С3, величина его равна

 – отрезок из плана скоростей, или в масштабе  отрезок на плане ускорений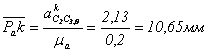
Направление его определяем согласно существующему правилу, поворачиваем вектор относительной скорости  относительно точки С3,0 в сторону  (в данном случае против часовой стрелки) на 900 (см. рис.4).
- относительное ускорение точки С2 относительно С3,0 направлено  звену 2.
Решаем систему векторных уравнений графически.
Из точки b на плане проводим вектор  и направленный от точки С2 к В, из точки  проводим линию действия тангенциального ускорения  к вектору . Переходим теперь к решению второго векторного уравнения системы, из точки С3,0, которая расположена в полюсе, проводим вектор , направление и величина которого определены выше. Из точки k проводим линию действия относительного ускорения, которая будет перпендикулярна к вектору . Точку пересечения линий тангенциального ускорения  и относительного  соединяем с полюсом. Вектор  - есть абсолютное ускорение точки С2.
Положение точки Dна плане находим из пропорции

3. Строим план ускорений группы звеньев 4-5
Составляем векторные уравнения для точки Е относительно точек Е0 и D
;
,
где       - абсолютное ускорение точки Е;
 - абсолютное ускорение точки D (вектор  на плане);
 - нормальное ускорение точки Е относительно D, направленное по звену ЕD от точки Е к точке D. Величина его равна
,
 - тангенциальное ускорение точки Е относительно D, направлено ;
= 0 – абсолютное ускорение точки Е0;
= 0 – кориолисово ускорение точки Е относительно Е0, равно нулю, потому что направляющая неподвижна;
 - относительное ускорение точки Е относительно Е0, направлено по движению ползуна 5.
Решаем векторные уравнения графически.
Из точки d проводим вектор нормального ускорения , длина которого равна . Из точки С0, находящейся в полюсе, проводим линию действия  по направлению движения ползуна Е. Точка пересечения  и  есть точка е, вектор  - абсолютное ускорение точки Е.
4.Определяем ускорения центров масс и угловые ускорения звеньев.
Соединяем середины отрезков ,  и  с полюсом, тогда векторы ,  и  будут абсолютными ускорениями центров масс звеньев, истинные значения ускорений получаем, умножив длины этих векторов на масштаб
;
;
;
.
Аналогично определяются истинные значения абсолютных ускорений шарнирных точек механизма.
Угловые ускорения звеньев будут равны
;
.
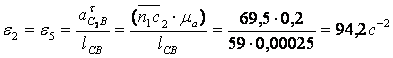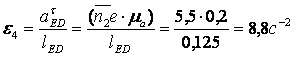Для определения направления углового ускорения на план механизма переносим вектор тангенциального ускорения  в точку С2 (на плане ускорений это , направленный от точки  к точке с2) и смотрим, куда он вращает точку С2 относительно В. В данном случае против часовой стрелки.
Аналогично определяется направление .