СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

            Методы кинематического и силового анализа механизмов находятся в прямой зависимости от типа структурных групп, образующих механизм. Поэтому для выяснения методов кинематического и силово­го исследования механизмов и их последовательности необходимо предварительно провести структурный анализ механизма, который позволил бы установись класс механизма и последовательность присоединения структурных групп при его образовании.

1. Основные понятия и определения

            Звено – одна или несколько деталей, не имеющих относительной подвижности.
Кинематическая пара – соединение двух соприкасающихся звеньев, обеспечивающее их относительную подвижность.
Существуют две классификации кинематических пар: по Артоболевскому и Рело.
Класс кинематической пары по Артоболевскому определяется количеством условий связи, накладываемых парой на относительную подвижность звеньев.
По Рело кинематические пары делятся на высшие и низшие.
Высшая кинематическая пара – это пара, в которой требуемое относительное движение звеньев может быть получено только соприкосновением её элементов по линии или в точке.
Низшая кинематическая пара – это пара, в которой требуемое относительное движение звеньев может быть получено только соприкосновением её элементов по поверхности.

Как правило, пары высшие являются парами 4-го класса по классификации Артоболевского, пары низшие – пары 5-го класса.

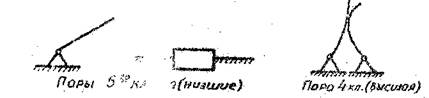
Кинематическая цепь – связанная система звеньев, образующих кинематические пары.
Механизм – кинематическая цепь, обладающая свойством определенности движения, то есть цепь, у которой при заданных законах движения входных звеньев остальные совершают вполне определенное движение. У механизма количество входных звеньев должно быть равно степени подвижности W, определяемой по формуле П.Л.Чебышева.
Всякий механизм состоит из одного или нескольких механизмов 1-го класса и присоединенных структурных групп.
Механизм 1-го класса – входное звено со стойкой. Существует два механизма 1-го класса: с вращательной и поступательной парой.
                                    

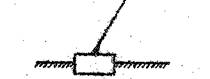
Механизм 1-го класса                                               Механизм 1-го класса
с вращательной парой                                            с поступательной парой

            Структурная группа – кинематическая цепь, которая при соединении её свободными элементами кинематических пар к стойке имеет степень подвижности равную 0 () и которая не может быть расчленена на более простые кинематические цепи с нулевой степенью подвижности.
Структурные группы подразделяются на классы.
Класс группы определяется наивысшим классом контура, образуемого внутренними кинематическими парами группы.
Внутри класса группы подразделяются на порядки.
Порядок группы определяется количеством свободных элементов кинематических пар, которыми группа может быть присоединена к стойке или образованной уже цепи механизма.
                                               
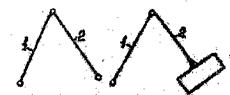
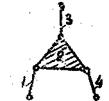
Группа 2-го класса 2-го порядка                                       Группа 3-го класса 3-го порядка

Класс механизма определяется наивысшим классом группы, входящей в механизм.
Структурная схема – это схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение.
Структурная схема строится без масштаба.

2. Условия перехода от кинематической схемы к структурной

            При изображении структурной схемы на основании кинематической схемы механизма необходимо выполнять следующие требования:
1.Пассивные звенья, имеющиеся в механизме, должны быть отброшены и не учитываться при подсчете степени подвижности по формуле Чебышева, так и при изображении структурной схемы.
2.Сложные шарниры необходимо расчленить на простые, при этом надо учитывать, что в сложном шарнире содержится простых шарниров на единицу меньше пересекающихся в нём звеньев. За базовое звено необходимо принимать звено, образующее кинематическую пару со стойкой.
3.Высшие пары необходимо заменить низшими. Одна высшая пара заменяется звеном с двумя низшими парами.
4.Звенья, входящие в более, чем в две кинематические пары, должны изображаться соответствующими контурами (например, звено, входящее в три пары, на схеме изображается треугольником и т.п.).
5.Допускается замена поступательных пар на вращательные.
6.Нумерация звеньев на кинематической и структурной схемах должна быть одинаковой. При этом звенья, появляющиеся в результате замен высших пар низшими, нумеруются с дополнительной индексацией (например, ,  и т.п.)
3. Последовательность структурного анализа

            1.Дается наименование звеньев механизма.
2. Выделяются кинематические пары и устанавливается их класс по классификации Артоболевского и Рело.
3.Определяется степень подвижности по формуле П.Л.Чебышева и устанавливается, является ли исследуемая кинематическая цепь действительно механизмом.
4.Вычерчивается структурная схема механизма.
5.Выделяются структурные группы и устанавливается их класс и порядок (для групп 2-го класса определяется также и вид ).
6.Устанавливается класс всего механизма и записывается формула его строения.

4. Пример структурного анализа механизма

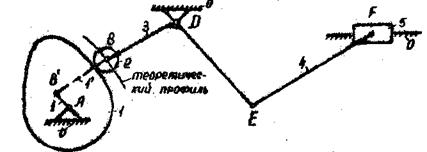
1. Наименование звеньев:
1–кулачок, 2-ролик (пассивное звено), 3-толкатель, 4-шатун, 5-ползун, 0-стойка
2. Классификация кинематических пар
Освобождаемся от пассивного звена 2, тогда толкатель 3 будет контактировать по теоретическому профилю (на схеме контактирующий конец изображен стрелкой).

3. Степень подвижности по формуле П.Л.Чебышева

 - число подвижных звеньев (звено 2 не учитывается),
 - пары 5-го класса,
 - пары 4-го класса.
Следовательно, исследуемая кинематическая цепь является механизмом при одном ведущем звене.
4. Структурная схема механизма
Заменяем высшую пару низшими (см. кинематическую схему), появляющееся в результате замены дополнительное звено обозначаем , звено3 на схеме должно быть изображено треугольником.

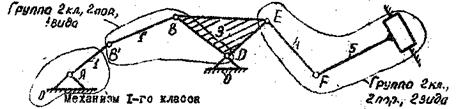
            Следовательно, исследуемый механизм является механизмом 2-го класса.
5. Формула строения механизма
.