|
Кулачковый механизм
с роликовым толкателем
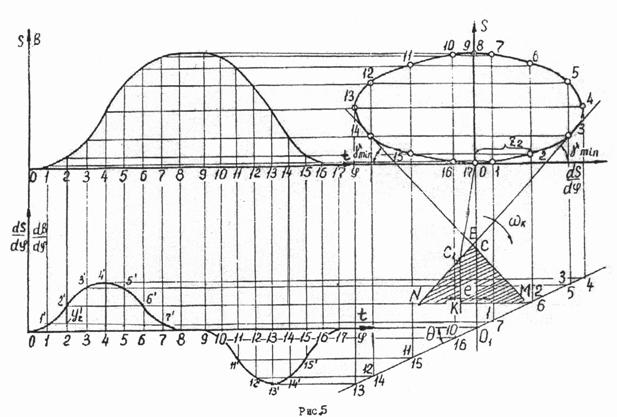
Для определения минимального радиуса кулачка, представленного на рис.1 а, необходимо построить совмещенную диаграмму перемещений 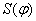 и аналога скорости и аналога скорости 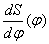 . Совмещенная диаграмма строится в масштабе . Совмещенная диаграмма строится в масштабе 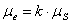 (k=1,2,3,… и т.д.), одинаковом для обеих осей диаграммы. Если принимается масштаб (k=1,2,3,… и т.д.), одинаковом для обеих осей диаграммы. Если принимается масштаб 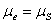 , то ординаты по оси S получаются путем прямого переноса их с диаграммы , то ординаты по оси S получаются путем прямого переноса их с диаграммы 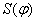 (рис.5), а абсциссы диаграммы определяются по формуле: (рис.5), а абсциссы диаграммы определяются по формуле:
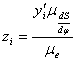 , ,
где 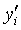 - текущее значение ординаты, взятое из диаграммы - текущее значение ординаты, взятое из диаграммы 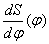
Например:
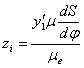 , , 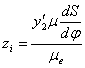 . .
При этом абсциссы Zi для угла удаления при вращении кулачка по часовой стрелке откладываются вправо от оси S, при вращении против часовой стрелки - влево.
Если масштаб 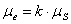 , то по оси S совмещенной диаграммы необходимо откладывать ординаты из диаграммы перемещений , то по оси S совмещенной диаграммы необходимо откладывать ординаты из диаграммы перемещений 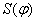 , уменьшенные в kраз. , уменьшенные в kраз.
Построение диаграммы можно осуществить графическим путем, для чего необходимо определить значение угла 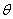 по формуле: по формуле:
<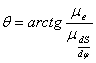 , ,
и провести прямую под углом 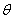 к оси j диаграммы к оси j диаграммы 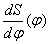 в точке ее пересечения с продолжением оси S совмещенной диаграммы (точка O1 на рис.5) и снести ординаты диаграммы в точке ее пересечения с продолжением оси S совмещенной диаграммы (точка O1 на рис.5) и снести ординаты диаграммы 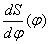 как показано на рис. 5. как показано на рис. 5.
К построенной совмещенной диаграмме проводятся две касательные под углом 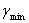 , которые, пересекаясь, выделяют область, в которой может располагаться центр вращения кулачка (заштрихованная область). Если по заданию эксцентриситет равен ε = 0, то расстояние OC в масштабе , которые, пересекаясь, выделяют область, в которой может располагаться центр вращения кулачка (заштрихованная область). Если по заданию эксцентриситет равен ε = 0, то расстояние OC в масштабе 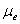 является минимальным радиусом кулачка, то есть является минимальным радиусом кулачка, то есть 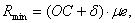 где где 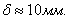
Если задан эксцентриситет e, то на расстоянии 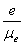 от прямой OO1, до пересечения в точке C1 со стороной EN угла NEM. Отрезок OC1 является минимальным радиусом кулачка при заданном эксцентриситете в масштабе от прямой OO1, до пересечения в точке C1 со стороной EN угла NEM. Отрезок OC1 является минимальным радиусом кулачка при заданном эксцентриситете в масштабе 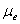 . Истинная величина радиуса будет равна . Истинная величина радиуса будет равна
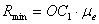 . .
|
