4. Силовой анализ механизма.[5.стр.209-211]

Силовой анализ механизма позволяет найти усилия, действующие на звенья механизма (необходимы для расчета звеньев механизма на прочность) и уравновешивающее усилие (необходимо для подбора мощности приводного двигателя). Этот анализ для заданного положения механизма проводится мето¬дом планов сил в порядке, обратном формуле строения механизма. Сначала рассчитывается структурная группа 2-3, а затем механизм I-го класса.

Излагаемая ниже методика силового анализа иллюстрируется примерами расчета для КПМ по данным табл.1.

4.1 Определение внешних усилий на звенья механизма.
Для КПМ по данным табл. I находим:

4.1.1. Веса звеньев (силы тяжести).

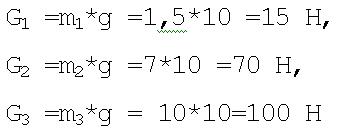
где g= 10м/с2 - ускорение силы тяжести.
. 4.1.2. Силы инерции звеньев

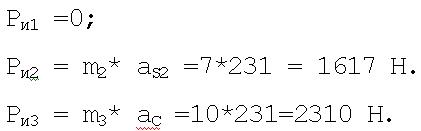
4.1.3. Моменты пар сил инерции

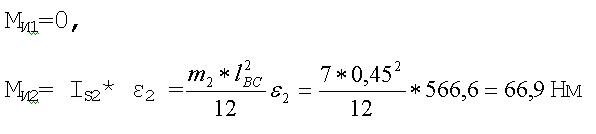
4.1.4. Усилие полезного сопротивления

РС=900 Н (задается в табл. I).

1.2. Силовой анализ структурной группы

Задачей этого анализа является определение реакций в кинематических парах группы.

4.2.1. Силовой анализ структурной группы 2-3 КПМ.
В масштабе вычерчиваем группу (рис.3a) в том положении, для которого проводился кинематический анализ, для стандартного масштаба

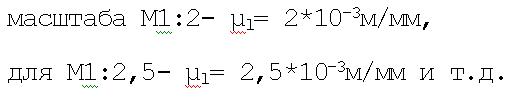
Прикладываем усилия, действующие на звенья группы. Силы тяжести приложены в центрах масс S2 и C , направлены вертикально вниз. Здесь же приложены силы _инерции РИ2 и РИ3. Векторы этих сил параллельны векторам Pas2и Pac(абсолютные ускорения центров масс), но направлены в противоположную сторону. В точке С параллельно направляющей приложена сила полезного сопротивления РС, направленная противоположно вектору Pvc. В кинематических парах В и С приложены реакции отброшенных звеньев. Эти реакции неизвестны, поэтому в кинематической паре В представим их в виде составляющих, одна из которых направлена вдоль эвена BC (нормальная составляющая Rⁿ₁₂) и вторая - перпендикулярна звену BC (тангенциальная составляющая R^t₁₂).

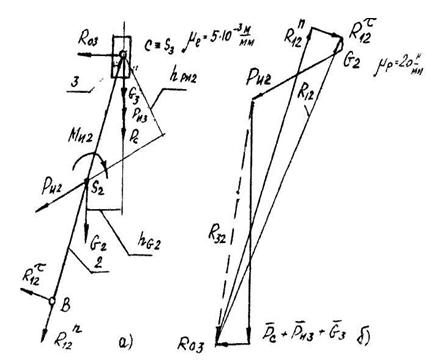
Рис.3 Структурная группа КПМ с приложенными усилиями(а) и план сил группы (б).

Направление векторов этих составляющих выбирается произвольно. Поскольку звено 3 совершает поступательное движение вдоль неподвижной направляющей, реакция RО3 в паре С (3,0) направлена перпендикулярно направляющей, то есть известна линия её действия (рис.3а)

Кроме инерционных сил РИ2 и РИ3 на звено действует момент пар сил инерции МИ2, направление которого противоположно направлению углового ускорения e2.

Согласно принципу Даламбера[5.стр.186] структурная группа под действием приложенных нагрузок находится в равновесии. Запишем условие равновесия группы в геометрической (векторной) форме.

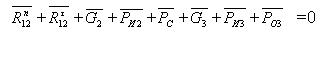
Составим уравнение моментов относительно точки С для звена 2, уравнение равновесия имеет вид:

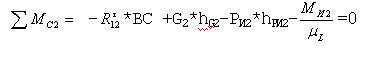
откуда находим

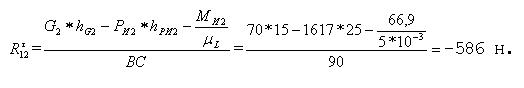
где ВС - длина звена 2, измеренная в мм на чертеже группы;
hРИ2- плечо силы РИ2 относительно точки С, это перпендикуляр, опущенный из точки С на линию действия силы РИ2 (измеряется на чертеже в мм);

hG2 - плечо силы G2 в мм.
Так как R^x₁₂<0,это усилие направляется противоположно принятому на рис.3а.

Определив величину и направление силы R^x₁₂, решаем графически уравнение равновесия группы, то есть строим план сил. Выбираем масштаб плана сил P. Он обычно выбирается по наибольшей силе таким образом, чтобы вектор силы на чертеже был 100*200 мм.
В нашем случае из действующих сил наибольшая сила РИ3 =2310 Н, выбираем отрезок II5,5 мм, тогда

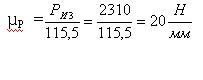
Вычисляем длины векторов, которыми будут изображаться силы на плане сил в масштабе.

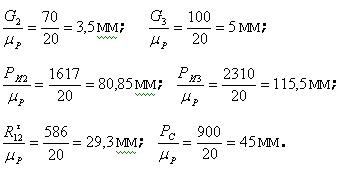
План сил строим в такой последовательности:

- проводим линию действия силы R^x₁₂, то есть прямую параллельную ВС;

- в произвольной точке прямой откладываем вектор силы R^x₁₂(в нашем случае отрезок 29мм) перпендикулярно прямой; его направление противоположно принятому на чертеже(рис.За).

- из конца вектора R^x₁₂откладываем вектор G₂(в нашем случае 3,5 мм) и т.д. в соответствии с векторным уравнением равновесия, то есть складываем векторы геометрически;

-наконец, из конца вектора P_из проводим линию действия вектора P_оз(прямую, перпендикулярную направляющей) до пересечения с линией действия вектора R^x₁₂; точка пересечения дает решение векторного уравнения равновесия группы.

Расставляем стрелки векторов таким образом, чтобы векторы следовали один за другим, так как их сумма равна нулю. Суммируя графически R^x₁₂и R^x₁₂, находим величину реакции R12.. Из плана сил имеем, (измерив соответствующие векторы в мм):

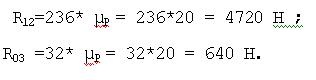
Используем план сил (рис.3б) и соединим конец вектора Pи2 с началом вектора R^x₁₂ . Получаем вектор R32(штриховая линия). Этот вектор есть графическое решение векторного уравнения равновесия звена 2. Определим величину R32, измерив величину вектора в мм.
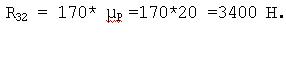