|
1.1 Нагрузки и напряжения. тензор напряжений
Рассмотрим произвольное тело с наложенными на него опорными связями, которое находится под действием поверхностных и объемных (массовых) нагрузок (рис. 1.1). Объемными нагрузками могут быть, например, собственный вес, инерционные силы, силы электромагнитного происхождения и т. д.
Поверхностные и массовые нагрузки характеризуются интенсивностями, которые в общем случае зависят от координат х, у, z и выражаются соответственно в Н/м2 (или Па) и Н/м3. Сосредоточенные внешние силы, приложенные в точках поверхности тела, можно рассматривать как предельный случай поверхностных нагрузок, распределенных на малой части поверхности тела.
Проекции интенсивности поверхностной нагрузки на координатные оси обозначим рх, ру, pz, а проекции интенсивности массовой нагрузки — X, Y, Z. Проекция интенсивности внешней нагрузки считается положительной, если ее направление совпадает с направлением соответствующей координатной оси. Под действием заданных нагрузок в теле появляются напряжения. Вырежем из рассматриваемого тела элементарный параллелепипед, ребра которого параллельны координатным осям, а их длина равна dх, dу, dz (см. рис. 1.1).
Вырежем из рассматриваемого тела элементарный параллелепипед, ребра которого параллельны координатным осям, а их длина равна dх, dу, dz (см. рис. 1.1). На гранях этого параллелепипеда действуют напряжения, которые можно разложить на нормальную составляющую к грани (нормальное напряжение) и касательную (касательное напряжение). В свою очередь, касательное напряжение можно разложить на две составляющие, параллельные координатным осям (рис. 1.2). В результате на каждой грани параллелепипеда действуют три напряжения (слово «составляющая» в дальнейшем для краткости будем опускать), которые обозначим σхх, τху, τхz. Первый индекс в обозначениях напряжений указывает ось, параллельно которой направлена внешняя нормаль к площадке, а второй индекс — ось, параллельно которой направлена составляющая напряжения, т. е. первый индекс указывает площадку, на которой действует напряжение, а второй — его направление. Поскольку в обозначениях нормальных напряжений фигурируют два одинаковых индекса, обычно оставляют только один из них и пишут σх,σy, σz.
Примем следующее правило знаков для напряжений: если внешняя нормаль к площадке имеет положительное (отрицательное) направление, то напряжение положительно, если его направление совпадает с положительным (отрицательным) направлением соответствующей координатной оси. В соответствии с приведенным правилом знаков положительные нормальные напряжения являются растягивающими, а отрицательные – сжимающими.
Напряжения, так же, как и поверхностная нагрузка, выражаются в Н/м2 (Па).
Одноименные и параллельные напряжения, действующие на параллельных гранях бесконечно малого параллелепипеда, отличаются друг от друга на бесконечно малую величину и потому их можно считать одинаковыми.
Следовательно, на гранях параллелепипеда действуют три нормальных и шесть касательных напряжений, совокупность которых образуют тензор напряжений
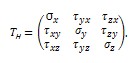
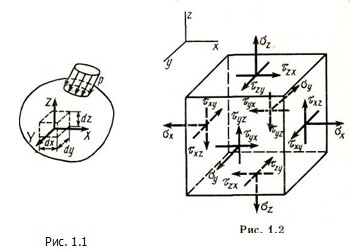
В строках тензора содержатся напряжения, направление которых параллельно соответственно координатным осям x, y, z, а в столбцах – напряжения, действующие на площадке, нормаль к которой параллельна оси х, или у, или z.
Для общего случая напряженного состояния доказан закон парности касательных напряжений. В соответствии с ним τxy=τyx, τyz=τzy, τzx=τxz
Следовательно, тензор напряжений является симметричным относительно главной диагонали.
Наряду с напряжениями, действующими на площадках, нормальных к координатным осям х, у, z, часто возникает необходимость отыскания напряжений на площадках, произвольным образом на¬клоненных к указанным осям. Установим зависимость между проекциями полного напряжения на наклонной площадке Xν, Yν, Zν с напряжениями σx,τxy,...
Выделим в окрестности точки элементарный тетраэдр, три грани которого совпадают с координатными плоскостями, а четвертая грань образована секущей произвольной наклонной плоскостью (рис. 1.3, а, б). Ее положение в пространстве определяется нормалью v . Обозначим косинусы углов (направляющие косинусы), образованные этой нормалью с осями x, y,z, cos(x,ν)=l, cos(y,ν)=m, cos(z,ν)=n.
Площадь наклонной грани равна dA, а площади других граней соответственно равны dAx, dAy, dAz (индекс указывает направление нормали к площадке).
Очевидно, что для этих площадей справедливы соотношения
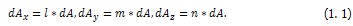
Условие равновесия тетраэдра в проекции на ось x имеет вид
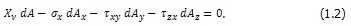
При записи уравнения равновесия удерживались только члены второго порядка малости (  , ...). , ...).
Поэтому горизонтальная проекция массовой силы не учитывается, так как она является величиной третьего порядка малости.
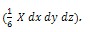
Из равенства (1.2) имеем
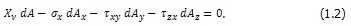
Далее из уравнений равновесия в проекции на оси у и z нетрудно получить аналогичные выражения для Yν, Zν . Однако те же самые равенства можно записать, воспользовавшись так называемым правилом круговой подстановки индексов. В итоге приходим к системе уравнений
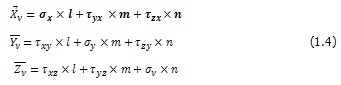
Таким образом, по известным компонентам тензора напряжений, записанным в осях х, у, z, могут быть найдены проекции полного напряжения Xν, Yν, Zν на наклонной площадке, определяемой направляющими косинусами l, m, n.
Обозначим координатную ось, совпадающую с нормалью через
х и выберем на наклонной площадке две другие ортогональные
оси у', z'.
По составляющим 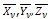 , можно получить значение нормального напряжения на той же площадке: , можно получить значение нормального напряжения на той же площадке:
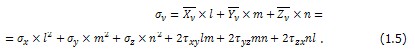
Далее ->
|



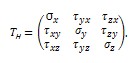

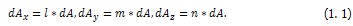
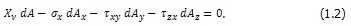
 , ...).
, ...). 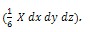
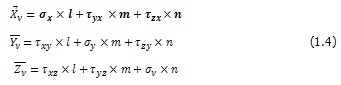
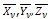 , можно получить значение нормального напряжения на той же площадке:
, можно получить значение нормального напряжения на той же площадке: