|
6.1. УРАВНЕНИЕ БАЛАНСА РАСХОДА СМАЗКИ
При решении задачи распределения давления в смазочном слое необходимо выполнить граничные условия для давления на кромке питателя, имеющие вид 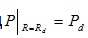 в реальном потоке, следовательно, в фиктивном потоке функция U(ξ) должна удовлетворять условию в реальном потоке, следовательно, в фиктивном потоке функция U(ξ) должна удовлетворять условию 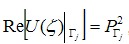 , где j =1, 2,….m. Однако, PГ, или в нашем случае Pd , неизвестно. Задавая давление подачи газа в подшипник Ps, в зависимости от вида питателя получаем различные значения Pd на кромке питателя. Для определения Pd необходимо дополнительное уравнение. Таким уравнением является уравнение баланса расходов смазки втекающей через питатель и протекающей через боковую поверхность цилиндра высотой h и радиуса d+0 , где j =1, 2,….m. Однако, PГ, или в нашем случае Pd , неизвестно. Задавая давление подачи газа в подшипник Ps, в зависимости от вида питателя получаем различные значения Pd на кромке питателя. Для определения Pd необходимо дополнительное уравнение. Таким уравнением является уравнение баланса расходов смазки втекающей через питатель и протекающей через боковую поверхность цилиндра высотой h и радиуса d+0
M=Q (6.12)
где М – расход смазки через питатель определяется формулой (4.1), а расход смазки через боковую поверхность цилиндра Q формулой (5.7).
Вычисляя среднеквадратичное значение давления на кромке питателя формуле
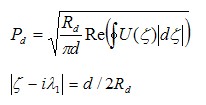
с использованием теоремы о среднем для гармонической в круге функции получим
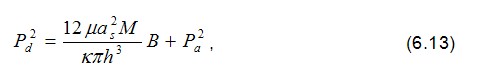
где

В случаях, когда n λ ≥ 3, для вычисления B можно применить приближённую формулу

Из соотношения (6.12) следует, что
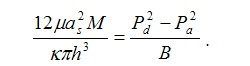
Пользуясь формулой (4.2),получаем уравнение для отыскания давления на кромке питателя

где 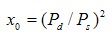 - квадрат безразмерного давления на кромке питателя, - квадрат безразмерного давления на кромке питателя,
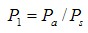 - безразмерного давления на кромках подшипника, - безразмерного давления на кромках подшипника,
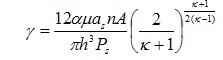 -конструктивный параметр наддува. -конструктивный параметр наддува.
При этом,
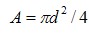 - для питателя типа ”простая диафрагма”,с диаметром минимального сечения d; - для питателя типа ”простая диафрагма”,с диаметром минимального сечения d;
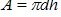 для питателя типа ”кольцевая диафрагма”. для питателя типа ”кольцевая диафрагма”.
|


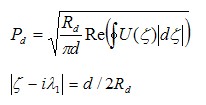
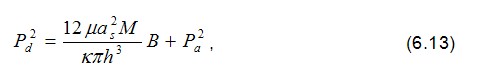


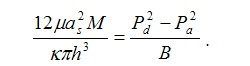


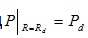 в реальном потоке, следовательно, в фиктивном потоке функция U(ξ) должна удовлетворять условию
в реальном потоке, следовательно, в фиктивном потоке функция U(ξ) должна удовлетворять условию 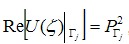 , где j =1, 2,….m. Однако, PГ, или в нашем случае Pd , неизвестно. Задавая давление подачи газа в подшипник Ps, в зависимости от вида питателя получаем различные значения Pd на кромке питателя. Для определения Pd необходимо дополнительное уравнение. Таким уравнением является уравнение баланса расходов смазки втекающей через питатель и протекающей через боковую поверхность цилиндра высотой h и радиуса d+0
, где j =1, 2,….m. Однако, PГ, или в нашем случае Pd , неизвестно. Задавая давление подачи газа в подшипник Ps, в зависимости от вида питателя получаем различные значения Pd на кромке питателя. Для определения Pd необходимо дополнительное уравнение. Таким уравнением является уравнение баланса расходов смазки втекающей через питатель и протекающей через боковую поверхность цилиндра высотой h и радиуса d+0
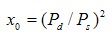 - квадрат безразмерного давления на кромке питателя,
- квадрат безразмерного давления на кромке питателя,
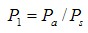 - безразмерного давления на кромках подшипника,
- безразмерного давления на кромках подшипника,
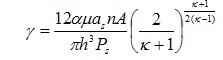 -конструктивный параметр наддува.
-конструктивный параметр наддува.
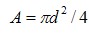 - для питателя типа ”простая диафрагма”,с диаметром минимального сечения d;
- для питателя типа ”простая диафрагма”,с диаметром минимального сечения d;
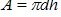 для питателя типа ”кольцевая диафрагма”.
для питателя типа ”кольцевая диафрагма”.