Полученную систему уравнений (2.8) (2.9) ,содержащую лишь давление и силы вязкого трения, можно преобразовать и свести к одному уравнению отно-сительно функции давления. Проделаем преобразования для случая упорного подшипника. Пусть одна из смазываемых поверхностей неподвижна, а другая, вращаясь с угловой скоростью ω , прецессирует с угловой скоростью Ω относительно оси подшипника. Для описания движения смазки введём углы Эйлера:
Ввиду малости величины зазора, tgθ <<1. Величина зазора подшипника меняется по закону h=h( φ , R, t)

Исходя из кинематических уравнений Эйлера и условия прилипания частиц газа на смазываемых поверхностях, граничные условия для скорости имеют вид:
на подвижной поверхности при z=h

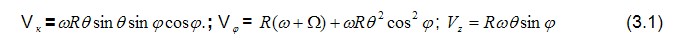на неподвижной поверхности при z=0

Условия прилипания на подвижной поверхности можно упростить, оставляя лишь слагаемые первого порядка малости и отбрасывая малые второго порядка 0( θ²), тогда

Полученные значения скоростей позволяют усреднить по толщине слоя уравнения неразрывности, используя при этом формулу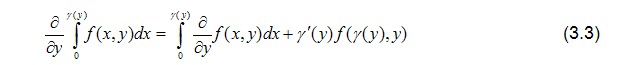

или интегрируя по z, получим

Интегрируя первое уравнение системы (2.8) , используя граничные условия радиальной составляющей скорости на поверхностях подшипника V_P=0 при z=0 и z =h , с учётом постоянства давления по толщине слоя ∂ P'/∂ z, устанавливаем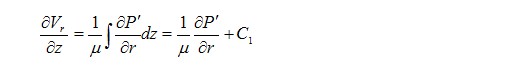

после интегрирования приходим к значению радиальной составляющей скорости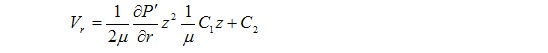

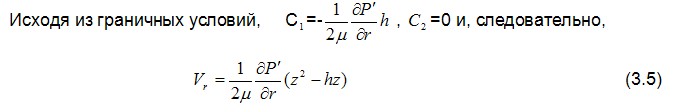Дифференциальное уравнение (3.8) описывает распределение давления газа в зазоре упорного подшипника и называется уравнением Рейнольдса.