

|
2. УРАВНЕНИЯ ГАЗОВОЙ СМАЗКИ В общем случае состояние и течение газовой смазки в зазоре подшипника можно описать, исходя из уравнений движения вязкой жидкости (уравнений Навье – Стокса) 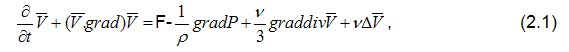 уравнения неразрывности  уравнения энергии 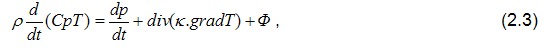
где Ф - диссипативная функция;,

где R – газовая постоянная, Т – температура по Кельвину.
 где Т0 , μ0 - соответствуют некоторому первоначальному состоянию газа. К полученной системе уравнений необходимо присоединить уравнение движения подвижного элемента. Решение полученной системы существенно нелинейных дифференциальных уравнений, даже численно, представляет сложную математическую задачу. Однако рассматриваемую задачу можно значительно упростить, если ввести ряд допущений классической теории газовой смазки:
1) Смазочное вещество может рассматриваться как сплошная среда. Такое допущение позволяет отвлечься от того факта, что любая среда состоит из дискретных частиц и рассматривать газовую смазку как некоторую сплошную среду;
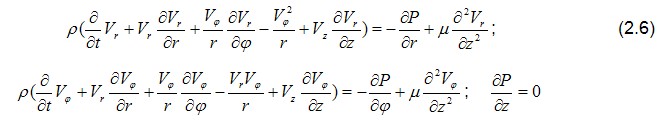 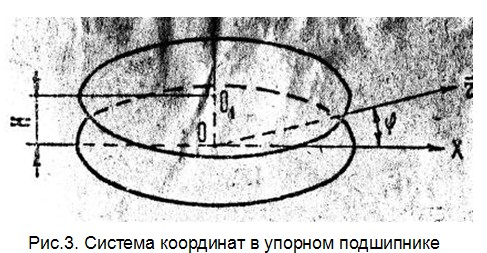
Слагаемые, входящие в левые части уравнений системы (2.6), отображают силы инерции, действующие на газовый слой в зазоре подшипника. При скоростях вращения до 30 – 40 тыс. об/мин. силами инерции можно пренебречь по отношению к вязким силам, определяемым слагаемыми 
где V-скорость частицы газа; R-характерный размер (радиус подшипника);
В большинстве случаев соотношение (2.7) справедливо, однако, с ростом относительной скорости движения смазываемых поверхностей Х растёт. При значительных скоростях пренебрежение силами инерции приводит к погрешности в 10 и более процентов.
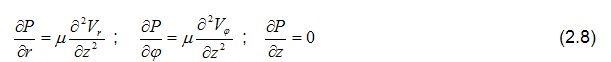 Для того чтобы система уравнений, определяющая поведение газового слоя, бала замкнута, необходимо добавить к системе уравнений (2.8) уравнение неразрывности 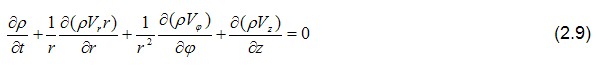
|

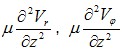 при этом необходимо, чтобы отношение этих сил было много меньше единицы
при этом необходимо, чтобы отношение этих сил было много меньше единицы