|
12. ОСНОВНЫЕ ПОЛОЖЕНИЯ СИСТЕМЫ FLEX.PDE
Flex.PDE – программа, предназначенная для построения сценарных моделей решения дифференциальных уравнений методом конечных элементов. Т.е. по сценарию, написанному пользователем, FlexPDE производит операции, необходимые для того, чтобы преобразовать описание системы дифференциальных уравнений в частных производных в модель для расчета методом конечных элементов, найти решение для этой системы и представить результаты в графической форме.
Flex.PDE выполняет роль вычислительной среды для решения задач, поскольку в этой программе заключен полный набор функций, необходимых для решения системы дифференциальных уравнений в частных производных.
Flex.PDE позволяет решать системы дифференциальных уравнения первого или второго порядка в частных производных. Система дифференциальных уравнений может быть стационарной или зависимой от времени. В рамках одной задачи могут быть рассмотрены стационарные и нестационарные уравнения одновременно. Число уравнений в системе, определяется мощностью компьютера, на котором установлен математический пакет FlexPDE. Уравнения могут быть линейными или нелинейными. Математический пакет FlexPDЕ решает нелинейные системы методом Ньютона - Рафсона.
Может быть задано любое количество геометрических областей для решения с различными свойствами материала. Предполагается, что переменные, описывающие модель, непрерывны на границах раздела сред.
FLEXPDE - ОСНОВЫ ПРОГРАММИРОВАНИЯ В СРЕДЕ
Сценарий описания задачи представляет собой текстовый файл. Содержание этого файла представляет собой ряд разделов, каждый из которых идентифицируется при помощи заголовка. Чаще всего используются следующие разделы:
TITLE - заголовок программы;
SELECT –раздел задания параметров задачи;
INITIALVALUES – раздел задания начальных значений для нелинейных задач;
VARIABLES – раздел задания переменных задачи;
DEFINITIONS – раздел задания вспомогательных переменных задачи;
EQUATIONS – раздел задания уравнений;
BOUNDARIES – раздел задания граничных условий;
PLOTS – раздел вывода графических результатов;
END – обозначает конец программы.
FlexPDE - Граничные условия
В сценарии FlexPDE, граничные условия описываются последовательно, по мере описания границы раздела сред.
Существует два основных типа задания граничных условий - VALUE и NATURAL
В граничные условия в форме VALUE (или по Дирихле) определяется значение, которое должна принять переменная на границе области решения.
В граничных условиях в форме NATURAL задается значение потока на границе области решений
К примеру, для представленной диффузионной задачи мы можем добавить фиксированные значения определяемой величины на верхнем и нижнем крае области и приравнять к нулю производную на боковых сторонах, как описано ниже:
BOUNDARIES
region1
start(0,0)
value(u) = 0 line to (1,0) { значение на нижней границе }
natural(u)=0 line to (1,1) { значение на правой границе }
value(u)=1 line to (0,1) { значение на верхней границе }
natural(u)=0 line to finish { значение на левой границе }
Flex.PDE - Постановка задачи
Самый простой путь к постановке задачи состоит в копировании решения для аналогичных задач, которые уже имеются у пользователя. В любом случае, следует определить четыре основных составляющих сценария:
- Определить переменные и уравнения
- Определить область решений и граничные условия
- Определить свойства параметры
- Определить в каком графическом виде, должно быть представлено решение.
FlexPDE - Система обозначений
В большинстве случаев, нотация в пакете FlexPDE использует обычный текст, как в языках программирования.
Например, дифференцирование обозначается в виде dx (..). Программа различает все названия координат, так же как и обозначения вторых производных dxx (..) и векторных операторов div (дивергенция), grad(градиент), curl (ротор).
При этом программа не различает заглавные и строчные буквы: так К и к обозначают одно и тоже.
FlexPDE - Генерирование Сетки
Команда "run" из программного меню FlexPDE начинает расчеты, автоматически создавая сетку конечных элементов, заполняющую описанную пользователем область решений. В этой сетке размер ячеек определяется расстоянием между отдельными заданными точками на границе области или кривизной дуг.
Возможный вид сетки для упорного газостатического подшипника с дискретными питателями
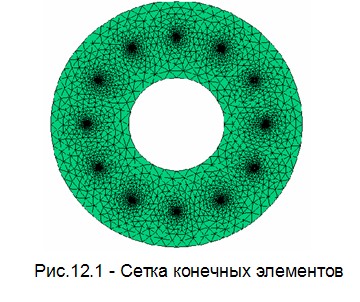
12.1 Программа расчета УГСП в среде Flex.PDE.
Предложенный метод расчета реализован в среде Flex.PDE в виде программы BIARING1R.PDE. Программа включает в себя разделы:
- variables (переменная) с переменной temp (безразмерный квадрат давления в зазоре)
- select в данном разделе задается число шагов для вычисления функций задаваемых оператором stages
- definitions в разделе задаются: Pa- давление на кромке подшипника,Ps- давление наддува, Rn- наружный радиус подшипника,Rv- внутренний радиус подшипника, Rd- радиус окружности расположения питателей, dp- диаметр питателей, Н- величина зазора подшипника, k1- покозатель адиабаты газа, ass- скорость звука, А- площадь питателей,
Gamma- конструктивный параметр, N- число питателей.
- equations в разделе приводится уравнения Рейнольдца при этом правая часть уравнения определяет влияние вращения на распределение давления в зазоре при sigma = 0 вращение отсутствует.
- boundaries в разделе строится смазываемая поверхность опоры УГСП обозначенная как Region 1, и задаем граничные условия на кромках подшипника Pa^2.
- monitors в разделе происходит отслеживание результатов расчетов в процессе работы программы.
- plots в разделе показаны конечные результаты численных значений в виде поля давлений (contour (p)).
- summary значений в определенных точках (report (p)).
- history команда связанная с Region.
Программа расчёта упорного газостатического подшипника созданная в среде Flex.PDE.
{BIARING1R .PDE }
{ **************************************************************
This problem
-- Submitted by Luis Zapata
************************************************************** }
title "pole davlenii i nesyhaya sposobnost"
Variables
temp { bezrazmerniy kvadrat davleniy v zazore }
stages=9
definitions
Par=0.98e5 {davlenie na kromke podshipnika , n/m2 }
Psr=4.9e5 {davlenie nadduva, n/m2 }
Rnr=0.112 {narushny radius podshipnika ,m}
Rvr=0.042 {vnutrenniy radius podshipnika , m}
Rdr=0.08 {radius okrushnosti raspoloshniy pitateley ,m}
dpr=0.6e-3 { diametr pitateley, m}
H=30e-6 { velichina zazora podchipnika, m }
A=if (pi*dpr*dpr/4
W=0
N=8 {chislo pitateley}
k1=1.4 {pokazatel adiabaty gaza }
F1=(2/(k1+1))^(2*k1/(k1-1))
F2=sqrt(2/(k1-1))*(2/(k1+1))^(-(k1+1)/(k1-1)/2)
Pa=Par/Psr
k=0.5
!k=staged(0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)
Pd=SQRT(k*(1-Pa^2)) {davlenie na kromke pitately}
Rn=1
Rv=Rvr/ Rnr {cm Rod radius}
Rd=Rdr/Rnr
dp=dpr/Rnr
p=abs(temp)^(1/2)
sigma=staged (0,1,2,3,4,5,6,7,9)
Qfi=-dx( p)*y+dy( p)*x
F3=(abs(temp^(1/k1))-abs(temp^((k1+1)/(2*k1))))^(1/2)
qf=if (temp
equations {define the heatflow equation }
div(grad(temp)) =sigma* Qfi
boundaries
Region 1 { the outer boundary defines the copper region }
start (0,-Rn)
value (temp) =Pa ^2 {convection boundary}
arc(center=0,0) angle 360
start (0,-Rv)
value (temp) =Pa ^2
arc(center=0,0) angle 360
repeat i=0 to 11{ an indexed loop on X-position } { an array of circular dots at the tabulated coordinates: }
start (Rd*sin(2*pi/N*i)+ dp,Rd*cos(2*pi/N*i))
value (temp) =Pd^2
arc(center=Rd*sin(2*pi/N*i),Rd*cos(2*pi/N*i)) angle=360
endrepeat
monitors
grid(x,y) zoom(-1,-1,2,2)
contour(p)
plots
grid(x,y)
contour(p)
contour(p) zoom(-1,-1,2,2)as "pole davlenii"painted
report (Rnr^2*Psr*INTEGRAL(p-Pa))report( sigma)
surface(p)zoom(-1,-1,2,2) as "pole davlenii"painted report( sigma)
elevation(p) from ( Rv,0) to ( Rn,0) report( sigma)
elevation(qf) from ( Rv,0) to ( Rn,0) report( sigma)
elevation(p) from Rv*cos(2*pi/N/2),Rv*sin(2*pi/N/2))
to ( Rn*cos(2*pi/N/2),Rn*sin(2*pi/N/2)) report( sigma)
summary
report( sigma)
report (Psr*(Rnr^2)*(INTEGRAL(p-Pa)))
report (INTEGRAL(p))
report (INTEGRAL(p-Pa))
histories
history(Psr*(Rnr^2)*(INTEGRAL(p-Pa))) versus sigma
history(Psr*(Rnr^2)*(INTEGRAL(p-Pa))) versus k
END 31705042
|



