10. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными граничными условиями. МКЭ основывается на методе взвешенных невязок, суть которого заключается в подборе функции, удовлетворяющей дифференциальным уравнениям и граничным условиям. Функция подбирается не произвольно, поскольку такой подбор вряд ли возможен уже в двухмерном пространстве, а с использованием специальных методов.

Пусть состояние некоторой среды описывается дифференциальным оператором LV+ P =0 с заданными граничными условиями V(Г)= Vг, где L - дифференциальный оператор (например оператор Лапласа), V - фазовая переменная -неизвестная функция, которую следует найти, Р - величина, независящая от V.

V(Г)=Vг -граничное условие первого рода (Дирихле), то есть на границе задано значение фазовой переменной. Будем искать решение с помощью функции,
имеющей вид:

где V* - приближенное решение, F- функция, удовлетворяющая граничным условиям,
N _m – пробные функции, которые на границе области должны быть равны нулю,
А _m – неизвестные коэффициенты, которые необходимо отыскать из условия наилучшего удовлетворения дифференциальному оператору, m- количество пробных функций. Если подставить V* в исходный дифференциальный оператор, то получим невязку, принимающую в различных точках области разное значение

Необходимо сформулировать условие, позволяющее минимизировать эту невязку по всей области. Одним из вариантов такого условия может быть уравнение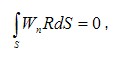

где W _n - некоторые весовые функции, в зависимости от выбора которых различают варианты метода взвешенных невязок, S- область пространства, в которой ищется решение.

При выборе в качестве весовых функций дельта-фукций получим метод поточечной коллокации, для кусочно-постоянных функций - метод коллокации по подобластям, но наиболее распространенным является метод Галёркина, в котором в качестве весовых функций выбираются пробные функции N. В этом случае, если количество пробных функций равно количеству весовых функций, после раскрытия определенных интегралов приходим к замкнутой системе алгебраических уравнений относительно коэффициентов А

где коэффициенты матрицы К и вектора Q вычисляются по формулам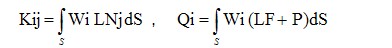

После нахождения коэффициентов А и подстановки их в (10.1), получим решение исходной задачи. Недостатки метода взвешенных невязок очевидны. Поскольку решение ищется сразу по всей области, то количество пробных и весовых функций должно быть значительным для обеспечения приемлемой точности, но при этом возникают трудности при вычислении коэффициентов Kij и Qi, особенно при решении плоских и объемных задач, когда потребуется вычисление двойных и тройных интегралов по областям с криволинейными границами. Поэтому на практике этот метод не использовался, пока не был изобретен метод конечных элементов (МКЭ).

Идея метода заключается в том, чтобы в методе взвешенных невязок воспользоваться простыми пробными и весовыми функциями, но не во всей области S, а в её отдельных подобластях (конечных элементах), при этом точность решения задачи обеспечить использованием большого числа конечных элементов (КЭ). Сами КЭ могут быть простой формы и вычисление интегралов по ним не должно вызывать особых затруднений. Математически переход от метода взвешенных невязок к МКЭ осуществляется с использованием специальных пробных функций, которые также называются глобальными базисными функциями, обладающих следующими свойствами:
1) в узле аппроксимации функции имеют значение равное единице;
2) отличны от нуля только в КЭ, содержащих этот узел аппроксимации, во всей остальной области равны нулю.
Далее рассматривается решение задач в одномерной области. Для одномерной задачи набор таких кусочно-линейных функций, при количестве КЭ, равном трем, иллюстрируется рисунком (рис.12.).

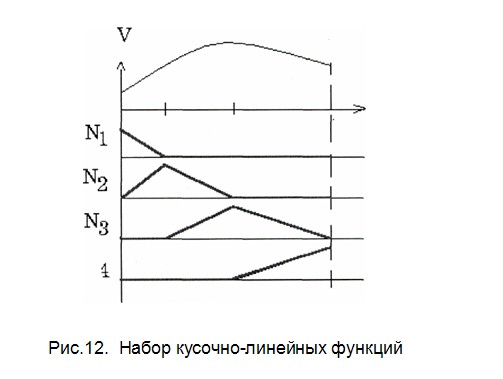В результате на каждом КЭ действует строго определенное число ненулевых глобальных базисных функций ( в данном примере две) и вместо вычисления интеграла по всей области можно вычислить интегралы по КЭ и сложить их. Процедура сложения получила название ансамблирование. Использование глобальных базисных функций приводит к тому, что процедура вычисления интегралов по КЭ становиться достаточно простой и, поскольку в узлах аппроксимации Nm=1, коэффициенты А приобретают физический смысл, они становятся равными значению фазовой переменной в узлах. В аппроксимации (2.22) теперь можно отказаться от использования функции F, поскольку удовлетворить граничные условия можно естественным образом, задавая значения V в узлах, расположенных на границе. В пределах одного КЭ, при условии, что он включен между i-м и j-м узлами, аппроксимацию решения можно определить с помощью глобальных базисных функций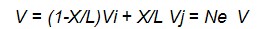

где Х- текущая координата, отсчитываемая от начала КЭ, L- его длина, Vi и Vj - значения фазовых переменных в узлах КЭ.

Компоненты вектора Ne получили название функций формы конечного элемента. Функции формы можно получить и из других соображений. Зададимся полиномом, аппроксимирующим решение внутри конечного элемента, например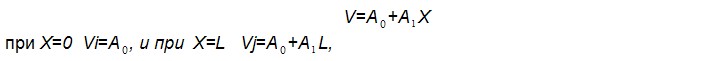

Находим коэффициенты А ₀ и А ₁ и подставляем их в аппроксимацию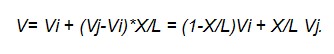

Таким же образом можно получить функции формы для квадратичной, кубической и других аппроксимаций. Соответственно аппроксимации называются и функции формы КЭ - квадратичный, кубический и т.д.
Решения задачи методом конечных элементов можно разбить на несколько этапов.

Этап 1. Выбор конечного элемента. В двухмерной задаче конечным элементом может быть треугольный (симплекс) элемент, четырехугольный элемент и в общем случае любая фигура, с помощью которой можно разбить исследуемую область на непересекающиеся подобласти. При разбиении области на конечные элементы следует учитывать, что чем сложнее элемент, тем с большими сложностями придется столкнуться при вычислении интегралов. Наиболее распространенными являются треугольный и четырехугольный элементы со сторонами параллельными осям координат. Для трехмерной области - тетраэдр и параллелепипед.

Этап 2. Разбиение области на КЭ. В отличие от метода конечных разностей разбиение может быть неравномерным и априорно учитывать градиент фазовой переменной, то есть там, где предполагается быстрое изменение фазовой переменной сетка должна быть гуще и наоборот. Существуют различные способы автоматического разбиения области на конечные элементы, поскольку исполнение этого этапа вручную может привести к существенным ошибкам.

Этап 3. Получение функции формы. Этот этап для нашей задачи уже был проделан для линейной функции формы. Можете получить квадратичную функцию формы, при этом, естественно должно использоваться три узла аппроксимации, один из которых является внутренним для КЭ. При расположении внутреннего узла в середине КЭ (что необязательно) должна получиться следующая аппроксимация: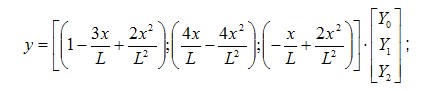

Этап 4. Получение матрицы жесткости и вектора нагрузок. Этот этап получил свое название из строительной механики, поскольку именно там впервые был применен МКЭ. На этом этапе используется метод взвешенных невязок в пределах одного КЭ. Согласно методу Галеркина необходимо вычислить определенный интеграл: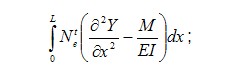

где L - длина КЭ.

Для Y- должно быть использовано аппроксимирующее выражение с использованием функций формы. Но здесь следует обратить внимание на соответствие порядка аппроксимирующего полинома и порядка исходного дифференциального уравнения. Порядок аппроксимирующего полинома должен быть больше или равен порядку дифференциального уравнения, чтобы существовала старшая производная, но существует способ понизить требование к гладкости аппроксимирующего полинома раскрыв интеграл по частям: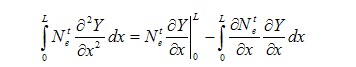

Проделав необходимые преобразования, получим следующую математическую модель КЭ: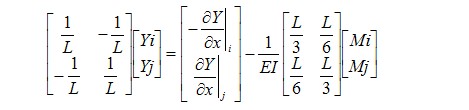

Раскрытие интеграла по частям привело еще к одному замечательному результату - в математической модели элемента появились производные фазовой переменной на границах элемента, это позволит в дальнейшем учесть граничные условия второго рода (типа Неймана).

Этап 5. Ансамблирование или получение глобальных матрицы жесткости и вектора нагрузок. Вектор неизвестных составляют прогибы в узлах, то есть матрица коэффициентов будет иметь четвертый порядок. Рассматривая поочередно каждый КЭ, располагаем элементы локальной матрицы жесткости в соответствии с номерами узлов подключения КЭ.

Этап 6. Учет граничных условий. Количество неизвестных в полной математической модели равно шести при четырех уравнениях, но учитывая, что Y(0) =0 и первая производная в нулевом узле также равна нулю, получаем замкнутую систему уравнений.

Этап 7. Решение системы алгебраических уравнений. При решении может быть учтена особенность матрицы коэффициентов, поскольку она, как правило, имеет ленточную форму.

В настоящее время имеется множество программ для ЭВМ, где реализован метод конечных элементов. Мы использовали пакет Flex.PDE, в котором составлена программа, позволяющая определить поле давлений в зазоре подшипника, как при неподвижных поверхностях, так и при их относительном вращении.