|
7. Зависимость прочности КМ от объемной концентрации волокон
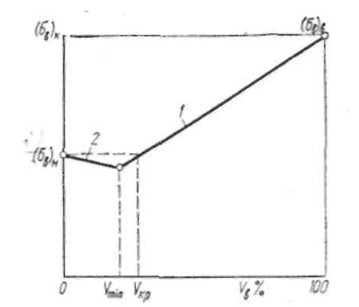
Рисунок 5. Зависимость прочности однонаправленных КМ от объемной концентрации волокон: 1 – по уравнению (1); 2 – по уравнению (2)
На рисунке построен график зависимости прочности КМ от объемной концентрации волокон по уравнению (1)–прямая 1 и прямая 2–по уравнению (2).
Объемная доля волокон соответствующая точке пересечения этих прямых, называется минимальной объемной концентрацией волокон  . Ей соответствует минимальная прочность КМ. . Ей соответствует минимальная прочность КМ.
Если  , прочность композиции уменьшается пропорционально увеличению объемной доли волокон, а при , прочность композиции уменьшается пропорционально увеличению объемной доли волокон, а при  возрастает. возрастает.
Из (3) соотношения видно, что для сильно упрочняющих матриц( велико) велико) будет большим. Напротив, если деформационное упрочнение матрицы отсутствует ( будет большим. Напротив, если деформационное упрочнение матрицы отсутствует ( ),то и ),то и  . Минимальная объемная доля волокон . Минимальная объемная доля волокон  уменьшается также по мере повышения прочности последних. уменьшается также по мере повышения прочности последних.
При армировании волокнами основная цель состоит в том, чтобы получить композицию, прочность которой превышает прочность матрицы:
 . .
Это соотношение определяет критическую объемную долю  , которую следует превысить для получения композиции с прочностью : , которую следует превысить для получения композиции с прочностью :
 . .
Критической объемной долей  - называют такую объемную долю волокон, при которой прочность КМ равна прочности неармированной матрицы. - называют такую объемную долю волокон, при которой прочность КМ равна прочности неармированной матрицы.
Из этой формулы следует ,что чем больше разница в прочностных свойствах волокон и матрицы , тем меньше критическая объемная доля  , которая может изменяться в широких пределах –от 1 до 50%. , которая может изменяться в широких пределах –от 1 до 50%.
Таблица 2. Значения Kmin об. % для композиций на основе Al, Си, Ni и нержавеющей стали.
Для более рационального армирования желательно : значения  и и  иметь как можно меньшими, чтобы достигнуть упрочнения при небольшой объемной доле волокон. На практике этого добиваются, вводя в матрицу волокна с пределом прочности, значительно превышающим иметь как можно меньшими, чтобы достигнуть упрочнения при небольшой объемной доле волокон. На практике этого добиваются, вводя в матрицу волокна с пределом прочности, значительно превышающим  (величина (величина  для пластичных матриц обычно близка к их пределу текучести). для пластичных матриц обычно близка к их пределу текучести).
Расчетные данные о минимальной объемной доле волокон для композиций на основе Al,Си,Ni и нержавеющей стали, армированных проволоками с различным пределом прочности, приведены в табл. 2. При низкой прочности волокон  может превышать 50 об.%. может превышать 50 об.%.
Механизм разрушения композиций при  может отличаться от такового при может отличаться от такового при  . В случае . В случае  прочность всего материала контролируется прочностью волокон и разрушение даже небольшой их части вызывает, согласно рассматриваемой модели , катастрофическое разрушение матрицы и всей композиции. прочность всего материала контролируется прочностью волокон и разрушение даже небольшой их части вызывает, согласно рассматриваемой модели , катастрофическое разрушение матрицы и всей композиции.
Если же  и пластичная матрица способна испытывать деформационное упрочнение при растяжении, то разрыв волокон не приводит к немедленному разрушению материала. В момент разрыва
волокон напряжение падает, но при дальнейшем нагружении матрица деформационно упрочняется и нагружает разрушенные волокна. В результате нагрузка восстанавливается до прежнего уровня. Вся композиция раз
рушится только после того, как исчерпается запас пластичности матрицы. Иначе говоря, общая деформация материала контролируется пластическими свойствами матрицы. При этом в процессе нагружения волокна многократно разрываются по длине. и пластичная матрица способна испытывать деформационное упрочнение при растяжении, то разрыв волокон не приводит к немедленному разрушению материала. В момент разрыва
волокон напряжение падает, но при дальнейшем нагружении матрица деформационно упрочняется и нагружает разрушенные волокна. В результате нагрузка восстанавливается до прежнего уровня. Вся композиция раз
рушится только после того, как исчерпается запас пластичности матрицы. Иначе говоря, общая деформация материала контролируется пластическими свойствами матрицы. При этом в процессе нагружения волокна многократно разрываются по длине.
|




 . Ей соответствует минимальная прочность КМ.
. Ей соответствует минимальная прочность КМ.
 , прочность композиции уменьшается пропорционально увеличению объемной доли волокон, а при
, прочность композиции уменьшается пропорционально увеличению объемной доли волокон, а при  возрастает.
возрастает.
 велико)
велико) ),то и
),то и  . Минимальная объемная доля волокон
. Минимальная объемная доля волокон  .
.
 , которую следует превысить для получения композиции с прочностью :
, которую следует превысить для получения композиции с прочностью :
 .
.

 (величина
(величина  может отличаться от такового при
может отличаться от такового при  . В случае
. В случае