Сопротивление материалов  

Лабораторная работа № 8

Исследование нормальных напряжений при изгибе балкиравного сопротивления.

Цель работы: Экспериментально исследовать характер распределения нормальных напряжений по длине балки при плоском изгибе; сравнение полученных результатов с теоретическими значениями.

8.1. Общие сведения

Изгибу подвергается консольная балка равного сопротивления, по-перечное сечение которой – прямоугольник с изменяющейся по длине балки шириной b(z) (рис. 8.1).

Балка равного сопротивления изгибу – это балка, у которой во всех поперечных сечениях наибольшее нормальное напряжение одинаково. Такие балки применяются для экономии материала, либо для увеличения гибкости.
Наибольшее нормальное напряжение в произвольном сечении A-A с координатой Z определяется по формуле:

σ(z) = Mx(z) / Wx(z)                                        (8.1)

где Mx(z) – изгибающий момент сечения A-A:

Mx(z) = P · z                                        (8.2)

      Wx(z) = P · z – осевой момент сопротивления поперечного сечения относительно оси X:

Wx(z) = b(z) · h2 / 6                                        (8.3)

      b(z) - ширина сечения; изменяется по длине балки по линейному закону и связана с координатой сечения Z зависимостью:

b(z) = b · z / l                                        (8.4)

      h(z) – высота сечения, постоянная по всей длине балки.

Подставив выражения (8.2), (8.3), (8.4) в (8.1), получим формулу для определения нормального напряжения исследуемой балки равного сопротивления:

σ = (P · 6 · l) / ( b · h2 )                                        (8.5)

Из формулы (8.5) следует, что наибольшие нормальные напряжения в сечениях балки равного сопротивления одинаковы (не зависят от координаты сечения) и связаны с нагрузкой P линейной зависимостью.


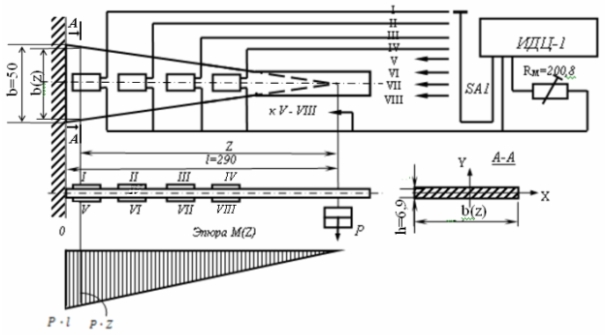
Рис. 8.1

8.2. Описание экспериментальной установки.

Для измерения нормальных напряжений в сечениях балки равного сопротивления используется метод электрического тензометрирования. На исследуемую балку в разных сечениях наклеены 8 тензорезисторов; схема их расположения показана на рис. 8.1. Четыре из них (I-IV) регистрируют деформации растяжения в верхних волокнах балки, четыре других (V-VIII) – деформации сжатия в нижних волокнах.

Каждый из тензометров с помощью переключателя SA1 может быть включен в состав измерительной полумостовой схемы. Вторым плечом полумоста является магазин сопротивлений. Сопротивление магазина RМ =200,8 Ом соответствует паспортному сопротивлению регистрирующих тензорезисторов.

Измерительный полумост подключен к разъему первого канала циф-рового измерителя деформации марки ИДЦ-I. Измеритель деформации работает по принципу автоматической балансировки измерительного моста. Факт балансировки регистрируется зажиганием цифровых индика-торных ламп. Цифровая шкала прибора отградуирована в ЕОД – единицах относительной деформации. Цена деления (единицы) цифрового индика-тора – 10 ЕОД. Градуировка цифрового индикатора приведена к чувстви-тельности тензорезисторов К.

Показания цифрового индикатора до (ε0) и после (εP) нагружения балки нагрузкой P позволяют вычислить величину приращения относительной деформации в исследуемом сечении:

Δε = εP - ε0.                                        (8.6)

Для тензорезисторов с произвольным коэффициентом тензочувствительности К относительная деформация равна:

εц = 2 / K · Δε (ЕОД), или εц = (2 · Δε) / (K · 106) = Δε · 10-6.                                        (8.7)

Измерив относительную деформацию, определяем нормальные напряжения по закону Гука:

σ(z) = E · ε .                                        (8.8)

При проведении измерений принять: коэффициент тензочувствительности используемых тензометров К = 2,1; модуль упругости материала балки Е = 2· 105 МПа.
Тогда получим формулы для определения значений относительной деформации и нормального напряжения в виде:

εц = 0,95 · Δε (ЕОД), или εц = 0,95 · 10-6 · Δε.                                        (8.9)

σ = 0,19 · Δε (МПа) = 1,9 · Δε (кг/см3).                                        (8.10)

8.3. Порядок выполнения работы

8.3.1. Включить установку в сеть и нажать кнопку «ПИТАНИЕ». Вольтметр ИДЦ должен показывать 12 В.
8.3.2. Ручками магазина сопротивлений установить RМ = 200,8 Ом.
8.3.3. Утопить кнопку первого канала ИДЦ. Остальные кнопки каналов должны быть отжаты.
8.3.4. С помощью переключателя требуемый тензорезистор включить в измерительный полумост.
8.3.5. Кратковременным нажатием кнопки «ПУСК» провести измерение. Записать показания цифрового табло Ε0 для каждого тензометра в таблицу 8.1.
Для получения стабильных результатов перед измерениями рекомендуется произвести несколько запусков ИДЦ и вращений переключателя каналов вправовлево в пределах хода.
8.3.6. Повторить измерения деформаций при нагрузках Р = 5 кг и Р = 10 кг для каждого тензометра. Результаты записать в табл. 8.1.
8.3.7. Разгрузить балку. Выключить установку.
8.3.8. По формуле (8.6) вычислить и записать в табл. 8.1 разности отсчетов Δε - приращения деформаций под действием нагрузок.
8.3.9. По формуле (8.10) для всех сечений и нагрузок вычислить и записать в табл. 8.2 экспериментальные значения нормальных напряжений.
8.3.10. По формуле (8.5) определить теоретические знания нормальных напряжений при P = 5 кг и P = 10 кг. Записать в табл. 8.2.
8.3.11. Для каждой ступени нагружения выявить сечение с наибольшей погрешностью определения нормального напряжения. Напряжение подчеркнуть. Погрешность вычислить по формуле:
δmax = (|δтеор - |δmaxтеор||) / δтеор
и вписать в табл. 8.2. 8.3.12. Построить графики распределения теоретического и экспериментального значений нормальных напряжений по длине балки равного сопротивления изгибу.
8.5. Образец отчета
Лабораторная работа №8
Исследование нормальных напряжений при изгибе балки равного сопротивления


8.5.1. Цель работы:
8.5.2. Испытательная установка (рис.8.1).
8.5.3. Результаты измерений и вычислений деформаций

Таблица 8.1

№ тенз. Относительная деформация (ЕОД)
Р = 0 кг Р = 5кг = 50Н Р = 10кг = 100Н
отсчёт ε0 отсчёт εp разность отсчётов Δε отсчёт εp разность отсчётов Δε
I          
II          
III          
IV          
V          
VI          
VII          
VIII          

8.5.4.Определение теоретических и экспериментальных значений нормальных напряжений:
σтеор = P · (6 · l) / (b · h2)
σэксп i = 0,19 · Δεi (МПа) = 1,9 · Δεi (кг/см2).

Таблица 8.2

Нагрузки, Н Нормальные напряжения, МПа δmax,%
теоретические экспериментальные
σ σI σII σIII σIV σV σVI σVII σVIII  
50                    
100                    

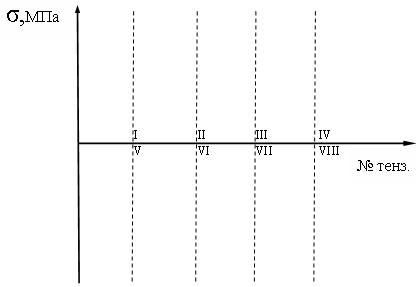
8.5.5 Графики нормальных напряжений
8.5.6. Выводы:

Работу принял______________
«_____»____________200___г.

Примечание: в выводах необходимо отметить:
                        а) как распределяются нормальные напряжения по длине балки равного сопротивления изгибу;
                        б) как зависят нормальные напряжения от величины нагрузки P;
                        в) какова максимальная погрешность между теоретическими и экспериментальными значениями нормальных напряжений.

7.6.Контрольные вопросы
  1. Что называется балкой равного сопротивления изгибу?
  2. Где используются балки равного сопротивления и почему?
  3. Каков закон распределения максимальных нормальных напряжений по длине балки?
  4. Что и в каких единицах регистрирует прибор ИДЦ-I ?
  5. Какой принцип реализован в работе прибор ИДЦ-I ?