Сопротивление материалов  

Лабораторная работа №7

Определение перемещений балки при плоском изгибе

Цель работы: экспериментальное определение линейных и угловых перемещений двухопорной балки и сравнение их с теоретическими значениями, полученными с использованием ЭВМ.

7.1. Общие сведения

При действии на балку внешних сил в плоскости одной из главных центральных осей инерции сечения ось балки искривляется в той же плоскости. Такой изгиб называют плоским изгибом. Искривлённую ось балки называют изогнутой осью или упругой линией.

При изгибе имеют место два вида перемещений поперечного сечения балки: линейное – прогиб «Y» и угловое – угол поворота «θ» (рис. 7.1). Теоретически перемещения сечений балки определяют методом интегрирования приближённого дифференциального уравнения упругой линии, методом начальных параметров, методом Мора, способом Верещагина.


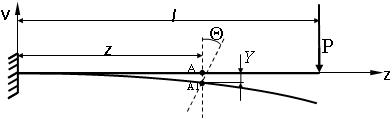
Рис. 7.1

В данной работе необходимо определить прогибы и углы поворота сечений двухопорной балки с консолью при различном приложении сосредоточенной нагрузки на консоли и в пролёте.

Расчётная схема балки представлена на рис. 7.2. Прогибы определяются в точке А с координатой ZA на консоли и в точке С с координатой ZC в пролёте, углы поворота определяются в точках В и Е на опорах балки.


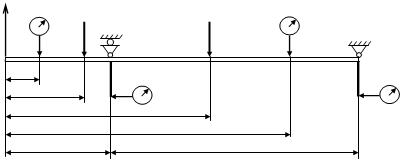
Рис. 7.2

Любой из теоретических методов даёт для определения перемещений заданных сечений балки следующие формулы:

  1. Сила Р действует на консоли ( 0 < b < a )



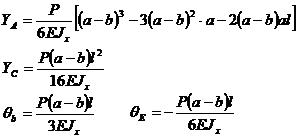
    (7.1)





  2. Сила Р действует в пролёте ( a < b < a+l )









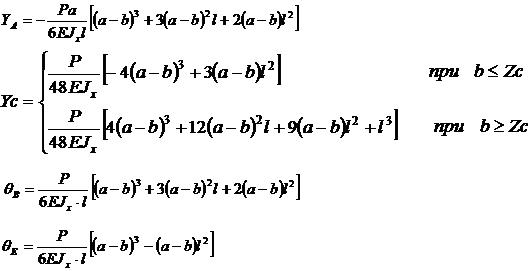
    (7.2)






где: b –расстояние от начала координат до точки приложения силы P, может принимать любое значение в пределах 0 < b < a ;
       E - модуль упругости материала балки;
       Jx – осевой момент инерции поперечного сечения балки.

7.2. Описание испытательной установки

Для проведения работы используется испытательная установка, представленная на рис. 7.3. Установка состоит из исследуемой балки 1, основания 2, подвижной 3 и неподвижной 4 опор, двух индикаторных стоек 5, гиревого подвеса 6, набора грузов 7, индикаторов часового типа 8.

Исследуемая балка изготовлена из стальной полосы (модуль упругости E = 2·105 МПа) прямоугольного поперечного сечения (ширина B = 40мм, высота H = 7мм) и установлена на шарнирных опорах. Длина пролёта l = 700мм, длина консоли a = 300мм. Эти параметры можно изменять в пределах полной длины балки (l + a = 1000мм).

Нагружение балки сосредоточенной силой осуществляется с помощью гиревого подвеса и набора грузов. Изменение точки приложения нагрузки осуществляется перемещением гиревого подвеса по балке. Определение расстояний b от левого конца балки (начала координат) до точки приложения нагрузки производится по шкале, нанесённой на поверхности балки.

Перемещения балки можно определять для случаев приложения нагрузки на расстояниях от начала координат b = 0, 100, 200мм (на консоли) и b = 400, 500, 600, 700, 800, 900мм (в пролёте) – это отметки 0, 10, 20, 40, 50, 60, 70, 80, 90 на балке. Возможны и другие значения расстояний b в пределах длины балки.


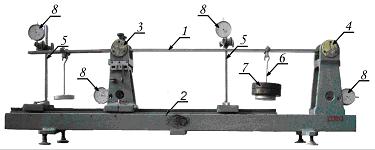
Рис. 7.3

При проведении эксперимента количество точек приложения нагрузки может быть уменьшено и может не совпадать с количеством таких точек при теоретическом определении перемещений. Измерение прогибов и углов поворота опорных сечений балки производится с помощью индикаторов часового типа с ценой деления 0,01мм.

Прогибы измеряются непосредственно по показаниям индикаторов. Углы поворота на опорах измеряются при помощи стержня ВК, перпендикулярного оси балки и жёстко соединённого с опорами (рис. 7.2. и 7.4.). При повороте сечения на некоторый угол θ, на такой же угол повернётся стержень (рис. 7.4.). Индикатор, установленный на расстоянии ВК=L=150мм от оси балки, показывает при этом линейное перемещение

КК1 = ΔТ = L · tgθ.
Деформации балки малы, поэтому tgθ ≈ θ и углы поворотов можно определять по формуле:

θ ≈ ΔT / L

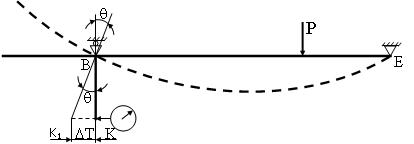
Рис. 7.4

7.3. Порядок проведения работы

7.3.1. Установить призму с гиревым подвесом на расстоянии b от начала координат (от левого конца балки).
7.3.2. Установить большие стрелки всех индикаторов на «0» и записать показания Т0 в соответствующей графе таблицы 7.1. Индикаторы №1 и №3 служат для определения прогибов, а №2 и №4 – для определения углов поворотов сечений балки.
7.3.3. Нагрузить балку силой Р = 20Н, устанавливая грузы на подвес.
7.3.4. Записать показания индикаторов в табл. 7.1.
7.3.5. Разгрузить балку.
7.3.6. Прикладывая нагрузку на консоли и в пролёте при разных значениях b, повторить опыты по п. 7.3.2. – 7.3.5. Для сокращения времени на проведение эксперимента количество точек приложения нагрузки может быть меньше десяти (тогда в табл. 7.1. могут быть заполнены не все строки).
7.3.7. Вычислить разности показаний индикаторов ΔТ и определить прогибы и углы поворота сечений балки
YА = ΔТ1,       YC = ΔТ3
θВ = ΔT2 / L,       θE = ΔT4 / L.

Результаты вычислений записать в табл. 7.2.
Сравнить значения перемещений сечений балки при изменении точки приложения нагрузки. Табл. 7.2. должна содержать столько строк, сколько было заполнено в табл. 7.1. при проведении эксперимента.

7.3.8. Определить теоретические значения прогибов и углов поворота в рассматриваемых сечениях по формулам (7.1) и (7.2) с помощью ЭВМ (см. п.7.4).Результаты вычислений записать в табл. 7.2.
7.3.9. Сравнить экспериментальные и теоретические значения перемеще-ний сечений балки, вычислив расхождения
где YТ, θТ – теоретические значения перемещений сечений;
      YЭ, θЭ – экспериментальные значения перемещений.
Результаты вычислений занести в табл. 7.2.
7.3.10. Построить графики зависимости перемещений от положения точек приложения нагрузки (формы упругой линии балки для разных значений расстояний bi). Сравнить с графиками, полученными на ЭВМ.
7.3.11. Оформить отчет по прилагаемой форме (см. п.7.5.).

7.4. Определение теоретических значений перемещений с использованием ЭВМ

По формулам (7.1.) и (7.2.) разработана программа расчёта перемещений в различных сечениях балки на ПК в зависимости от положения и величины нагрузки при различных значениях параметров a, l в пределах полной длины балки a + l = 1000мм.

Программа позволяет получить прогибы в любых точках балки вне опор и углы поворотов на опорах. Общее число точек приложения нагрузки - 10. По итогам расчёта программа выдает в виде таблицы значения перемещений (прогибов в точках A и С и углов поворота в точках В и Е) для десяти случаев нагружения балки.

Кроме этого программа для десяти случаев нагружения строит не-прерывные графики зависимости перемещений (YА, YС, и θВ, θЕ) от величины и расположения действующих нагрузок для всех 10 вариантов нагружения.

    Программа работает в операционной системе «Windows».
    Результаты расчетов и графики можно вывести на печать.

Порядок использования программы расчёта перемещений.
7.4.1. Включить ПК в сеть.
7.4.2. На рабочем столе монитора последовательно открыть папки «Мои документы», «Mechanics», «Sopromat», «lab 07».
7.4.3. В папке «lab 07» открыть файл «lab 07.exe». На экране появляется окно с названием работы «Определение перемещений при изгибе». Раз-вернуть окно. В окне представлены четыре вкладки для работы с про-граммой, расчётная схема балки и таблица для заполнения исходных данных. При этом активирована вкладка «Исходные данные».
7.4.4. Последовательно заполнить все строки таблицы согласно принятой схеме нагружения, например: а = 300мм, l = 700мм, Р = 10Н, ZA = 0, ZC = 650мм, b1 = 0, b2 = 100мм, b3 = 200мм, b4 = 400мм, b5 = 500мм, b6 = 600мм, b7 = 650мм, b8 = 700мм, b9 = 800мм, b10 = 900мм. При этом параметры a, l, ZA, ZC и некоторые значения bi должны совпадать с параметрами при проведении эксперимента.
7.4.5. Открыть вкладку «Графики и таблицы». В этом окне появляются цветные графики – формы упругой линии при заданной нагрузке в зависимости от координат точек приложения bi (i =1,2,…,10). Эти графики наглядно показывают зависимость прогибов балки от изменения точек приложения нагрузки.
Ниже графиков представлена таблица теоретических значений прогибов YА и YС в миллиметрах и углов поворота θВ и θE в радианах при заданных значениях координат bi.
7.4.6. Из таблицы перемещений выбрать те значения, которые соответствуют схеме, принятой при проведении эксперимента. Записать эти значения в табл. 7.2.
7.4.7. Распечатать графики на принтере.
7.4.8. Открыть вкладку «Зависимость Y от b». В этом окне представлены цветные графики зависимости прогибов YА (на конце консоли) и YС (посередине пролёта) от координат bi.
7.4.9. Открыть вкладку «Зависимость θ от b». В этом окне представлены графики зависимости углов поворота на опорах θВ и θE от координат bi.
7.4.10. Закрыть окно файла и предыдущих папок и выключить компьютер.

7.5. Образец отчёта
Лабораторная работа №7
Определение перемещений балки при плоском изгибе
7.5.1. Цель работы:
7.5.2. Схема нагружения балки (рис. 7.2)
7.5.3. Результаты испытаний и расчётов.

Таблица 7.1

Положение
нагрузки		 Номера и показания индикаторов в мм
1 2 3 4
№
п/п		 bi,
мм		 T0 T ΔT T0 T ΔT T0 T ΔT T0 T ΔT
1 0                        
2 100                        
3 200                        
4 400                        
5 500                        
6 600                        
7 650                        
8 700                        
9 800                        
10 900                        

7.5.4. Сравнение экспериментальных и теоретических значений перемещений.

Таблица 7.2

Положение
нагрузки		 YА, мм θВ, рад. YC, мм θE, рад.
bi,
мм		 эксп. теор. расх.,% эксп. теор. расх.,% эксп. теор. расх.,% эксп. теор. расх.,%
0                        
100                        
200                        
400                        
500                        
600                        
650                        
700                        
800                        
900                        

7.5.5. Форма упругой линии балки
7.5.6. Выводы:

Работу принял______________
«_____»____________200___г.

Примечание: в выводах необходимо отметить:
                        а) как изменяются перемещения сечений балки при изменении точек приложения нагрузки;
                        б) каковы расхождения расчётных и экспериментальных значений перемещений.

7.6.Контрольные вопросы
  1. Что называется упругой линией балки?
  2. Какие перемещения получают сечения балки при плоском изгибе?
  3. Какие существуют теоретические методы для определения прогибов и углов поворотов сечений балки?
  4. Как экспериментально определяются перемещения сечений балки?
  5. Как изменяются перемещения консольной части балки при изменении точки приложения нагрузки?
  6. Как изменяются перемещения в пролёте балки при изменении точки приложения нагрузки?