Сопротивление материалов  

Лабораторная работа №4

Исследование концентрации напряжений

Цель работы: Экспериментальное исследование распределения нормальных напряжений в поперечных сечениях полосы, ослабленной вырезами; определение теоретического коэффициента концентрации напряжений.

4.1. Общие сведения

При растяжении-сжатии стержня нормальные напряжения в любом поперечном сечении распределяются равномерно, если по длине поперечные сечения постоянны.
При резких изменениях формы или размеров поперечного сечения стержня (наличие поперечных отверстий, выточек, надрезов и т.п.) происходит неравномерное распределение напряжений в сечении, т. е. возникает концентрация напряжений – местное увеличение напряжений. Факторы, вызывающие концентрацию напряжений (отверстия, выточки, вырезы), называют концентраторами напряжений. Максимального значения напряжения достигают в области концентратора напряжений.
Количественной характеристикой концентрации напряжений является теоретический коэффициент концентрации ασ, равный отношению наибольшего местного напряжения σmax к номинальному напряжению σном.:

ασ = σmax / σном ,                                                    (4.1)

Номинальное напряжение σном – это напряжение, которое возникло бы в сечении, ослабленном концентратором, без учета эффекта концентрации.
Теоретический коэффициент концентрации показывает, во сколько раз увеличивается напряжение в зоне концентратора по сравнению с номинальным.
При растяжении полосы, ослабленной вырезами (рис. 4.1), напряжения в сечении 2-2 (достаточно удаленном от концентратора) распределяются равномерно; их вычисляют по формуле:

σ = P / F ,                                                    (4.2)

где F=F2 – площадь неослабленного сечения 2-2.

В сечении 1-1, ослабленном вырезами, напряжения распределяются неравномерно, возрастая к краям полосы и убывая к середине. Номинальное напряжение в ослабленном сечении равно:

σном = P / F1 ,                                                    (4.3)

где F1 – площадь ослабленного сечения 1-1.

               
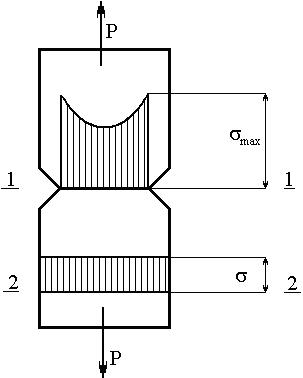
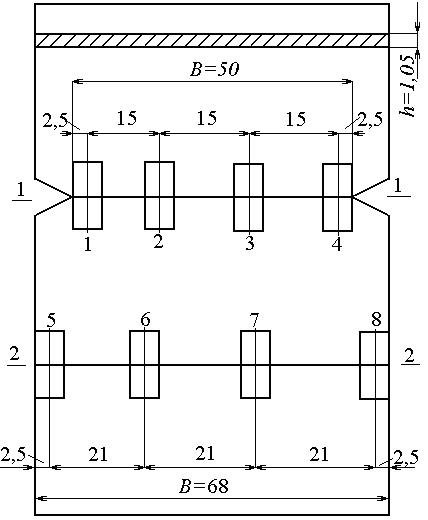
Рис. 4.1                                                              Рис. 4.2

Значения теоретического коэффициента концентрации напряжений &apha;σ приводятся в справочной литературе в зависимости от вида концентратора. Выбрав соответствующее значение теоретического коэффициента концентрации напряжении &apha;σ и определив номинальное напряжение &apha;ном, можно рассчитать наибольшее напряжение, которое возникает в ослабленном сечении:

σmax = ασ / σном ,                                                    (4.4)

4.2. Описание экспериментальной установки

Работа выполняется на универсальном прессе УП-5 (рис. 4.3). Пресс УП-5 состоит из станины 2, малого рычага 3, большого рычага с противовесами 4, подвески для гирь 5, набора гирь 6, зажимов для образца 7, механизма регулировки 8. В зажимах установлен объект испытаний – полоса с вырезами 1. Пресс УП-5 установлен на столе 9. Для определения напряжений в разных сечениях на полосу наклеиваются 8 электрических тензометров сопротивления. Размеры полосы и схема расположения тензометров указаны на рис. 4.2.

Электрические тензометры R1, …, R8 поочередно включают в полумостовую схему тензометрического усилителя УТ 4-1 (рис. 4.4) при помощи переключателя П. Другим плечом измерительного полумоста является магазин сопротивлений типа МСР-5. Усилитель УТ 4-1 имеет на выходе измерительный прибор (миллиамперметр), регистрирующий разбаланс измерительного моста, а следовательно, деформации в испытываемой полосе. По показаниям миллиамперметра определяют механические напряжения при помощи масштабного коэффициента.

      
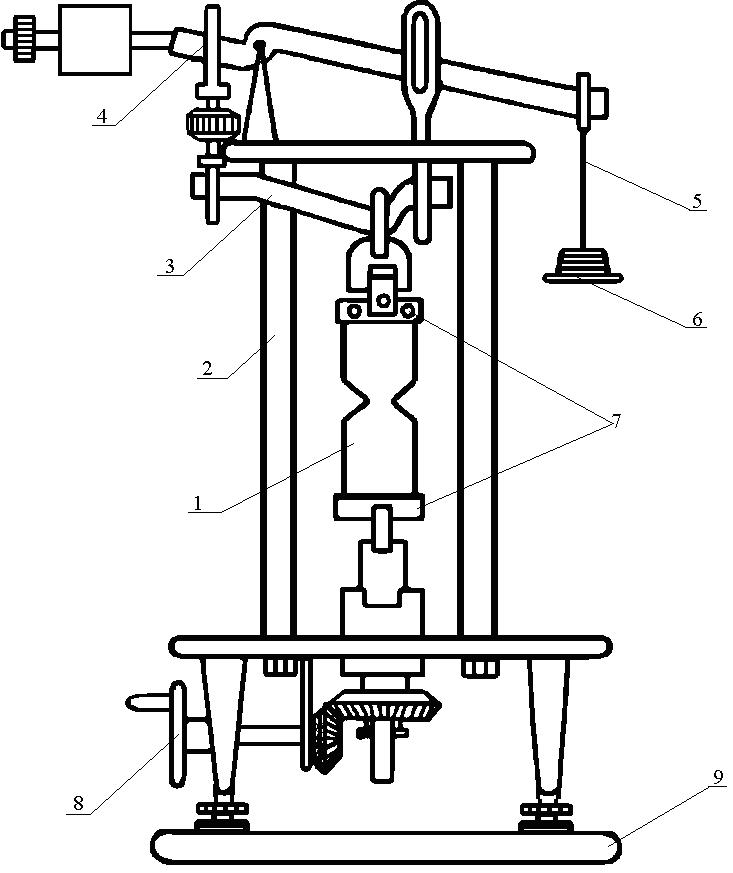
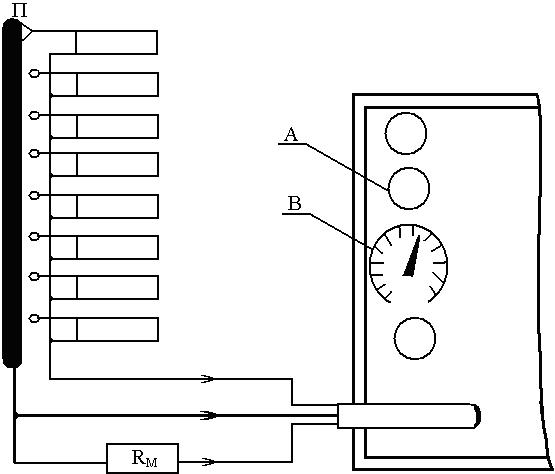
Рис. 4.3                                                     Рис. 4.4

4.3. Тарировка измерительного устройства

Для перевода показаний миллиамперметра в механические напряжения необходимо определить цену деления (масштаб) шкалы миллиамперметра. Для этого в одно из плеч измерительного моста (магазин сопротивлений) необходимо ввести дополнительное сопротивление ΔRT. Принимаем ΔRT = 0,1 Ом. Это вызовет разбаланс измерительного моста и соответствующее отклонение стрелки миллиамперметра ΔJT.
По величине калибровочного сопротивления ΔRT вычисляют величину механического напряжения, создающего такой же разбаланс измерительного моста:

σT = ΔRT · E / K · RM ,                                                    (4.5)

где RM = RT – сопротивление магазина сопротивлений, равное сопротивлению тензометра; К = 2,05 – коэффициент тензочувствительности тензометра; Е = 2·105 – модуль упругости материала полосы.

Масштаб μ шкалы миллиамперметра определяется по формуле:

μ = σT / ΔJT (МПа/mA),                                                    (4.6)

Зная масштаб, определяют механические напряжения в испытуемом образце

σ = μ · ΔJT (МПа),                                                    (4.7)

где ΔJ – отклонение стрелки миллиамперметра на одну ступень нагружения образца (ступень нагружения соответствует прикладываемой растягивающей силе).

4.4. Порядок проведения работы
4.4.1. Включить усилитель в сеть и прогреть его в течение 20-30 мин.
4.4.2. Нагрузить образец предварительной нагрузкой P0 =1 500 Н, для чего на подвес 5 пресса УП-5 установить гири массой 3 кг.
4.4.3. С помощью переключателя П (рис 4.4) подключить тензометр 1 к усилителю для тарировки миллиамперметра (тарировку можно производить на любом тензометре).
4.4.4. Установить сопротивление магазина RM = 200 Ом (в соответствии с паспортными данными тензометра) и вращением ручек А и В усилителя добиться того, чтобы стрелка миллиамперметра находилась в нулевом положении. Записать показание магазина сопротивлений RM = RT.
4.4.5. Увеличить сопротивление магазина на ΔRT = 0,1 Ом и записать показание миллиамперметра ΔJT.
4.4.6. Установить на магазине сопротивлений первоначальное сопротивление RM = 200 Ом и нулевой ток на миллиамперметре. Записать показания RM и J0 в табл. 4.2.
4.4.7. С помощью переключателя П (рис. 4.4) подключить поочередно тензометры 2, …, 8 к усилителю и, не вращая ручки А и В усилителя, установить минимальный ток миллиамперметра изменением сопротивления магазина RM. Записать в табл. 4.2 значения RM и J0 для всех 8 тензометров.
4.4.8. Нагрузить образец усилием Р = 5000 Н, для чего на подвес 5 установить гири массой 10 кг.
4.4.9. С помощью переключателя П подключить поочередно тензометры 1, …, 8 к усилителю, установить сопротивление магазина согласно табл. 4.2 для каждого тензометра и записать показания J миллиамперметра.
4.4.10. Повторить трехкратное нагружение и разгружение образца, делая записи соответствующих показаний в табл. 4.2.
4.4.11. Определить масштаб шкалы миллиамперметра: μ = σT / ΔJT =
4.4.12. По данным таблицы 4.2 определить для каждого тензометра:
а) средние значения показаний миллиамперметра, mA:
J0ср = (J01 + J02 + J03) / 3 = ,         Jср = (J1 + J2 + J3) / 3 = ,
б) среднее приращение тока, mA: ΔJ = Jср - J0ср = ,
в) величины механических напряжений, МПа: σ = μ · ΔJ = .
4.4.13. Определить номинальное напряжение в ослабленном сечении полосы:
σном = (P - P0) / (b · h), МПа
где P - P0 = 3500 Н – ступень нагружения образца.
4.4.14. Построить эпюры напряжений в сечениях 1-1 и 2-2, как показано на рис. 4.5. Эпюры напряжений в крайних точках сечений необходимо достроить, продолжая графики, построенные по данным таблицы 4.2.
4.4.15. По графикам напряжений в сечении 1-1 (с учетом масштаба чертежа) определить σmax1 и σmax1.

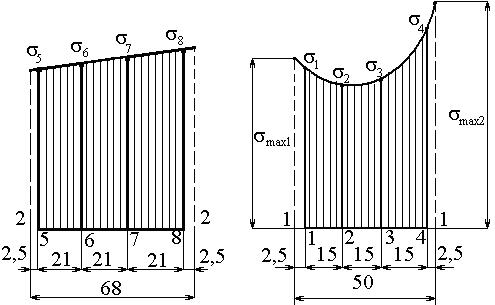
Рис. 4.5

4.4.16. Определить значения теоретического коэффициента концентрации в зоне каждого выреза полосы:
ασ1 = σmax1 / σном          ασ2 = σmax2 / σном
4.4.17. Оформить отчет по прилагаемой форме.

4.5. Образец отчета
Лабораторная работа №4
Исследование концентрации напряжений

4.5.1. Цель работы:
4.5.2. Испытательная установка:
Универсальный пресс УП-5, магазин сопротивлений МСР-5, тензометрический усилитель УТ 4-1.
4.5.3. Схема установки электрических тензометров (рис. 4.3) и размеры полосы
Толщина полосы h, мм 1,05
Ширина полосы в неослабленном сечении b, мм 68
Ширина полосы в ослабленном сечении b, мм 50
Площадь в неослабленном сечении F2, м2  
Площадь в ослабленном сечении F1, м2  

4.5.4. Тарировка (определение масштаба шкалы миллиамперметра усилителя):
RM = RT =     (Ом),
ΔRT =     (Ом),
ΔJT =     (mA),
Е = 2 · 105     (МПа),
К = 2,05.

Тарировочное напряжение: σT = (ΔRT · E) / (K · RM) =    (МПа).
Масштаб шкалы миллиамперметра: μ = σT / ΔJT   (МПа/mA).

Таблица 4.2

Результаты испытаний и расчетов
№тен
зо
мет
ра		 RM,
Ом		 P0=1500 Н P=1200 кг (12 кН)7 ΔJ = Jср - J0ср,
mA		 σ = μ · ΔJср,
МПа
JP0, mA JP0ср, mA J, mA JPср, mA
1 2 3 1 2 3
повторности повторности
1                      
2                      
3                      
4                      
5                      
6                      
7                      
8                      

4.5.5. Графики напряжений.
4.5.6. Теоретические коэффициенты концентрации напряжений:
ασ1 = σmax1 / σном          ασ2 = σmax2 / σном
4.5.7. Выводы

Работу принял_________
“____”__________200 г.

Примечание: в выводах необходимо отметить следующее:
       как распределяются напряжения в ослабленном и неослабленном сечениях полосы;
       увеличивает или уменьшает прочность детали наличие концентратора напряжений;
       можно ли рассчитывать на прочность детали без учета концентрации напряжений.

4.6. Контрольные вопросы
  1. Как определить нормальное напряжение в неослабленном сечении полосы при растяжении?
  2. Что такое концентратор напряжений (примеры) и концентрация напряжений?
  3. Как распределяются нормальные напряжения в неослабленном сечении полосы при растяжении?
  4. Что такое номинальное напряжение?
  5. Как распределяются нормальные напряжения в ослабленном сечении полосы (в зоне концентрации)?
  6. Что такое теоретический коэффициент концентрации напряжений?
  7. Увеличивает или уменьшает прочность детали наличие концентраторов напряжений?