Лабораторная работа № 2
Определение модуля упругости и коэффициента Пуассона стали при растяженииЦель работы: экспериментальное определение модуля упругости и коэффициента Пуассона при растяжении.
Абсолютное удлинение стержня при растяжении – сжатии (рис. 2.1) в пределах упругих деформаций определяется по формуле:
Δl = (P · l) / (E · F), (2.1)
где Р – продольная (нормальная) сила;l – расчетная длина образца;
Е – модуль продольной упругости (модуль упругости при растяжении);
F – площадь поперечного сечения образца.
Из формулы (2.1) можно найти величину модуля упругости, определив опытным путем абсолютное удлинение образца Δl:
E = (P · l) / (Δl · F), (2.2)
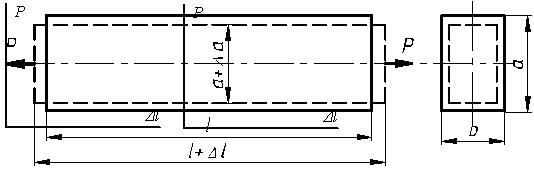
Рис.2.1
Следовательно, первая часть лабораторной работы заключается в определении абсолютного удлинения образца Δl на некоторой расчетной длине l.
Коэффициентом Пуассона называется абсолютная величина отношения относительной поперечной деформации ε' = Δa / a к относительной продольной деформации ε = Δl / l (рис. 2.1). Следовательно, если определить одновременно продольную и поперечную деформации образца, то можно вычислить величину коэффициента Пуассона:
μ = |ε' / ε|, (2.2)
Модуль упругости Е и коэффициент Пуассона μ характеризуют упругие свойства материала и определяются экспериментально. Для различных материалов коэффициент Пуассона изменяется от нуля (для пробки) до величины, близкой к 0,5 (для резины и парафина).
Для стали модуль упругости Е принимает значения в пределах (1,8 - 2,2) · 105 МПа, коэффициент Пуассона μ - в пределах (0,25 - 0,33).
2.2. Лабораторная работа № 2а
Определение модуля упругости и коэффициента Пуассона при растяжении с помощью механических тензометров2.2.1. Описание установки тензометров
Величина абсолютного удлинения и сужения образца (рис. 2.2) определяются при помощи рычажных тензометров Гугенбергера. Растяжение образца производится при помощи испытательной машины ИМ-4Р.
Чтобы исключить влияние неравномерного растяжения образца в случае неточной его установки в захватах машины, на образце закрепляют по два тензометра (по одному с каждой стороны), как показано на рис. 2.2. При этом тензометры 1 и 2 измеряют деформации в продольном направлении, а 3 и 4 – в поперечном направлении.
Величину модуля упругости вычисляют по формуле (2.2), а коэффициента Пуассона - по формуле (2.3).
- Убедиться, что рычажные тензометры сняты с предохранителей.
- Нагрузить образец предварительной нагрузкой Р0 = 500 кг (5 кН).
- Снять показания с тензометров и записать в журнал наблюдений (табл. 2.1).
- Нагрузить образец нагрузкой Р = 2000 кг (20 кН).
- Снять показания с тензометров и записать в журнал наблюдений (табл. 2.1).
Испытания проводятся три раза, затем находятся разности отсчетов по каждому испытанию и средняя разность отсчетов для всех испытаний по каждому тензометру.
Обработка результатов проводится в последовательности, представленной в таблице 2.2.
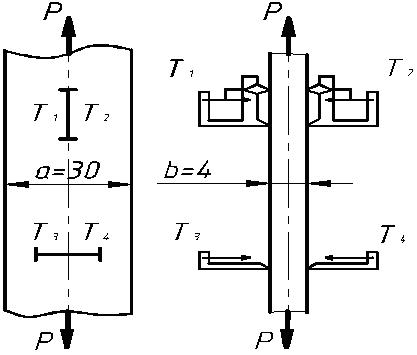
Рис.2.2
2.3. Образец отчета
Лабораторная работа №2-а
Определение модуля упругости и коэффициента Пуассона
с помощью механических тензометров
2.3.2. Схема испытательной установки (рис. 2.2)
2.3.3. Результаты испытаний
Таблица 2.1
| № испыт | Нагрузка Р,кг (кН) |
Продольные деформации | Поперечные деформации | ||||||
| T1 | T2 | T3 | T4 | ||||||
| отсчет n, (дел) |
раз- ность отсче- тов Δn, (дел) |
отсчет n, (дел) |
раз- ность отсче- тов Δn, (дел) |
отсчет n, (дел) |
раз- ность отсче- тов Δn, (дел) |
отсчет n, (дел) |
раз- ность отсче- тов Δn, (дел) |
||
| 1 | 500 (5) | ||||||||
| 2000 (20) | |||||||||
| 2 | 500 (5) | ||||||||
| 2000 (20) | |||||||||
| 3 | 500 (5) | ||||||||
| 2000 (20) | |||||||||
2.3.4. Обработка результатов испытаний
Таблица 2.2
| Расчетная формула | Тензометры | ||||
| T1 | T2 | T3 | T4 | ||
| Средняя разность (дел) | Δn = (Δn1 + Δn2 + Δn3) / 3 | ||||
| Абсолютное удлинение или укорочение (мм) на ступень нагружения ΔP=1500 кг (15 кН) | Δli = Δni · k = Δni · 10-3 | ||||
| Среднее абсолютное удлинение (укорочение) (мм) | Δlcp = (Δl1 + Δl2) / 2 | --- | |||
| Δlcp = (Δl3 + Δl4) / 2 | --- | ||||
| Относительная продольная (поперечная) деформация | ε = Δlcp / S | --- | |||
| ε' = Δl'cp / S | --- | ||||
| Коэффициент Пуассона | μ = |ε' / ε| | ||||
| Модуль упругости (кг/см2) (МПа) | E = ΔP / F · 1 / ε | ||||
Здесь: k = 10-3 – цена деления тензометра;
ΔP = P - P0 = 1500кг (15 кН) – ступень нагружения;
ε – относительная продольная деформация;
ε' – относительная поперечная деформация;
S = 20 мм – база тензометра;
F = a · b = 3 · 0.4 = 1.2 см2 = 1.2 · 10-4м2- площадь поперечного сечения образца.
2.3.5. Выводы:
Примечание: в выводах необходимо отметить, находятся ли полученные экспериментальным путем величины модуля упругости и коэффициента Пуассона в пределах табличных данных или нет.