Объемные свойства

Подавляющее большинство пищевых материалов относится к капиллярно - пористым телам. Первая аксиома реологии, утверждающая, что "под действием  всестороннего равномерного давления все материалы являются упругими", для простых пищевых материалов экспериментально не подтверждается.

При сжатии в замкнутом объеме таких пищевых масс, как хлебопекарное или макаронное тесто, пролиновые массы, мясной фарш, наблюдались остаточные деформации и рассасывание напряжений при сохранении постоянства объема.

Появление остаточных деформаций можно объяснить удалением защемленного воздуха и локальными пластическими деформациями материала вблизи полостей, образуемых порами. Локальные пластические деформации не восстанавливаются при снижении давления. Суммарный эффект многих таких микродеформации становится заметным  в макрообъеме.

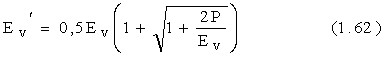
Теоретически установлено, что "кажущийся объемный модуль" Еv' определяется зависимостью:

где  Р – давление;
Еv - объемный модуль.
Из этой зависимости видно, что с увеличением давления кажущийся объемный модуль увеличивается.
В замкнутом  пространстве при фиксированном положении поршня наблюдается падение давления и рассасывание напряжения.

Ползучесть

Как мы уже кратко знакомились, под ползучестью понимается постепенное нарастание во времени деформации при постоянных напряжениях.

Явление ползучести наблюдается для многих материалов: для металлов оно характерно при повышенных температурах, а для материалов органического происхождения заметно проявляется и при нормальных температурах. Изучение ползучести пищевых материалов затрудняется тем, что характеристики их не стабильны, они зависят от очень многих факторов, кроме температуры t0 и влажности W, от способа приготовления материалов; соотношения свойств компонентов, входящих в материал;  времени  выдержки t между получением продукта и временем испытаний.

Это объясняется химико-биологическими процессами,  протекающими в сырье, меняющими его свойства.
Для металлов  изучение  ползучести важно при расчете на длительную прочность элементов конструкции. Для пищевых  материалов процессы ползучести, возникающие при прессовании и формовании, протекают во много раз быстрее, иногда измеряются часами и даже минутами, что приводит  к необходимости считаться с изменением технологических свойств сырья в процессе его обработки.

Кривые ползучести материалов, получаемые в процессе их испытаний, представляют номограммами в зависимости от величины прилагаемой нагрузки (см. рис.1.6).

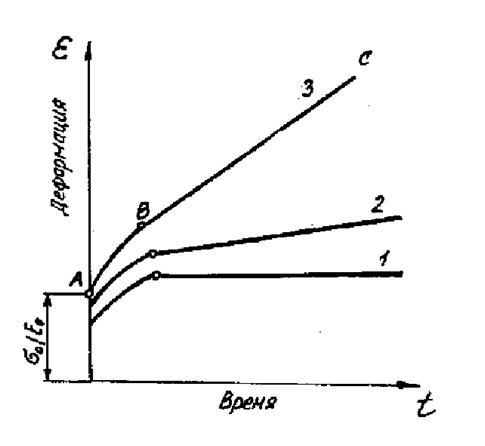
Рис. 1.6. Кривые ползучести.
1 - при малых нагрузках;
2 - при средних нагрузках;
3 - при больших нагрузках;
АВ – переходный процесс неустановившейся ползучести.

При малых нагрузках явления ползучести постепенно затухают, что является следствием релаксации и о чем будет сказано ниже. При больших нагрузках ползучесть может развиваться до разрушения.

Скорость деформации  V0 определяется тангенсом угла наклона к оси времени t касательной к кривой "деформация-время". При быстром наложении нагрузки, вызывающей напряжение s0, возникает упругая мгновенная деформация, равная s0/E0, где Е0 - мгновенный мо­дуль упругости, участок АВ - период неустановившейся ползучести (затухающей), участок ВС где скорость деформации величина постоянная – участок установившейся ползучести.

Предельное напряжение sп, при котором скорость деформации стремиться к нулю, а деформация - к некоторому конечному значению, emax называется пределом ползучести или пределом длительной  прочности. Если  действующие  напряжения  превышают  предел длительной прочности, то развивается явление незатухающей ползучести, в результате которых материал разрушается.

Процесс ползучести представляет собой наложение двух видов течения (первое течение - с убывающей скоростью, второе – упругое течение с постоянной скоростью).

Деформация ползучести eр = e  - e0 (где e - полная деформация, а e0 - упругая составляющая), как функция времени t может быть выражена экспериментальной зависимостью:


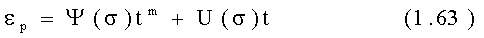
y(s) и U(s) - функции напряжения, определяемые экс­периментально


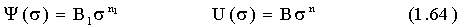
В1, В, n, n1 - экспериментальные коэффициенты, зависят от вида мате­риала n и n1< 1.
Таким образом, кривые ползучести представляют линейную деформацию e функцией напряжения s и времени t.

Кинетика деформации

Явление течения или кинетика деформации тесно связаны с явлением ползучести.

Если к образцу приложено напряжение больше предела текучести s > sт или  t > tт, то развитие деформации происходит следующим образом, представленным на рис.1.7.

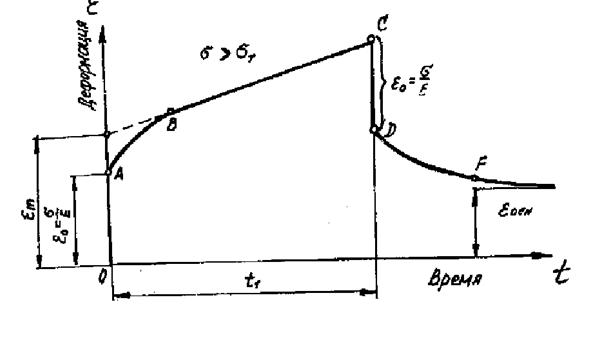
Рис.1.7. Кривая кинетики деформации:
OA – участок упругой деформации;
АВ – участок упругого последействия;
ВС – участок установившегося процесса необратимого пластического течения;
СD – восстановление упругой деформации;
DF – восстановление упругого последействия;
e0   - упругая деформация в момент нагружения;
em  - общая составляющая упругой деформации за время t1;
eост – конечное значение остаточной деформации после восстановления упругой деформации;
ti    - время выдержки под нагрузкой. 

При мгновенном приложении напряжения s возникает упругая деформация e0 = s/Е, где Е является мгновенным модулем упругой  деформации. Дальше развитие деформации идет по кривой АВ.  Криволинейность этого участка можно объяснить явлением упругого последействия, когда одновременно развивается упругая и пластическая деформации. Через определенное время устанавливается прямолинейная зависимость (участок ВС), отвечающая установившемуся стационарному процессу необратимого пластического течения, при постоянном значении упругой деформации. На участке ВС деформация нарастает с постоянной скоростью, которая характеризуется тангенсом угла наклона прямой ВС. Скорость течения gТ’ пропорциональна напряжению (s – sТ) и обратно пропорциональна пластической вязкости hпл. Для этого участка справедливо равенство:

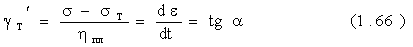
При sТ = 0 пластическая вязкость будет ньютоновской вязкостью, и будет наблюдаться вязкое течение. Продолжая прямую ВС до пересечения с осью ординат, получим отрезок Еm соответствующий упругой части деформации участка ОА и криволинейного участка АВ. При времени t = t1 напряжение снимается, участок CD по величине равный ОА, при этом исчезает часть упругой деформации e0 = s/Е. С увеличением времени t кривая DF будет  асимптотиче­ски приближаться к  конечному  значению  деформации, которая является остаточной – eост.

Приведенная картина развития деформации при действии постоянного напряжения не является справедливой для всех пищевых материалов. Так при приложении мгновенного напряжения, кроме мгновенной упругой деформации, может появляться мгновенная пластическая деформация а также может отсутствовать скачок при снятии нагрузки.

Виды жидкостей. Неньютоновские жидкости

Жидкости, у  которых вязкость при заданных температуре и давлении зависит от скорости деформации и от ее предыстории, относятся к неньютоновским (аномальным).
Оствальд И. объяснил аномальное поведение жидкости разжижением структуры и ввел новый термин "структурная вязкость".

Нелинейность течения, обусловленная изменением вязкости, может быть вызвана различными  причинами. Зависимость вязкости от скорости сдвига, характерна для дисперсных систем. Дисперсные многофазные системы можно представить в виде непрерывной среды (дисперсной среды), в которой распределено раздробленное вещество (дисперсная фаза). Взвешенные частицы дисперсной фазы могут представлять собой частицы сложной формы различно ориентированные в дисперсной среде. Если частицы имеют удлиненную форму, то при течении они будут поворачиваться и ориентироваться вдоль оси течения. Такая ориентация влечет за собой изменение вязкости. Ориентацию частиц нарушает диффузия из-за броуновского движения, влияние которой увеличивается с повышением температуры. При дисперсной фазе в виде жестких шариков, взвешенных в простой ньютоновской жидкости, с изменением скорости сдвига вязкость не меняется.
Изменение вязкости может происходить за счет упругой деформации частиц и их вращения.  Наибольшее растяжение частиц получается при наклоне их главной оси под углом 45 градусов к направлению сдвига, т.к. при простом сдвиге максимальные напряжения растяжения и сжатия наклонены под углом 45 градусов к направлению сдвига. При вращении частиц происходит разгружение и нагружение частиц, эти колебания передаются жидкости, и количество энергии дисперсии возрастает. В этом случае при увеличении скорости сдвига вязкость повышается.

Если растяжение частиц велико, а сами частицы имеют небольшую прочность, то может произойти их разрушение, сопровождающееся укорочением. Укорочение частиц приближает их к шарообразной форме, что ведет к понижению вязкости. Частично, при определенных усло­виях, частицы могут  восстанавливаться, поэтому кривая консистентности, полученная при увеличении величины сдвига, будет отличаться от кривой консистенции, полученной при уменьшении величины сдвига, т.е. будет получаться петля гистерезиса.
Частицы дисперсной фазы могут быть в виде нежестких или эластичных нитей. Натяжение нитей вызывает распределение их. Такое явление ведет к уменьшению взаимодействия частиц с потоком жидкости и понижению вязкости.

В дисперсных системах, обладающих пространственной структурой, нелинейность может получаться вследствие разрушения структуры. Если обрывки частиц в процессе течения соприкасаются друг с другом, то они восстанавливаются. Для всякой скорости сдвига существует динамическое равновесие между скоростью распада и скоростью восстановления. Если построить консистентные кривые то при увеличении скорости сдвига, а затем при уменьшении получается петля гистерезиса. Описанное явление называется тиксотропией.
У. Уилкинсон предложил реальные жидкости с нелинейной кривой – неньютоновсие жидкости течения разбить на следующие три типа.

• Системы, для которых скорость сдвига в каждой точке представляет некоторую функцию только напряжения в той же точке.
• Системы, в которых связь между напряжением и скоростью сдвига зависит от времени действия напряжения или от предыстории жидкости.
• Системы,  обладающие свойствами, как твердого тела, так и жидкости, и частично  проявляющие упругое восстановление формы после снятия напряжения (вязкоупругие жидкости).

9.1. Система неньютоновских жидкостей первого типа

К системе первого типа (см. рис. 18) относятся:
а) бингамовские пластические жидкости (бингамовские пластики);
б) псевдопластические жидкости (псевдопластики);
в) дилатантные жидкости.
Все они описываются реологическим уравнением вида:


9.1.1. Бингамовские пластики - это тела, у которых в покое имеется пространственная структура, которая сопротивляется напряжению ниже предельного напряжения сдвига q.  При напряжениях больше q структура разрушается, и тела ведут  себя  как ньютоновская жидкость при напряжениях сдвига tн = t – q. Как только напряжения сдвига становятся меньше q, структура снова восстанавливается.

9.1.2. Псевдопластические жидкости - это тела, которые не имеют предела текучести, и эффективная вязкость hэф с ростом скорости сдвига постоянно понижается. Понижение  вязкости можно объяснить ориентацией асимметрических частиц своими главными осями вдоль направления потока.
По Оствальду И. и Рейнеру М.

где k - мера консистенции жидкости: чем выше вязкость, тем больше k;
n - коэффициент меньше единицы: для ньютоновской жидкости равен единице;
g - величина сдвига.

9.1.3. Дилатантные жидкости - тоже не имеют предела текучести, но в отличие от псевдопластиков у них эффективная вязкость повышается с увеличением скорости сдвига. Для описания их поведения можно применить степенной закон по зависимости (1.68), но показатель степени n будет больше единицы (закон Оствальда-Рейнера). Кривые течения, характерные для этих жидкостей приводятся на рис.1.8,  где для сравнения приведены графики для ньютоновской жидкости.

Рис.1.8. Кривые течения (а) и зависимость вязкости от скорости сдвига (б):
1- бингамовская жидкость; 2 - псевдопластическая жидкость; 3 - ньютоновская жидкость; 4 - дилатантная жидкость.

9.2. Система неньютоновских жидкостей второго типа

К системе второго типа относятся жидкости, реологические характеристики которых зависят от времени. К ним относятся:
а) типсотропные;
б) реопектические жидкости.

9.2.1. Типсотропные жидкости - это такие материалы, консистентные кривые которых зависят от продолжительности и скорости сдвига (см. рис.1.9), и эти жидкости, как уже было сказано, обладают способностью образовывать петлю гистерезиса.

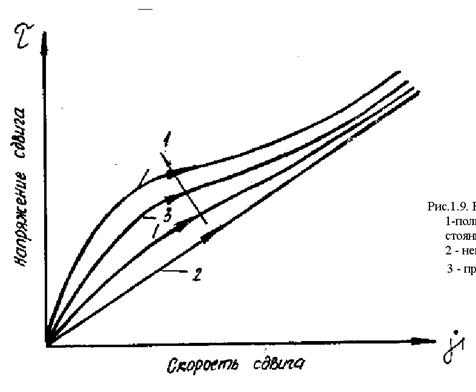
Рис.1.9. Кривые течения типсотропных материалов:
1 - полное восстановление структуры при длительном стоянии; 2 - непосредственно после длительного сдвига; 3 - промежуточное состояние.

9.2.2. Реопектические жидкости - характеризуются  постепенным  структурообразованием и повышением вязкости при сдвиге. Такие материалы практически существуют в природе, но их обнаружено мало.

9.3. Третья группа неньютоновских жидкостей.

Это вязко-упругие, проявляющие как упругое восстановление формы, так и вязкое течение, - типичным примером является максвеловская жидкость. Из пищевых масс таким свойством обладает дрожжевое тесто и др.

9.4. Аналитическое выражение свойств неньютоновских жидкостей

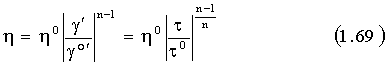
Для многих пищевых материалов можно рекомендовать степенной закон, который описывает изменение вязкости псевдопластических и дилатантных жидкостей:

где     g0' и t0 - скорость сдвига и напряжение сдвига в произвольно выбранном состоянии;
h0  - вязкость неньютоновской жидкости в произвольно выбранном состоянии.
Параметр n является индексом течения. Когда индекс течения n равен единице, то степенной  закон сводится к закону Ньютона (рис.1.8 а,  кривая 3). При n<1 (рис.1.8 а, кривая 2) вязкость жидкости уменьшается с увеличением скорости или напряжения сдвига, т.е. в этом случае степенной закон описывает поведение псевдопластической  жидкости; если  n>1 (рис.1.8 а, кривая 4), то поведение дилатантной системы. Чем больше n отличается от единицы, тем больше жидкости отличаются от ньютоновской.

Если учесть,  что t = hg’, то можно описать степенное уравнение в виде:

Если взять знак t таким же, как знак g’ и если принять g0' = 1 и g’ положительным числом, то, логарифмируя уравнение, получим:

       

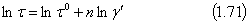
Из этого можно сделать вывод, что для жидкостей, подчиняющихся степенному закону, график зависимости ln t от g' является прямая линия.

10. Методы и приборы для определения  реологическиххарактеристик пищевых масс

Определение структурно-механических свойств пищевых масс в лабораторных условиях относится к вопросам реологии – экспериментальной реологии. Необходимо определять параметры обрабатываемого сырья для повседневного технологического контроля производства и расчета параметров проектируемых рабочих органов. Существенные отклонения от принятых норм могут сказаться не только на качестве готовых изделий, но и на проведении отдельных процессов. При наблюдениях на практике диапазонов изменения скорости  сдвига, температуры и давления вязкость пищевых материалов варьируется в очень широких пределах. Поэтому основной задачей экспериментальных работ является определение изменений свойств материала, проходящих под влиянием тех или иных факторов.

Наиболее простой метод изучения структурно-механических свойств пищевых материалов заключается в построении кривых кинетики деформации. По этим кривым можно найти независимые друг от друга деформационные характеристики материала:
- модуль мгновенной упругости и упругого последействия E и En;
- релаксационную (течения) вязкость h;
- вязкость упругого последействия hn;
- предел упругости t;
- предел текучести tт, или предельное напряжение сдвига q;
- предел прочности tр, (tр не постоянен и зависит от механического режима деформирования).
Получение таких характеристик возможно в процессе изучения пищевых масс, т.е. при изучении процесса их течения под действием напряжения.
Наиболее важным реологическим показателем свойств материала является зависимость скорости деформации от напряжения.
Исследование упругопластических свойств дисперсных  пищевых систем по кривым кинетики деформации в основном проводились методом тангенциально-смещаемой пластины на приборе Вейлера-Ребиндера или на  ротационном  вискозиметре Воларовича. Для неньютоновских жидкостей реологические свойства, характеризующиеся кривой зависимости скорости деформации от напряжения, называются кривыми течения или реограммами.
Реологические методы исследования и приборы, условно, в зависимости от назначения и конструкции, делятся на: интегральные - дающие возможность определить суммарный эффект течения; дифференциальные - позволяющие наблюдать непосредственно деформацию во времени в каждой точке дисперсной системы при ее течении; с однородным полем напряжений и деформаций; с неоднородным полем.

10.1. Интегральные приборы

Интегральные приборы с однородным полем напряжения, включают ротационные вискозиметры и приборы с поступательным перемещением рабочего органа.

10.1.1. Ротационные вискозиметры с однородным  полем напряжений в соответствии с формой ротора делятся на:
а) цилиндрические;
б) конус-плоскость;
в) дисковые;
г) биоконические;
Для цилиндрических и биоконических приборов скорость сдвига принимается одинаковой во всех точках деформируемого материала.
Что позволяет при изменении показаний скорости сдвига выяснить ее зависимость от величины напряжения, то есть получить кривые течения.
Существенным преимуществом ротационных вискозиметров является то, что свойства масс определяется  после  предварительного напряжения и механической обработки, то есть, как бы в условиях, в которых материал находится в перерабатывающей машине. Эти приборы используются для изучения свойств мучного теста, мясного фарша, кондитерских масс, помады и др.

А) Цилиндрические вискозиметры. Наибольшее распространение получил вискозиметр конструкции Воларовича РВ-8 (см. рис. 1.10). Малый зазор между ротором и стаканом делает течение материала близким к простому сдвигу. Простая методика наблюдения и обработки опытных данных. Больше подходит для веществ с большой вязкостью.

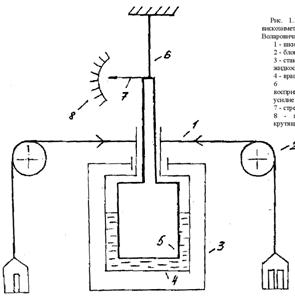
   Рис. 1.10. Схема ротационного вискозиметра РВ-8 системы Воларовича:
1 - шкив; 2 - блок; 3 - стакан для термостатирующей жидкости; 4 - вращающийся стакан;
6 - упругая нить воспринимающая увеличенное  усилие закручивания; 7 - стрелка; 8 - шкала для определения крутящих моментов.

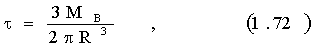
На вискозиметре получают значения крутящих моментов М в зависимости от угловой скорости w, напряжения сдвига t и скорость деформации g’, которые находятся по формулам:


где  R - радиус подвижного цилиндра;
D  - зазор между внешним и внутренним цилиндрами.

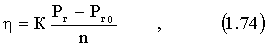
Вязкость h и предельное напряжение сдвига tт определяется по формуле:

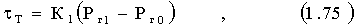
где  Рг - груз, вращающий внутренний цилиндр вискозиметра;
Рг1- максимальный груз, при котором начинается вращение цилиндра;
Рг2- нагрузка идущая на преодоления трения в подшипниках;
n - число оборотов внутреннего ротора вискозиметра;
К и К1 - константы вискозиметра, зависящие от его геометрических размеров и глубины, на которую загружается исследуемая масса.

Б) Вискозиметр конус-плоскость - сравнительно новый тип вискозиметра (см. рис. 1.11). Крутящий момент, прикладываемый к конусу подвешенными грузами, уравновешивается вращением плиты на такой скорости, которая обеспечивает отсутствие вращения конуса.

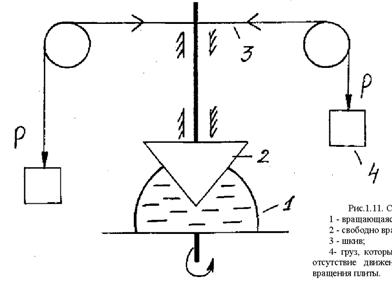
Рис.1.11. Схема вискозиметра конус - плоскость:
1 - вращающаяся с переменной скоростью плита; 2 - свободно вращающийся конус;
3 - шкив; 4- груз, который подбирается так чтобы обеспечить отсутствие движения конуса
при заданной скорости вращения плиты.

10.1.2. Приборы с поступательным перемещением - применяются при сравнительно малых скоростях и величинах деформации. Конструкция подвижного элемента может быть выполнена в виде:
- Рифленого цилиндра, перемещаемого вдоль оси, когда снаружи находится материал;
- Горизонтальной плоскости, сдвигаемой тангенциально на кубике из испытуемого материала (будет подробно рассмотрен при изучении трибометров);
- Перемещаемой вертикальной плоскости вытаскиваемой из сосуда с исследуемой массой.
Эти приборы также относятся к приборам с плоскопараллельным зазором. В них зазор может быть расположен вертикально, горизонтально и наклонно.

10.1.3. Прибор с вертикальным расположением пластины - предложен С.А. Вейлером и П.А.  Ребиндером. Схема его  конструкции приведена на рис.1.12.

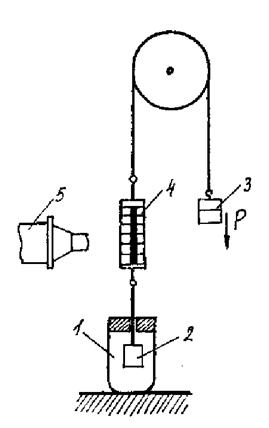
Рис.1.12. Схема прибора Вайлера-Ребиндера:
1 - кювета с исследуемым материалом; 2 - перемещаемая пластина; 3 – груз, приводимый в  движение пластину; 4 - микрошкала; 5 - микроскоп.

Напряжение сдвига t вычисляется по величине нагрузки P к боковой поверхности пластины F:

Предельное напряжение сдвига q (tт), характеризующее прочность структуры исследуемого материала определяется по наибольшей  нагрузке Pmax

Метод тангенциального смещения пластины позволяет находить не только ?, но и модуль упругости Е, эффективную вязкость hэф, изучать процесс релаксации, а также снимать полные деформационные кривые g’ = f(t) при разных скоростях деформации. Приборы, основанные на этом методе, обладают большой чувствительностью и применимы для исследования свойств от слабо структурированных золей и суспензий до твердообразных систем с высокопрочной структурой.

10.1.4. Интегральные приборы с неоднородным полем напряжений – включают в себя: а) капиллярные вискозиметры; б) конические пластометры; в) шариковые вискозиметры; г) приборы, основанные на методе колебаний.

А) Капиллярные  вискозиметры  предназначены  для исследования веществ с малой вязкостью,  хотя в некоторых случаях их применяют и для изучения веществ с высокой вязкостью.
На капиллярных и ротационнных вискозиметрах экспериментально осуществляются принципиально различные типы течения. В капиллярных вискозиметрах измерения проводят в существенно неоднородном поле скоростей деформаций и напряжений, причем время пребывания материала в капиллярах является ограниченным. В ротационных же приборах напротив, течение происходит в поле напряжений высокой степени однородности. Кроме этого капиллярность вискозиметра имеют еще ценный ряд преимуществ: в капилляре непрерывно подвергается сдвигу вновь поступающая жидкость, и тепловыделения уносятся с материалом, тогда как в ротационном вискозиметре один и тот же испытуемый  материал  находится в зазоре вискозиметра в течение всего опыта.
Капиллярные вискозиметры наиболее просты по устройству (см. рис.1.13). Метод определения основан на установлении зависимости между напряжением и скоростью сдвига косвенным способом – по измерении перепада давления и расходу жидкости.

 
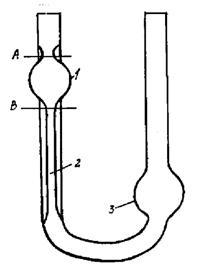
Рис. 1.13. Капиллярный вискозиметр:
1 - емкость для измерения количества протекающей через капилляр жидкости; 2 - капилляр; 3 - емкость для сбора жидкости.

Как уже  было упомянуто выше, капиллярные вискозиметры (см. рис.1.13) представляют собой U - образную трубку, в одно из колец которой помещен капилляр. Переливание жидкости из одного колена в другое происходит за счет гидростатического давления. Капилляр располагается вертикально.  Для значительно вязких жидкостей Воларовичем М.П. и Кулаковым Н.Н. предложен вискозиметр с горизонтальным капилляром; в нем исключается необходимость поправки на гидростатическое давление столба исследуемого материала, что нужно делать обязательно при вертикальном капилляре.

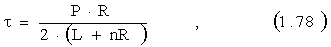
В опытах на капиллярных вискозиметрах оперируют зависимостью расхода Q от перепада давлений Р. Напряжение сдвига t (действующее на стенки капилляра) рассчитывают по формуле:

где R - радиус капилляра;
Р – перепад давления;
L - длина капилляра;
n - поправка, учитывающая концевые эффекты.
Скорость сдвига  (на стенке капилляра) рассчитывается по формуле:


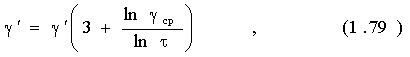
где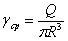      
Q - объемный расход.

Такие вискозиметры применялись для определения вязкости бульоны и топленого жира, крови, подсолнечных, соевых, миндальных и арахисового масел, кондитерского жира, крахмала кукурузы, то есть для тех веществ, которые имеют небольшую вязкость.

Б) Конические пластомеры просты, но при их использовании без особых затруднений, находится важнейшая реологическая характеристика материала - предельное напряжение сдвига q. Схема конструкции прибора, предложенного Г.А. Ребиндером и Н.А. Семененко приведена на рис. 1.14.

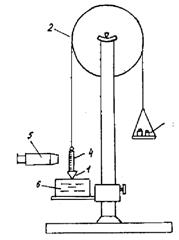
Рис. 1.14.  Схема конического пластометра Ребиндера -  Семененко:
1 - конус; 2 - блок; 3 - груз; 4 - шкала; 5 - микроскоп; 6 - образец.

Величина предельного напряжения сдвига q (tт) вычисляется по максимальному погружению конуса hmax в исследуемый материал

 где Pг - нагрузка, действующая на конус, вес груза;
Ka - константа конуса, зависящая от угла при вершине;

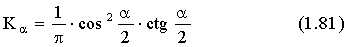
hmax - величина погружения конуса в исследуемый материал.

где a - угол при вершине конуса.

Исследуемая масса помещается в сосуд на подъемный  столик, вершина конуса приводится в соприкосновение с поверхностью массы. Конус нагружается гирями и с помощью индикатора определяется глубина погружения конуса до полной его остановки.
На данном приборе проводились опыты с косметическими и кондитерскими кремами и конфетными массами.

В) Приборы, основанные на методе падения шарика в трубе, заполненной исследуемым продуктом, используются для тех же материалов, что и капиллярные вискозометры. Заслуживает внимания вискозиметр Гиплера. В нем жидкость помещается в наклонную трубку, в которой перемещается шарик. Между трубкой и шариком остается небольшая щель. Исследуемые характеристики определяются по времени падения шарика. Недостатком данного прибора является невозможность воспроизведения результатов в двух последовательных опытах  из-за разрушения структуры исследуемого вещества.

Г) Приборы, основанные на методе колебаний, как механических, так и электрических, к этим приборам можно также отнести приборы с одномерным растяжением материала. Эти приборы применяются, когда материал обладает высокой вязкостью и значительной неоднородностью структуры.

10.1.5. Приборы для определения деформации растяжения, сжатия – используются для оценки свойств вязко-текучих материалов. Для исследования деформации растяжения хлебопекарного теста, используют экстенсографы, в которых цилиндр из теста закрепляют горизонтально и деформируют его силой, направленной вертикально и приложенной в середине цилиндра перпендикулярно его продольной оси. На таком приборе определяют мгновенный модуль упругости Е0, влияния продолжительность замеса и отлежки, а также влияние обработки теста на его пластические свойства.
Схема экстенсографа  фирмы  "Брабендер"  приведена  на рис.1.15.
Тесто замешивается на месилке до определенной концепции, делится на куски весом 150 г. Затем из них с помощью валиков формируют цилиндры, которые в дальнейшем подвергают отлежки в течение 45 минут в специальном сосуде. Для проведения опыта тестовой цилиндр помещают в держатель аппарата, который от перемещения удерживается скобами. Рычаг, приводимый в движение двигателем, производит нагружение с постоянной скоростью вертикально вниз перпендикулярно оси тестового цилиндра. Усилия, возникающие  при растяжении теста, через систему рычагов передаются к пишущему устройству. На бумаге вырисовывается кривая растяжения теста - экстенсограмма.

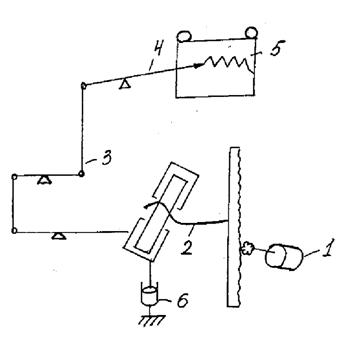
     Рис. 1.15. Схема экстенсографа фирмы "Брабендер":
1 - приводной двигатель; 2 - рычаг нагружения; 3 – система рычагов; 4 - пишущий элемент; 5 - лентопротяжное устройство; 6 - масляный амортизатор для смягчения колебаний рычажной системы  в момент разрыва тестового шнура.

Приборы для  измерения деформации при сжатии применяются для определения упругопластических свойств различных веществ (например, теста). На рис.1.16 приведена схема прибора Б.А. Николаева и А.С. Шпингельгляса для измерения деформации одноосного сжатия между параллельными плоскостями.

Рис. 1.16. Схема прибора для определения деформаций сжатия Николаева–Шпингельгляса:
1 - станина; 2 - столик для образца; 3 - верхний диск; 4 - столик для грузов; 5 - рейка зубчатая; 6 - стрелка; 7-шкала; 8 – эксцентрик, регулирующий контакт испытуемого материала с дисками.

Работа на приборе производится следующим образом: на столике 2 укладывается образец и измеряют его первоначальную высоту, затем  быстро поднимают столик 2 и нагружают груз 4. Определяют величину мгновенной деформации по шкале 7, а также изменения ее, отсчитывая время по секундомеру. На данном приборе можно определить мгновенно упругую деформацию e0, модуль упругости Е0, а также вязкость h и предельное напряжение сдвига материала q.
Для исследования физических свойств при  постоянно  изменяющейся нагрузке образцов лапши при ее постоянном удлинении (релаксации напряжения) применяется прибор, схема которого приведена  на рис. 1.17.

             Рис. 1.17. Схема прибора для испытания на растяжение:
1 - зажимы; 2 - системы рычагов; 3 - скользящий груз; 4 - стрелка; 5 - шкала.

Нагрузка W, на образец менялась при помощи системы неравноплечных рычагов по отклонению отвеса W0. В результате опытов строились графики изменения нагрузки в зависимости от сопротивляемости образца, а также кривые изменения деформации образца во времени.

10.2. Дифференциальные методы измерений и приборы

Ротационные вискозиметры, у них на торце легко наблюдается распределение скоростей в массе испытуемого вещества. В таких приборах можно хорошо наблюдать границу между зонами пластической и упругой деформации.
Капиллярные вискозиметры, с их помощью можно наблюдать изменение скоростей течения материала в трубах.
Наблюдение с использованием дифференциальных методов и приборов требует специальной подготовки образцов и сложных методик. Поэтому при выборе метода исследования и приборов для определения реологических свойств какого-нибудь вещества, необходимо, прежде всего, учитывать условия, в которых оно находится в перерабатывающих машинах.