

Вязкость
Модель вязкой жидкости Ньютона предполагает, что сдвиговое напряжение ? прямо пропорционально скорости деформации t = hg’, о чем уже было сказано, а коэффициент пропорциональности h именуется вязкостью. Он имеет размерность напряжения, помноженного на время, и измеряется Н сек/м2 [1пз = 1дин сек/м2 = 0,1 Н сек/м2].
Отсюда следует, что если цилиндрический вал вращается в ванне, заполненной вязкой жидкостью, то, по исследованиям Стокса (английский физик XIX века), крутящий момент М, действующий на слой жидкости, будет пропорционален квадрату расстояния R2 от оси цилиндра.
4.1. Модель вязкого поведения жидкости
Для ньютоновской жидкости рассмотрим схему ламинарного течения жидкости в горизонтальной трубе - капилляре. При горизонтальном расположении трубы вес жидкости не имеет значения. Выделим цилиндр длиной l и радиусом r ; на длине l перепад давления будет DР (см. рис.1.4).
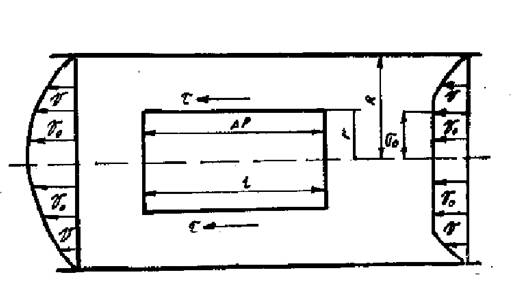
Рис.1.4. Схема течения жидкости в трубе:
V, V0 – скорость движения жидкости.
Условие равновесия выделенного объема представляется зависимостью:
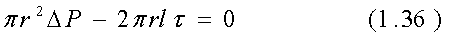
где t – касательное напряжение,
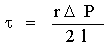
откуда
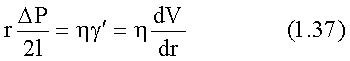
Из уравнения Ньютона
где V – скорость течения жидкости;
h – вязкость.
Интегрируя

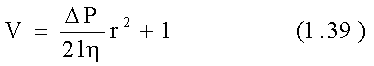
получим
(Знак минус упущен, он показывает, что течение противоположно возрастанию давления.)
Постоянную интегрирования находят из условия r = RV = 0, тогда:
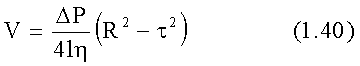
где R – радиус капилляра.

Распределение скорости будет параболическим. Расход Q может быть получен интегрированием уравнения:
где dF=2prdr - элемент площади.
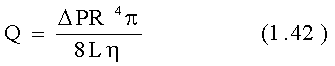
Это закон Пуазейля.
Для ламинарного течения жидкости Бингама - Шведова:

где hпл – вязкость пластично-вязкого тела Бингама – Шведова.
Представляя t = rDP/2L и g = dV/dr,
получим:
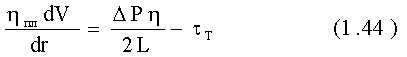
Интегрирование дает
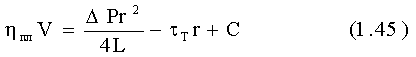
Постоянную С определяем из условия прилипания материала к стенке цилиндра при r=R, V=0
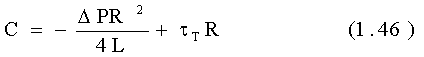
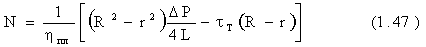
Отбрасывая знак минус, как и при выводе закона Пуазейля, получим

Из исходного уравнения видно, что при DPr0/2L = tт (производная скорости равна нулю), dV/dr = 0. Это указывает на то, что при r ? r0 есть движение с постоянной скоростью, но течение отсутствует, т.е. нет относительного смещения слоев. Это говорит о том, что около оси тело будет двигаться как жесткое, и, где t ? tт, при этом радиус жесткого ядра R0 определяется уравнением:
Скорость V0 жесткого цилиндра находится подстановкой r0 вместо r и tт = DPr0/2L
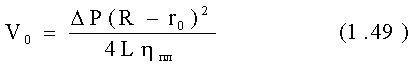
и распределением скорости по сечению трубы будет усеченная парабола.
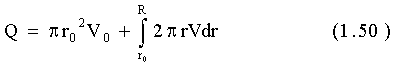
Расход Q может быть выяснен как сумма двух расходов; в центральной зоне со скоростью V0 и в остальной части сечения с переменной скоростью V расход равен:
после подстановки выражений V0, V, r и интегрирования, находим
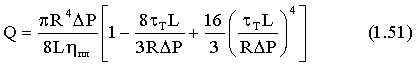
Это уравнение известно под названием уравнения Букингема - Рейнера.
4.2. Экспериментальное определение вязкости
Наука о количественной оценке вязкости материалов, как часть экспериментальной реологии (реометрии), называется вискозиметрия. Существует разнообразие методов и конструкций приборов обусловленная широким диапазоном измерений (10-5 у газов до 1012 Н?сек/м2 у ряда полимеров) и необходимостью их осуществления при низких и высоких температурах и давлениях.
Вязкость определяется различными способами и приборами. Приборы для определения вязкости называются вискозиметры. Они используются также для оценки и других консистентных переменных. Наиболее распространены: ротационные, основанные на законах внутрижидкостного трения; капиллярные, основанные на законе Пуазейля; с падающим шариком, основанные на законе Стокса; ультразвуковые основанные на затухании ультразвуковых колебаний в вязкой среде. Подробное описание способов применения и конструкции приборов для определения вязкости приведено в §10.
