Моделирование реологического поведения тел

Идеальные тела.  Это понятие условное, в природе таких нет, но они  приняты как отправной пункт при рассмотрении и описании поведения реальных материалов, составляющих те или иные комбинации свойств идеальных тел.

Известно три вида идеализированных материалов:
- идеально-упругое тело Гука;
- идеально-пластическое тело Сен-Венана;
- идеальная вязкая жидкость Ньютона.

Упругое тело является консервативной системой, т.е. энергия, затрачиваемая на деформацию,  накапливается в теле и может  быть возвращена при разгрузке.

Вязкая жидкость и пластическое тело  являются  диссипативными системами: механическая энергия, затраченная на работу преодоления внутреннего трения и на пластическую деформацию,  превращается в теплоту.

В упругом теле напряженное состояние связано с мгновенной деформацией, а в вязкой жидкости и пластических телах с  мгновенным состоянием  течения. В случае вязкого течения затрачиваемая механическая энергия зависит от  скорости  деформации, в случае пластического течения - не зависит.

3.1. Идеально-упругое тело Гука

Идеально-упругое тело Гука (см. табл.1.1 п.а) - это упругое тело, подчиняющееся закону Гука,  для одномерной задачи может быть описано уравнением:

где  s - нормальное напряжение;
E  - модуль упругости;
e - линейная деформация.

                                          Таблица 1.1.

                    
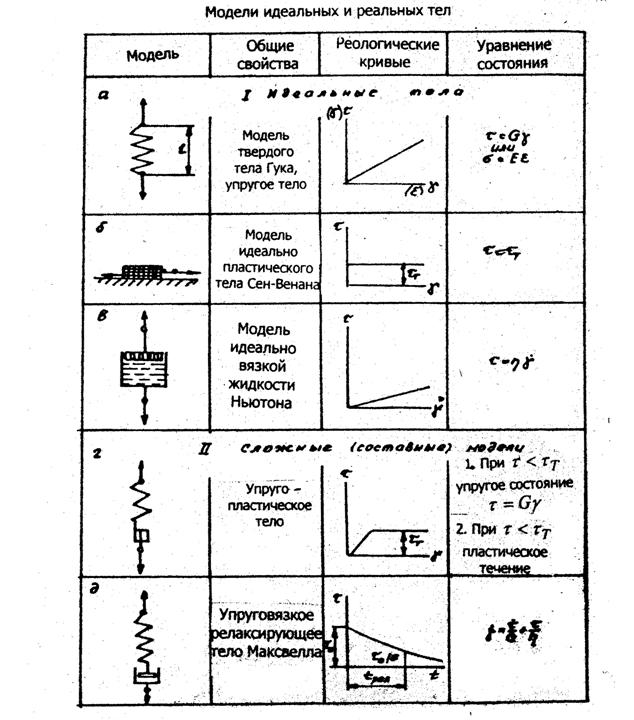
Деформация возрастает  непосредственно после приложения нагрузки, скорость распространения деформации мгновенна (реально во всех материалах - со скоростью распространения волн в среде). Если рассматривать деформацию  призмы,  находящейся  под  действием сдвигающего (касательного)  напряжения,  приложенного  к  верхней грани, то закон Гука принимает вид:

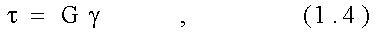
где  t - касательное напряжение;
G - модуль сдвига;
g - угол сдвига или градиент смещения.
Модуль сдвига G связан с модулем упругости  (растяжение-сжатие) Е зависимостью:


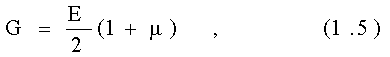
где m - коэффициент Пуассона.

Моделью идеального упругого тела Гука может служить спиральная пружина.

3.2. Идеально-пластическое тело Сен-Венана

Идеально-пластическое тело Сен-Венана (см. табл.1.1. п.б). Поведение его, под нагрузкой, следующее: до тех пор, пока величина приложенного к нему напряжения лежит ниже некоторого критического значения предельного напряжения сдвига sт (tт) (предела текучести), материал остается жестким; в тот момент, когда напряжение достигает предела текучести, начинается пластическое течение материала при постоянном напряжении (примером является пластилин).

Модель идеально пластического  тела  Сен-Венана  может  быть представлена в виде элемента, лежащего на плоскости, с постоянным по величине трением, не зависящем от нормальной силы. Статический и кинематический коэффициенты трения принимаются равными. Тело не начинает двигаться до тех пор, пока напряжение сдвига не превысит предельного напряжения сдвига. После этого элемент может двигаться с любой скоростью. Реологическое уравнение будет иметь вид:

где  t - касательные напряжения;
tт - касательные напряжения течения (предельное напряжение сдвига, предел текучести).

3.3. Идеальная вязкая жидкость Ньютона

Идеальная вязкая   жидкость   или   Ньютоновская    жидкость (см. табл.1.1, п.в) может быть представлена моделью в виде перфорированного поршня, перемещающегося в цилиндре с жидкостью. Модель характеризуется тем, что в ней напряжения пропорциональны скорости деформации, поэтому реологическое уравнение имеет вид:

где  h - коэффициент вязкости;
g’ - скорость сдвига.

3.4. Сложные или составные модели

Для моделирования реальных тел, обладающих всеми реологическими свойствами в неодинаковой степени, можно комбинировать моделями идеальных тел в различных сочетаниях. К составлению моделей нужно относится с осторожностью,  иначе попытка отразить все многообразие свойств приводит в весьма сложным и, поэтому неприемлемым, реологическим моделям. В некоторых случаях реологическая модель может удовлетворительно отражать свойства реальных тел только в определенных интервалах изменения температуры,  влажности, давления и других параметров. За пределами этих интервалов поведение реального тела вследствие изменения его свойств может сильно расходиться с составленной моделью.
Модели идеальных тел могут соединяться между собой параллельно или последовательно. При параллельном соединении нагрузка складывается из  нагрузок ветвей, а скорости удлинения элементов одинаковы. При последовательном соединении нагрузка  на  элементы одинакова, а величина перемещения складывается из перемещений составляющих элементов.

3.5. Упруго-пластическое тело

Упруго-пластическое тело (см. табл.1.1,п.г) получается при последовательном соединении упругого и пластического элементов.
При t < tт  имеет место упругое состояние, при котором t = Gg; при t = tт наступает состояние пластического тече­ния.

3.6. Упруго-вязкое релаксирующее тело Максвелла

Упруго-вязкое тело Максвелла (см. табл.1.1,п.д) представляет собой последовательное соединение моделей гуковского и ньютоновского тел.
Из условия, что суммарная деформация ? равна сумме деформаций упругого ?У и вязкого ?? элементов, с учетом зависимостей 1.4 и 1.7 имеем:

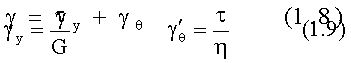
Дифференциальное уравнение данного тела:

Интегрируя это уравнение, получим его решение


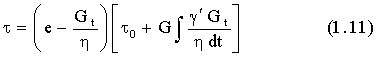
где t0 - напряжение в начальный момент времени (t=0).
Если мгновенно загрузить рассматриваемое тело и считать, что в момент t=0 приложено напряжение t0, то непосредственно после нагрузки тела вязкая деформация равна нулю и деформация  тела  равна полной упругой деформации:

Если после этого обеспечить неизменность во времени этой деформации, т.е. g = g0, то g = 0, тогда дифференцируемое уравнение при­мет вид:

Откуда, интегрируя, находим:

Отметим, что



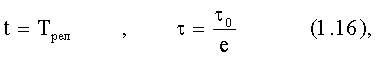
и         
определяется - Tрел период релаксации, как время, за которое напряжение упадет в е раз. При увеличении t напряжение t уменьшиться, при t тело переходит в ненапряженное состояние.

3.7. Тело Кельвина или Фойгта

Тело Кельвина или Фойгта (см. табл.1.1,п.е) получается при параллельном соединении упругого и вязкого элементов. В этом случае суммарное напряжение равно сумме напряжений ty и tВ, и де­формация упругого элемента равна деформации вязкого элемента

Учитывая, что ty = gG     и      tВ = hg'      получим:

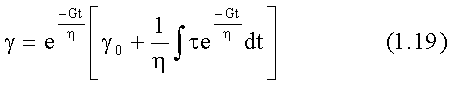
Интегрируя это уравнение, найдем общее решение:

где g0 - деформация в начальный момент времени (t=0).

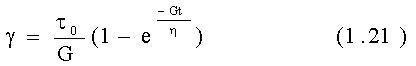
Рассмотрим случай, когда начальная деформация g0 = 0, а приложенное напряжение t0 постоянно, тогда уравнение примет вид:

Из исходного  уравнения следует,  что модель тела Кельвина-Фойгта для описания процесса релаксации не приемлема, т.к. при фиксированной деформации (g=const) следует, что g’=0, а t=const, т.е. напряжение при постоянной деформации не уменьшается,  а остается неизменным. Тем не менее, модель тела Кельвина-Фойгта подходит для описания других процессов. Рассмотрим это.

Из последнего уравнения видно, что по мере увеличения времени t  деформация возрастает и асимптотически приближается к величине t0/G. Следовательно, деформация тела Кельвина-Фойгта не развивается мгновенно, а  задерживается вследствие упругого последействия. Величина   G/h характеризует скорость затухания деформации и может быть названа коэффициентом затухания.

Если в течение времени t=t1 , снять нагрузку,  которая была приложена при t=0, то в решении дифференциального уравнения при  t>t1 следует принять t=0, тогда получим


После разгрузки кривая асимптотически приближается  к  нулю.
Постепенное нарастание деформации при постоянной нагрузке, характеризующейся первой ветвью кривой или последовательное уменьшение деформации после снятия нагрузки, как это было уже сказано в § 2.2, называется упругим последействием или эластичностью.

3.8. Вязко-пластическое тело Бингама-Шведова

Примером вязко-пластического тела Бингама-Шведова (см. табл.1.1,п. ж,з) является раствор  желатина  (мармелад,  желе, студень). Раствор  желатина релаксирует отлично от максвеловских тел и постоянно сохраняет небольшое остаточное напряжение сдвига (q), ?т.

Из других веществ,  например, масляная краска есть пластическое тело с таким низким пределом текучести, что давления кисти достаточно для того, чтобы она начала течь как жидкость, но при небольшой толщине слоя собственного ее веса недостаточно, чтобы она могла стекать с вертикальной стенки и тогда она ведет себя как твердое тело.
Бингам для  таких материалов получил реологическое уравнение:

где tТ – предельное напряжение сдвига;
hпл - пластическая вязкость;
?’ – скорость сдвига.
Шведов (для желе) получил уравнение вида:

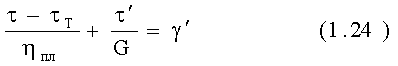
Модель Шведова отличается от модели Бингама тем,  что параллельно телу Сен-Венана присоединено тело  Максвелла,  а  у  Бингама - тело Ньютона.

В соответствие со схемой можно написать:

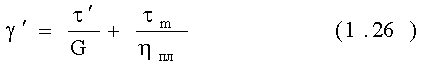
где tm - напряжение в максвеловском элементе,  для которого


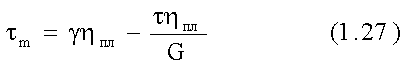
или      

3.9. Тело Фарбмана

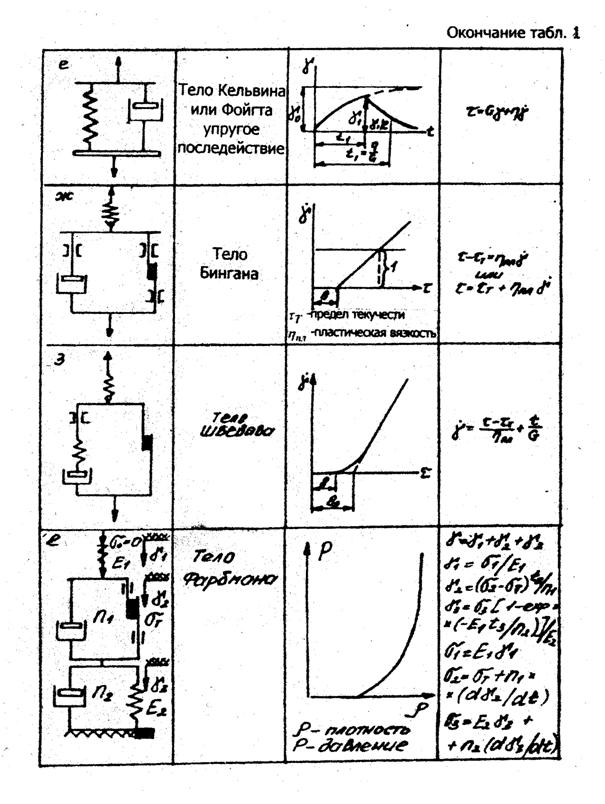
Многие авторы при исследовании  свойств  пищевых  материалов использовали и другие реологические модели (см. табл.1.1,п.е).

Заслуживает внимание реологическая модель тела из спрессованных длиннофрагментных и стебельчатых  насыпных материалов типа чайного листа, лекарственных растений, макаронных полуфабрикатов и др. В результате прессования выше упомянутых материалов Фарбман Г.Я. определил, что можно отметить три этапа.

На первом - из системы вытесняется воздух,  деформация  происходит при ничтожно малых нагрузках. После снятия нагрузки деформации не снимаются. На кривой давления прессования (Р)-  плотность  (r),  участок первого этапа происходит вблизи от оси абсцисс.
Второй этап  характеризуется  интенсивным  развитием упруго-пластических деформаций и быстрым увеличением давления прессования.

На третьем этапе сжимается уже сформированный монолит, в котором преобладают  упругие деформации при резко возрастающем давлении. После снятия нагрузки деформации снимаются с некоторым запаздыванием во  времени, что связано с наличием упругого последействия (эластичности).

Для описания  этих  процессов Фарбман предложил трехзвенную реологическую модель, в которой первый этап прессования моделируется пружиной Е1, малой жесткости - телом Гука с защелкой на конце, второй этап - звеном, состоящим из соединенных параллельно  тел Ньютона (h1) и Сен-Венана (sТ). Первое и второе звенья вместе составляют упругое вязкое пластичное тело Бингама. Деформации в таком теле после снятия нагрузки не исчезают, и в нем сохраняются остаточные напряжения. Третий этап моделируется звеном (тело Кельвина), состоящим из соединенных параллельно тел Ньютона (h2) и Гука (Е2).

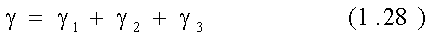
Представленная модель позволяет рассмотреть весь процесс сжатия материала, суммарная деформация которого составляет:

Первое звено - упругое тело. Напряжение прямо пропорционально деформации s1 = Е1g1.

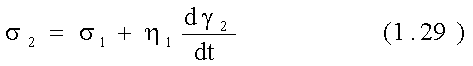
Второе звено - вязкопластическое тело. Тело Сен-Венана ведет себя как твердое тело, и не начнет деформироваться до тех пор, пока напряжения в нем не превысят предел текучести sт (либо пре­дельное напряжение сдвига tт). При s = sт тело начнет течь с некоторой скоростью. После этого вступает в действие тело Ньютона, испытывая напряжение h1(dg2/dt). Таким образом, суммарные напряжения в звене:

где t – время деформации.

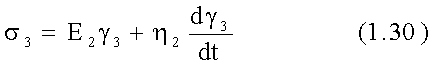
Третье звено - упруго вязкое тело Кельвина, в котором общее напряжение равно сумме напряжений от упругих деформаций sу и вязкого течения sв, т.е.

Решая уравнение суммарной деформации, и учитывая, что скорость деформации dg/dt=g’= =const, t=0, s0=0 находятся выражения для величины деформации  каждого звена модели.

Первое звено:            

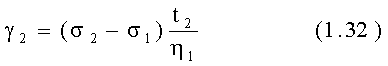
Второе звено:

Третье звено:


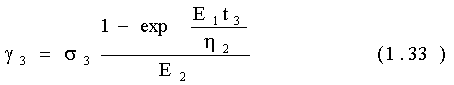
Численные значения характеристик реологических свойств находят из экспериментальных диаграмм "напряжение Р – деформация g" и рассчитывают по выше приведенным формулам.

3.10. Построение обобществленных моделей тел со сложной комбинацией свойств

Можно составить и более сложные сочетания упругих и вязких элементов. При увеличении числа упругих и вязких элементов и усложнении схем их соединения можно получить весьма сложные законы деформирования.
К. Хоэнэмзер и В. Прагер предложили обобщенное линейное тело с реологическим уравнением
a0 + a1s + a2s+ a3g + a4g’ = 0            (1.34), где  s – напряжение;
g – деформация;
g’- скорость деформации;
a0 , a1 , a2 , a3 , a4 – эмпирические коэффициенты.
Для более общего случая уравнение будет иметь вид:

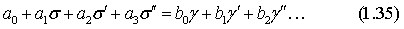
где b0 , b1, b2 – эмпирические коэффициенты.

Анализируя данные эксперимента можно сделать выводы о структуре этого сложного тела:

• Свободный член соответствует наличию тела Сен-Венана;
• Порядок деформационного уравнения  получается  не  больше числа вязких элементов схемы;
• Отсутствие упругой непрерывной связки в  схеме  указывает на то,  что при длительном действии нагрузки деформация неограниченно возрастает;
• В  схемах  с  упругой непрерывной  связью при длительном действии нагрузки деформация стремиться к некоторому  предельному значению, соответствующему "длительному модулю упругости",  величина которого может быть определена по схеме  при  исключении  из нее всех вязких элементов;
• При быстром приложении нагрузки  деформация  определяется "мгновенным" модулем упругости:  его можно получить из схемы, полагая, что все вязкие элементы жесткие.