

Основные понятия инженерной реологии
2.1. Аксиомы реологии
ПЕРВАЯ аксиома. Под действием всестороннего равномерного давления все материалы ведут себя одинаково - как идеально упругие тела.
Изменение линейных размеров произойдет за счет упругой деформации, т.е. при снятии давления линейные размеры и плотность этих тел примут первоначальные значения.
Различия в реологических свойствах проявляются только при деформации, изменяющей форму тела-деформации формоизменения.
ВТОРАЯ аксиома. Каждый материал обладает всеми реологическими свойствами, хотя и в разной степени. К основным реологическим свойствам относятся: упругость, пластичность, вязкость, прочность.
Эти свойства у одного и того же материала в зависимости от его состояния и условий нагружения могут проявляться в большей или меньшей мере. Поэтому, в первую очередь необходимо выяснить, какие свойства исследуемого материала при заданных условиях являются основными, определяющими.
2.2. Термины и определения реологии
Вязкость - текучесть. Вязкостью называется мера сопротивления течению жидкости; она равна отношению напряжения сдвига к скорости сдвига. Текучестью называется величина обратная вязкости.
Упругость – свойство практически мгновенно полностью восстанавливать первоначальные размеры при мгновенном снятие приложенной нагрузки (остаточные деформации отсутствуют).
Пластичность вызывается деформацией, т.е. относительным смещением частиц, при котором не нарушается непрерывность самого тела. Пластичность – это способность течь при напряжении выше критического, называемого пределом текучести, обнаруживая развивающиеся во времени остаточные деформации. При напряжении ниже критического, тело ведет себя как упругое.
Деформации делят на упругие, т.е. исчезающие после снятия нагрузки, и на остаточные, необратимые, не исчезающие после удаления нагрузки. Остаточные деформации, не сопровождающиеся разрушением материала, называются пластическими, а сами материалы - пластическими.

Напряжение. Под действием внешних сил происходит изменение формы и размеров тела. Все реальные тела деформируются. Деформация тела сопровождается возникновением внутренних сил взаимодействия между частицами тела. Мера интенсивности внутренних сил является напряжение P.
где DP - внутренняя сила;
DF - элементарная площадка.
Проекция полного напряжения на нормаль называется нормальным напряжением - s; составляющая в плоскости сечения – касательным напряжением - t.
Элемент в условиях объемного напряженного состояния может быть изображен в виде параллелепипеда (см. рис. 1.1)
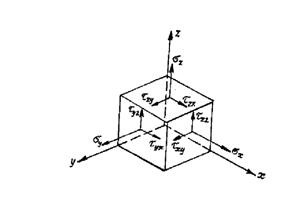
Рис. 1.1. Действие напряжений на параллелепипед
в напряженном состоянии:
sх, sy, sz - нормальные напряжения;
tzx, txz, tzy, tyz, txy, tyx - касательные напряжения.
Закон парности касательных напряжений говорит, что касательные напряжения взаимно перпендикулярных площадок равны и направлены либо к ребру, либо от ребра.
tzx = txz ; tzy= tyz ; txy = tyx (1.2)
Напряжение сдвига - сопротивление тела действию приложенной силы. Напряжение сдвига равно отношению приложенной силы к величине площади сдвига. Минимальная сила для осуществления сдвига определяется предельным напряжением сдвига ?т или, как ниже будет применятся его обозначение - ?. При сдвиге изменяется форма тела при постоянном объеме. Сдвиг получается от действия на гранях элемента касательных напряжений ? (см. рис.1.2)
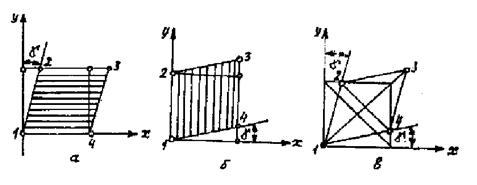
Рис.1.2 Деформация сдвига:
g1, g2, g3 - углы сдвига.
В идеально упругом теле упругие деформации при постоянной нагрузке сохраняются без изменений. В жидкости деформации и соответствующие им напряжения рассасываются быстро, а для воды мгновенно.
При мгновенном воздействии любая вязкая жидкость ведет себя как твердое тело, а при медленных воздействиях она успевает релаксировать и ведет себя как жидкое тело. Это явление называется фазовым переходом.
Релаксация - постепенное уменьшение действия напряжений s, t до нуля или до какой-нибудь величины при не изменяющейся во времени t деформации. Эта величина определяется упругой частью общей деформации, которая достигается не сразу, а постепенно (в течение времени релаксации t).
Ползучесть - постепенное нарастание во времени t суммарной деформации e графически приведено на рис.1.3 (участок БВ).
Упругое последействие или эластичность - изменение упругой деформации во времени, когда она или постепенно нарастает до некоторого предела после приложения нагрузки (восстановление структуры), или постепенно уменьшается после ее снятия (разрушение структуры), см. рис.1.3 (участки АБ и ВГ).
Пластичность – способность течь при напряжении выше критического, называемого пределом текучести, обнаруживая развивающиеся во времени остаточные деформации. При понижении ниже критического тело ведет себя как упругое.
Вязкость – проявляется в том, что при сколь угодно малом постоянном напряжении деформация тела непрерывно увеличивается пропорционально времени.
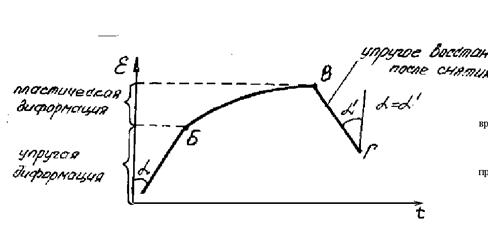
Рис. 1.3 Изменение деформации в течение времени t под действием нагрузки:
АБ - участок упругих деформаций при нагрузки;
БВ - участок пластических деформаций;
ВГ - участок восстановления упругих деформаций при нагрузке;
В - точка снятия нагрузки.
Абсолютно жидкое тело от абсолютно твердого тела отличается весьма малой силой сцепления между отдельными частицами. Промежуточное положение занимают вязкие и пластичные тела.
