Назад: 5.1 Задачи динамики регулирования
5.2
Элементарные звенья цепи регулирования и их уравнения
Для анализа динамики САР необходимо знать свойства
элементов, из которых состоит система. Элементы системы могут существенно
отличаться друг от друга по своей физической природе и конструктивному
оформлению. Однако элементы различных систем могут быть описаны одинаковыми
дифференциальными уравнениями. При исследовании динамики САР принято деление
систем на элементы не по физической природе или функциональному назначению, а
по динамическим свойствам (виду уравнения). Под различными звеньями понимают
элементы, отличающиеся между собой поведением в динамике, т.е. переходными
функциям под действием типовых сигналов, которые описываются линейными
дифференциальными уравнениями не выше второго порядка.
Типовые
входные сигналы. Для исследования
динамических свойств элементов и систем необходимо решить дифференциальное
уравнение и исследовать его. Это возможно, если известна входная величина хвх(t)
как функция времени. В реальных условиях при работе САР входная величина
сигнала каждого элемента является случайной функцией времени. Поэтому для
исследования элементов (сравнение их свойств при одинаковых условиях)
принимается несколько типовых сигналов, отражающих различные стороны совокупности
входных случайных сигналов. Входные сигналы называют возмущающими, а выходные
сигналы, возникающие в результате их воздействия, – реакцией на эти возмущения.
Типовые формы сигналов показаны на рис. 5.1.
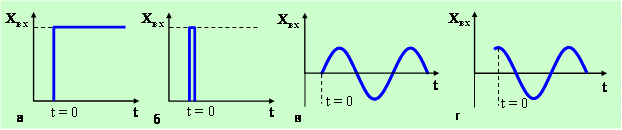
Рис.5.1 Типовые входные сигналы: а – ступенчатая
функция;
б – импульсная функция; в – синусоидальная, г –
косинусоидальная
Ступенчатая толчкообразная
функция, ступенчатый сигнал (рис.5,1,а).
Эта функция скачком в момент t = 0 достигает величины А = const и далее
остается постоянной. Это значит, что хвх(t) = А при t ³ 0 и хвх(t) = 0 при t ≤ 0. Иногда для
ступенчатой функции используется обозначение хвх(t) = А1(t). Функция
1(t) называется единичной ступенчатой функцией;
Импульсная функция (рис.5.1,б) хвх(t) = А1¢(t), где А = const; 1¢(t) – импульс бесконечно большой амплитуды и
бесконечно малой длительности, так что  .
.
Гармоническая функция (рис.5.1,в,г) может задаваться в вещественной форме в
виде гармонической функции – синусоидальнуой хвх(t) = Авхsin(ωt
+ φ) (рис.5.1,в), или косинусоидальной – хвх(t) = Авх
cos(ωt + φ) (см. рис.5.1,г), где Авх – амплитудная
величина входного сигнала; ω = 2p/Т – круговая частота колебаний хвх(t); Т –
период колебаний.
Комплексная функция хвх(t) = Авхе j (ωt +
φ).
Всё многообразие звеньев систем автоматики сводится к
следующим звеньям: безынерционное усилительное, апериодическое, колебательное,
дифференцирующее, интегрирующее.
Безынерционное усилительное звено (прил.2). В этом звене величина Хвых в каждый
момент времени пропорциональна входной величине Хвх. Уравнение
звена:
Хвы х = kХвх,
где k – статический коэффициент
усиления звена или его передаточный коэффициент.
Примером такого звена может служить полупроводниковый
усилитель, механический рычаг, редуктор, если пренебречь их массой и силой
трения.
Апериодическое,
или инерционное звено первого порядка (прил.2). Уравнение
динамики такого звена описывается уравнением
![]()
![]() , (5.1)
, (5.1)
где
Т – постоянная времени; k – передаточный коэффициент звена.
Примером такого звена может
служить термопара, генератор постоянного тока, электродвигатель, если входной
величиной служит ток якоря, а выходной – угловая скорость вала. Апериодическим
звеном описывается большинство элементов сварочного оборудования. Постоянная
времени обусловлена массой, моментом инерции, индуктивностью, емкостью и
другими параметрами элемента.
Апериодическое звено второго порядка. Уравнение звена
имеет вид
![]() , (5.2)
, (5.2)
где
Т1 и Т2 – постоянные времени звена.
Примерами таких звеньев могут служить электрические
контуры, содержащие несколько индуктивностей, электрические двигатели,
магнитные усилители.
Колебательное
звено (прил.2). Уравнение устойчивого звена:
![]() , (5.3)
, (5.3)
где а – коэффициент демпфирования
колебаний (затухания), характеризующий скорость затухания колебаний, находится
в пределах 0 < а > 1. Чем больше а, тем быстрее затухают колебания.
Дифференцирующее
звено (прил.2). Выходная величина его пропорциональна производной во
времени от входной величины, т.е. реагирует на скорость изменения входной
величины. Различают идеальное и реальное дифференцирующие звенья. Идеальное
(безынерционное) звено описывается уравнением
![]() (5.4)
(5.4)
Примером такого звена может служить тахогенератор
постоянного тока, у которого э.д.с. пропорциональна скорости вращения вала
якоря при холостом ходе или в режиме, близком к нему, используемый в САР для
определения скорости подачи электродной проволоки, САР стабилизации скорости
поворота изделия во вращателях и т.д.
На практике чаще встречаются реальные дифференцирующие
звенья, динамика которых описывается уравнением
![]() (5.5)
(5.5)
Оно представляет собой последовательное соединение
идеального дифференцирующего звена с апериодическим. В качестве примера такого
звена может быть пассивная RC-цепочка и дифференцирующий трансформатор.
Интегрирующее
звено (прил.2). Выходная величина в идеальном интегрирующем звене
пропорциональна интегралу во времени от входной величины:
![]() (5.6)
(5.6)
Если возмущающее воздействие на входе звена имеет вид
единичного скачка, то выходная величина изменяется по закону
![]()
т.е.
линейно зависит от времени.
Примерами идеального интегрирующего звена могут быть
электродвигатель (при пренебрежении электромеханической постоянной времени),
если вход – напряжение питания якоря, а выходная величина - угол поворота
вала), а также звено, связывающее длину дуги при сварке плавящимся электродом
со скоростью подачи проволоки.
Реальное (инерционное) интегрирующее звено описывается
уравнением
![]() . (5.7)
. (5.7)
Примером реального интегрирующего
звена является электродвигатель, если учитывается только одна наибольшая
постоянная времени его и за входное воздействие считается напряжение на якоре,
а за выходное - угол поворота якоря.
С целью упрощения методов расчетов и проектирования
САУ уравнения динамики объектов или их устройств записывают не в виде
оригинальных функций, а в виде изображений функций, получаемых с помощью
прямого преобразования Лапласа – операционное исчисление. При этом
предполагается, что до начала воздействия входного сигнала, т.е. при t ≤
0, система находилась в покое, выходные величины и их производные равны нулю.
Операторной формой записи дифференциальных уравнений называется
такая их своеобразная запись, когда символы операций дифференцирования и
интегрирования заменяют некоторым числом «р», которое понимается как некоторое
комплексное число (a + jb), после чего операции дифференцирования и интегрирования
заменяют алгебраическими операциями над числом «р». Переход к операторной форме
позволяет намного облегчить процедуру определения и решения общего
дифференциального уравнений системы в целом. Преимущество операционного метода
по сравнению с классическим заключается в упрощении операций дифференцирования
и интегрирования, сведении их к умножению и делению и решении простых алгебраических
уравнений.
Передаточной функцией звена или системы называют
отношение изображения выходной величины к изображению входной величины при
нулевых начальных условиях и обозначают W(p) = Q(р)/ Р(р). Передаточная функция
является дробно-рациональной функцией аргумента (р), и свойства системы
отображаются коэффициентами полиномов Р(р) и Q(р). Знаменатель передаточной
функции – многочлен Р(р) – является характеристическим полиномом
дифференциального уравнения входной величины рассматриваемой системы (правая
часть уравнения), Q(р) – полиномом выходной величины (левая часть уравнения).
Чтобы перейти к операторной форме записи достаточно заменить в соответствующих
дифференциальных уравнениях символы d/dt, d2/dt2, òd/dt соответственно символами p, p2, 1/p.
Передаточные функции типовых звеньев приведены в прил.2.
Для определения передаточной функции динамической
системы или группы звеньев необходимо:
·
взять за основу
функциональную схему системы, расчленить её на звенья, выявить и уточнить
входные и выходные величины и их размерности для каждого входящего в систему
динамического звена и записать дифференциальные уравнения для объекта регулирования
и элементов системы регулирования;
·
привести систему
уравнений к начальным условиям и (при необходимости и возможности) нелинейные
уравнения линеаризировать;
·
составить
уравнения статики для звеньев;
·
получить
уравнения в отклонениях, записывая в левой части выходную величину и её производные,
а в правой – все остальные члены;
·
по совокупности
уравнений звеньев составить уравнения динамики для системы в целом, т.е. найти
решение относительно управляемого параметра (или ошибки) системы;
·
записать
уравнение в операторной форме, т.е. заменить выходную и входную функции времени
их изображениями по Лапласу;
·
преобразовать
уравнение так, чтобы получить отношение изображения выходной величины к изображению
входной величины, т.е. записать W(p) в виде дробно-рациональной
функции.
При составлении W(p) для системы применяют
определенные правила составления передаточных функций в зависимости от способа
соединения входящих в неё звеньев (алгебра передаточных функций) и методы
преобразования структурных схем[1].
Различают последовательное, параллельное включение звеньев направленного
действия и параллельно-встречное соединение (рис.5.2).
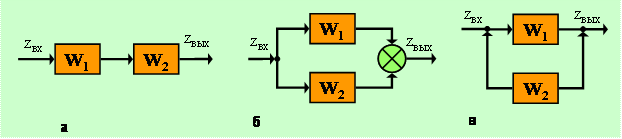
Рис. 5.2. Схемы соединения звеньев: а –
последовательное;
б – параллельное направленного действия; в – параллельно–встречное
При последовательном соединении звеньев,
когда выходная величина каждого предыдущего звена является входным воздействием
последующего, передаточная функция системы или эквивалентного звена равна
произведению передаточных функций всех звеньев:
![]() .
.
При параллельно согласованном соединении
звеньев (при одном направлении прохождения сигнала), когда на вход всех звеньев
действует один и тот же сигнал, а выходная величина суммируется, передаточная
функция эквивалентного звена или системы равна алгебраической сумме
передаточных функций всех звеньев
![]() .
.
При параллельно-встречном соединении
звеньев образуется замкнутый контур прохождения сигнала и создается эффект
обратной связи. Для замкнутого контура передаточная функция определяется по
формуле
![]() .
.
Далее: 5.3 Частотные характеристики
типовых звеньев и систем