Назад: 1.2.2 Замкнутые системы управления

1.3 Разновидности систем автоматического управления с обратными связями

1.3.1 Принципы построения САУ

В зависимости от того, как связаны в САР контролируемая величина и регулирующая, все системы управления можно разделить на две группы в зависимости от места приложения регулирующего воздействия: оно может быть направлено на компенсацию отклонения регулируемой величины либо на ликвидацию возмущения, которое вызвало это отклонение.

Принцип регулирования по отклонению. Большая часть САР построена на основе контроля отклонения регулируемого параметра от заданного – (принцип Ползунова - Уатта) [6]. В таких системах контролируется (измеряется) регулируемая величина х(t). Она сравнивается с заданным для данного момента управления воздействием z(t), в результате чего выявляется ошибка e(t) = х(t) – z(t). Обобщенная функциональная схема системы показана на рис. 1.6,а. Реакция системы на возникшее изменение состояния является действием ее, направленным на ликвидацию отклонения e(t).

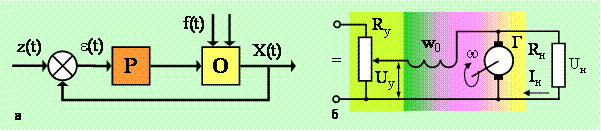
Рис.1.6. Система автоматического управления по отклонению:

а – функциональная схема регулирования; б – принципиальная электрическая схема генератора; z(t) – задающая величина регулируемого параметра; х(t) – регулируемая величина; Р – регулятор; О – объект регулирования; f(t) – возмущение

Система контролирует состояние объекта по одному из параметров и при его изменении воздействует не на само возмущение f(t), оказывающее влияние на систему и являющееся первопричиной этого изменения, а на контролируемый параметр непосредственно или через объект. Суть принципа регулирования заключается в том, что регулятор измеряет отклонение регулируемой величины от заданной величины и, перемещая регулирующий орган, воздействует на объект регулирования таким образом, чтобы свести отклонение (ошибку) к минимуму. Следовательно, регулятор приходит в действие только при возникновении отклонения независимо от причины его вызвавшей.

Рассмотрим в качестве примера систему регулирования напряжения сварочного генератора (рис.1.6,б). Задача ее – поддерживать на постоянном уровне напряжение U_н на нагрузке R_н. Известно, что это напряжение зависит от частоты вращения якоря генератора w и от напряжения на обмотке возбуждения w₀. Схема построена так, что напряжение возбуждения является разностью между напряжением уставки U_у, снимаемым с потенциометра-задатчика R_у, и напряжением на нагрузке U_н, т.е. U_в = U_у – U_н.

При заданной нагрузке R_н, перемещая ползунок потенциометра-задатчика R_у, можно найти такое положение, при котором в установившемся состоянии напряжение на нагрузке имеет требуемое значение U_нo. Пока это напряжение соответствует заданному значению, состояние системы остается неизменным, она неподвижна. Если под действием каких-либо причин (изменение нагрузки, частоты вращения якоря генератора и др.) напряжение на нагрузке изменится, то система придет в движение, начнется переход от ее старого устойчивого состояния в новое.

Допустим, что внешнее возмущение выразилось в увеличении нагрузки, т.е. в уменьшении ее сопротивления R_н. В первый момент это вызывает снижение напряжения на нагрузке до некоторого значения U_н1 из-за возрастания тока нагрузки, а значит, и падения напряжения на внутреннем сопротивлении якоря генератора. Этот параметр система контролирует, так как непрерывно сравнивает его с установкой U_у. Поэтому отклонение регулируемой величины от заданной сразу же обнаруживается системой. Проявляется это в резком увеличении напряжения U_в. Начинается регулирование, заключающееся в том, что под действием возросшего потока возбуждения генератора напряжение на нагрузке восстанавливается.

Аналогично система действует в случае когда изменение выходного напряжения вызвано изменением частоты вращения якоря генератора. Уменьшение скорости ведет сначала к снижению U_н, затем при регулировании оно восстанавливается вследствие возросшего потока возбуждения, так как U_в = U_у – U_н. Так же система действует и в том случае, когда одновременно изменяется величина тока и напряжения. Описанная система и подобные ей поддерживают на выходе с определенной точностью заданный регулируемый параметр независимо от того, какие возмущения действуют, где они приложены и сколько их действует одновременно.

Принцип регулирования по возмущению. Этот принцип регулирования заключается в том, что регулятор осуществляет регулирующие воздействия по величине возникшего возмущения. Основным обычно является возмущение по нагрузке, поэтому часто реализуют систему регулирования по нагрузке.

Принцип регулирования по возмущению рассмотрим на примере сварочного генератора со смешанной системой возбуждения (с двумя обмотками, рис.1.7). Одна из них (w₀) независимая, а другая (w_к) включена согласно с w₀ и последовательно с якорем генератора, и по ней, следовательно, течет ток нагрузки I_н (см. рис.1.7,б) [7].

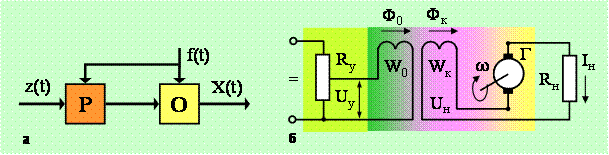
Рис.1.7. САУ с обратной связью по возмущению:

а – функциональная схема регулирования; б – принципиальная электрическая схема генератора со смешанным возбуждением

Напряжение U_н на нагрузке R_н зависит от суммарного потока возбуждения Ф_в = Ф₀ + Ф_к, часть которого Ф_к определяется током нагрузки в обмотке w_к, а другая Ф₀ выбирается с помощью потенциометра R_у такой, чтобы при заданной нагрузке R_н на ней имелось необходимое напряжение.

При действии другого возмущения система регулирования оказывается неработоспособной. При возмущении, например, по частоте вращения вала генератора w вследствие падения напряжения в сети, питающей приводной двигатель, напряжение на нагрузке также падает, но уменьшается при этом и ток нагрузки. Получается так, что вместо необходимого увеличения суммарного потока возбуждения он уменьшается, и напряжение U_н падает еще больше. При других возмущениях система также не работает. Система работоспособна только при контролируемом возмущении по нагрузке. Отсюда следует, что применение САР по возмущению менее целесообразно, чем системы, построенной по принципу регулирования по отклонению. Особенно малоэффективен этот принцип регулирования, когда на систему действует несколько существенных возмущений. В системе регулирования по возмущению регулируемая величина не контролируется, и поэтому система оказывается разомкнутой по регулируемому параметру и замкнутой по контролируемому возмущению f_i(t). Отсюда следует, что при регулировании по возмущению необходимо знать, как связано изменение регулируемого параметра с изменением возмущения, чтобы можно было управлять регулируемым параметром х(t) через воздействие на f_i(t). Регулирующее воздействие здесь формируется на основе информации об одном из контролируемых возмущений f_i(t). Регулируемая величина оказывается защищенной от действия только одного выбранного возмущения f_i(t), по нему одному есть замкнутый контур регулирования. По другим возмущениям система разомкнута – нет информации об их величинах, и поэтому неизвестно, действуют ли они в данный момент.

Система регулирования по возмущающему воздействию работает по принципу компенсации только одного заранее выбранного возмущения. Эти системы еще называют системами компенсации.

Преимуществом этого метода является то обстоятельство, что воздействие возмущения на регулируемую величину может быть устранено до того, как произошло отклонение регулируемой величины.

Комбинированная система регулирования. В этих системах одновременно используются принцип регулирования по отклонение и по нагрузке. Эти системы называют многоимпульсными системами. На рис.1.8 показаны функциональная схема комбинированной системы регулирования и принципиальная электрическая схема сварочного генератора с двумя обмотками возбуждения: независимой w₀ и последовательной w_к, действующих согласно.

Рис. 1.8. Комбинированная система регулирования:

а - функциональная схема; б - принципиальная электрическая схема

Комбинированная система регулирования реагирует на отклонение напряжения на нагрузке и на изменение тока нагрузки. Такие системы позволяют повысить точность поддержания заданного значения регулируемой величины.

По характеру изменения задающего воздействия z(t), подаваемого на вход системы, или требуемого значения выходной величины замкнутые САУ подразделяются на три класса: системы стабилизации, следящие системы, системы программного управления.

Далее: 1.3.2 Системы стабилизации