Раздел III. ТЕПЛОВЫЕ ОСНОВЫ СВАРКИ

НАЗАД: 3.2.1. Расчетные схемы нагреваемых тел и источников тепла

3.2.2. Нагрев мощными быстродвижущимися источниками

3.2.2.1. Тепловые характеристики сварочной дуги

Считают, что вся электрическая энергия, расходуемая при дуговой сварке, переходит в тепловую энергию. Поэтому полная тепломощность дуги q определяется уравнением

q = IU, Дж/с, (3.9)

где U – напряжение дуги, В;

I – ток дуги, А.

Но из этой тепломощности лишь часть расходуется на нагрев свариваемых деталей, которая называется эффективной тепломощностью нагрева изделия q_и:

q_и = q×h_и; Дж/с, (3.10)

где h_и – эффективный к.п.д. нагрева изделия.

Значения h_и определяются экспериментально и для некоторых способов дуговой сварки приведены в табл.5.

Таблица 5. Значения эффективного к.п.д. нагрева изделия

Способ сварки	Значения hи
Сварка неплавящимся угольным или вольфрамовым электродом	0,45¸0,60
РДС плавящимся электродом	0,70¸0,85
Сварка плавящимся электродом в среде углекислого газа	0,78¸0,92
Автоматическая сварка под флюсом	0,80¸0,95

Величина h_и растет с уменьшением напряжения дуги и увеличением тока дуги (по мере погружения дуги в основной металл).

Как видно из таблицы, значения h_и при сварке плавящимся электродом значительно выше, чем при сварке неплавящимся электродом. Это объясняется тем, что при сварке плавящимся электродом часть тепла, получаемая от дуги плавящимся электродом, вместе с каплями расплавленного электродного металла поступает в сварочную ванну.

Распределение эффективной тепловой мощности нагрева изделия неравномерно по пятну нагрева (см. рис. 29) и подчиняется уравнению:

Дж/с×см² (3.11)

где q₂(r) – удельный тепловой поток в зависимости от расстояния r (см) от оси источника тепла;

k – коэффициент сосредоточенности, определяемый экспериментально, 1/см²;

q_{2 max} – максимальный удельный тепловой поток по оси источника тепла, т.е. дуги, Дж/см²×с.

(3.12)

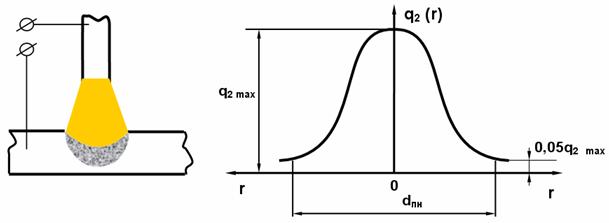
Рис. 29. Распределение удельного теплового потока по пятну нагрева

Диаметр пятна нагрева d_nн соответствует краевым значениям удельного теплового потока, равным 0,05 q_{2 max}.

Тогда можно записать:

q_{2 max} × e (3.13)

В этом случае r = d_nн/2.

Прологарифмируем уравнение (3.13):

ln 0,05 = – kr².

Так как ln 0,05 = – 3, получим

kr² = 3, т.е. d_nн = . (3.14)

Для дуговых процессов значения k лежат в пределах (1¸6) 1/см². Это большие значения коэффициента сосредоточенности, поэтому дугу считают точечным источником тепла.

ДАЛЕЕ: 3.2.2.2. Распределение тепла при действии мощных быстродвижущихся источников тепла