ЛЕКЦИЯ 4

ТЕМА: Линейный  закон   фильтрации

Экспериментально установлено, что потери напора при фильтрации зависят линейно от скорости фильтрации. Эта зависимость получила название закона сопротивления при фильтрации или линейного закона фильтрации (закон Дарси).

Допустим, имеем цилиндрическую трубу диаметром d, заполненную пористым материалом, в которой происходит фильтрация жидкости (суспензии) в направлении, указанном стрелкой А(рис.5).

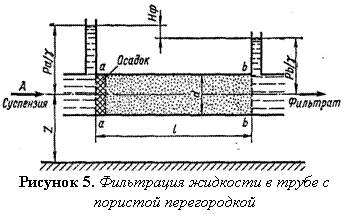
В соответствии с уравнением Бернулли для сечений а—аи b—bможем записать выражения полного напора:

где Н_а-а — полный напор в сечении а—a; H_b-b — полный напор в сечении b—b; Z— высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости; р_а — давление гидродинамическое в сечении а—а; р_ь — давление гидродинамическое в сечении b—b; у — удельный вес фильтрующей жидкости; v_a — скорость фильтрующейся жидкости в сечении а—а; v_b — скорость фильтрующейся жидкости в сечении b—b; g— ускорение свободного падения.

Скоростной напор при фильтрации является крайне малой величиной по сравнению с пьезометрическим напором, поэтому им пренебрегают.

Потери напора на участке l между сечениями а—а и b—b составят

Математическое выражение линейного закона фильтрации (закона Дарси):

где Q - расход фильтруемой жидкости (суспензии); K_ф— коэффициент фильтрации; F— площадь сечения трубы; H_ф — потери напора на участке фильтрации длиной l; l — длина участка филь­трации.
Коэффициент фильтрации имеет размерность скорости и харак­теризует свойства фильтровального материала применительно к конкретному виду фильтруемой жидкости.

Отношение Н_ф / lпредставляет собой градиент напора или пьезометрический уклон. Обозначив его через J, получим выражение закона Дарси в следующем виде:

Часто при исследовании процессов фильтрования необходимо знать свойства фильтрующей среды (фильтрующей перегородки), не привязывая их к конкретным видам фильтрующей жидкости. Способность фильтрующей среды пропускать жидкость в зависимости от количества, размеров и конфигураций поровых каналов и называется проницаемостью. Коэффициент проницаемости — величина, численно равная скорости фильтрования жидкости, с вязкостью, равной единице, при перепаде давлений, равном единице, через фильтрующий слой толщиной, равной единице. Коэффициент проницаемости К_пн связан с коэффициентом фильтрации соотношением:

где К_пн— коэффициент проницаемости; m — коэффициент абсолютной (динамической) вязкости фильтруемой  жидкости;  у— удельный вес фильтрующей жидкости; n — коэффициент кинематической вязкости.

Заменяя коэффициент фильтрации коэффициентом  проницаемости,   получим

Математический анализ течения жидкости в пористых средах обычно сводят к анализу линейного закона фильтрации. В диффе­ренциальной форме этот закон можно записать в следующем виде:

где dp / dx— перепад давления на единицу длины участка фильтрации.

Проинтегрировав  в граничных условиях от р₁ до р₂ и от х=0 до х=l,получим

где р₁— давление на входе в фильтрующую среду; р₂ — давление на выходе из среды.

При радиальном движении фильтруемой жидкости (суспензии) можем записать закон Дарси в дифференциальной форме:

где r— расстояние относи образца;  h— высота полого цилиндрического  фильтра.

Проинтегрировав в граничных условиях от р₁до р₂и от r_вн до r_н, получим

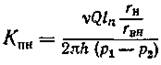
Предложен ряд формул для определения коэффициента проницаемости, однако, они не дают достаточно точных результатов. Поэтому определение коэффициента проницаемости желательно проводить экспериментальным путем.

Коэффициент проницаемости не зависит от свойств жидкости и характера ее движения; он определяется только геометрическими размерами пор фильтрующего материала. Но опытные данные свидетельствуют, что коэффициент проницаемости в определенной мере зависит и от свойств фильтруемой жидкости и фильтрующего материала. Эта зависимость объясняется следу­ющими факторами:

- при фильтрации жидкостей в порах образуются адсорбционные пленки, что уменьшает коэффициент проницаемости;
- в процессе фильтрации минеральных масел в фильтрующем материале образуются зоны застойной жидкости, объем которой может достигать 13—37%;
- рабочие жидкости гидроприводов могут содержать до 15—18% воздуха в нерастворенном состоянии, пузырьки которого оказывают дополнительное сопротивление фильтрации   (эффект Жамена).

При исследовании явлений фильтрации необходимо учитывать, что линейный закон фильтрации справедлив лишь при относительно малых скоростях движения жидкости при фильтрации. При значительном увеличении скорости движения жидкости линейный закон фильтрации нарушается.

Любую пористую перегородку, применяемую для фильтрования, следует рассматривать как среду, имеющую три вида пор (рис.6).

Сквозные поры 1 пронизывают пористую перегородку насквозь. Они способны задерживать механические загрязнения рабочей жидкости,   пропуская   ее.   Сквозные   поры   могут  задерживать твердые частицы, имеющие размер меньше, чем наименьшая площадь сечения сквозной поры. Внутренние (глухие) поры 2, не сообщаются   с   наружной поверхностью пористой перегородки. Слепые поры 3сообщаются с одной из наружных поверхностей пористой перегородки и заканчиваются внутри  нее.

Фильтрование рабочей жидкости происходит только через сквозные поры пористой перегородки. Не следует путать понятия «фильтрование» и «фильтрация».

Фильтрация— самопроизвольное или преднамеренное прохождение жидкости через пористую среду, которое может сопро­вождаться отделением взвешенных частиц.

Фильтрование— преднамеренно осуществляемый процесс фильтрации для разделения жидких неоднородных систем.

Пористость фильтрующей перегородки характеризуется общим коэффициентом   пористости

где m_общ— коэффициент пористости фильтрующей перегородки; V_п — объем всех пор фильтрующей перегородки; V— объем фильтрующей перегородки, включающий объем всех пор и объем материала перегородки:  , где V_м— объем материала фильтрующей перегородки.

Помимо общего коэффициента пористости существуют коэффициенты внешней и внутренней пористости. Коэффициент внешней пористости характеризует отношение объема сквозных и слепых пор к объему фильтрующей перегородки:

где m₁— коэффициент внешней пористости;  V_ск, V_сл — объем сквозных и слепых пор.

Обычно коэффициент внешней пористости m₁ называют просто коэффициентом пористости, так как фильтрование РЖ происходит лишь через сквозные поры.

При изучении процессов фильтрования пользуются понятием средних скоростей течения и давления жидкости в  пористой  перегородке.

Среднюю скорость фильтрования через пористую перегородку определяют как некоторую условную скорость, которую имела бы рабочая жидкость при движении через пористую перегородку, заполняя объем всех пор (V_п)и объем материала перегородки (V_M)при соблюдении условия равенства расхода жидкости Qчерез элементарную площадку Fпористой перегородки действи­тельному расходу рабочей жидкости:

где v_cp— средняя скорость фильтрования; Q — действительный расход рабочей жидкости через элементарную площадку пористой перегородки  F.

Предположим, что поры равномерно распределены по объему пористой перегородки. Тогда элементарная площадка пористой перегородки, занятой порами, будет  равна F_п= m₁F.

Среднюю скорость жидкости в порах площадки или поровую скорость жидкости можно определить согласно гипотезе Дюпюи-Форхгеймера:

При фильтровании рабочей жидкости через пористую перегородку сопротивление перегородки проходу жидкости растет, так как уменьшается эффективное сечение пор. Уменьшение эффективного сечения пор происходит даже в случае, когда раз­меры  загрязняющих   жидкости   частиц  меньше   размеров   пор.