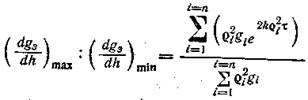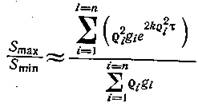ЛЕКЦИЯ №11-12

ТЕМА: Центробежная очистка

Скорость осаждения материальной частицы в центробежном поле и вязкой среде функционально связана с числом Рейнольдса Re, характеризующим отношение сил инерции к силам трения, возникающим при движении частицы.

При Re < 1 для определения скорости осаждения частицы может быть применен закон Стокса, согласно которому скорость осаждения частицы в центробежном поле выразится зависимостью:

где p - эквивалентный радиус частицы; 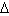- разность  плотности  частицы  и  жидкости; r- расстояние от частицы до оси вращения; 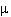- динамическая   вязкость   жидкости.

Как известно,

где y_f— плотность среды  (жидкости).

Отсюда условием осаждения частицы по закону Стокса является:

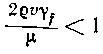
Подставляя в выражение v из закона Стокса и решая его относительно p, получаем условие осаждения частицы в цен­тробежном   поле:

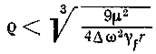
При Re >1000 скорость осаждения определяют по формуле Грасгоффа-Реттингера.

Формул для определения скорости осаждения частицы при 1 < Re < 1000 не имеется. Поэтому рассмотрим общий способ определения скорости осаждения частицы в центробежном поле при  разных  значениях  Re.

Частица, движущаяся в жидкости, испытывает лобовое сопро­тивление, которое определяется по закону Ньютона:

где  С_х- коэффициент  лобового  сопротивления; v- скорость движения частицы; d- диаметр   частицы; y_f- плотность  среды. Коэффициент лобового сопротивленияявляется функцией числа   Рейнольдса  и  зависит  от  формы  и  положения   частицы в   среде.

Выражая скорость осаждения частицы в жидкости через число Рейнольдса:
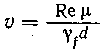      получаем      

Относительное движение частицы в центробежном поле можно выразить следующим дифференциальным уравнением:

где т - масса   частицы;  - приведенная масса частиц в жидкости (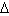— разность плотности частиц и жидкости). Для упрощения силой инерции частиц можно пренебречь, так как ускорение частицы невелико. Тогда уравнение примет вид:

Определив из уравнения С_х Re² и найдя по справочной диаграмме C_xRe² = f(Re), число Рейнольдса,  можно определить скорость осаждения частицы.

Для оценки эффективности работы центрифуги и скорости осаждения частиц в центробежном поле большое значение имеет так называемый фактор  разделения.

Фактор разделения представляет собой отношение ускорений центробежного  и гравитационного полей:

где Е—ускорение центробежной  силы; g—ускорение силы тяжести. Приведенные рассуждения основаны на предположении, что осаждающиеся частицы загрязнения масла имеют шарообразную форму.

В действительности частицы загрязнения асимметричны. Это обстоятельство привело к необходимости введения эквивалентного радиуса, т. е. радиуса такой воображаемой шарообразной частицы, которая при прочих равных условиях имела бы наблю­даемую для  реальной  частицы  скорость осаждения.

При условии осаждения частицы по закону Стокса фактор разделения выражается отношением скоростей осаждения частицы в центробежном и гравитационном полях:

где   v - скорость осаждения  частицы в центробежном поле; v₀ - скорость осаждения  частицы  в  гравитационном  поле.

В современных ультрацентрифугах фактор разделения дости­гает 250 000, в обычных промышленных фильтрующих центрифугах не превосходит 1500. По принятой в литературе классификации процессы центрифугирования в сплошных роторах разделяются по количеству твердой фазы в суспензии на центрифугальное осветление и отстой­ное центрифугирование.

При центрифугальном осветлении объемная концентрация твердой фазы в суспензии незначительна и обычно не превышает нескольких процентов; это позволяет применять закрытые роторы со сравнительно редкой очисткой.

Центрифугальное осветление применяется обычно для обра­ботки тонких и коллоидных суспензий и осуществляется в высокоскоростных центрифугах двумя способами: тонкослойным и   толстослойным.
Тонкослойное центрифугальное осветление отличается от тол­стослойного тем, что в роторе центрифуги поток жидкости делится, с помощью пакета конических тарелок, на слои толщиной не больше 1 мм.Это сокращает продолжительность осаждения частиц и повышает эффективность процесса.

Отстойное центрифугирование является более грубым процессом разделения суспензий, содержащих значительное количество твердой фазы. Для этого требуются роторы большой емкости или приспособления для удаления осадка во время работы центрифуги. При отстойном центрифугировании взаимодействие частиц загрязнения ускоряет процесс их осаждения. В этом случае скорость осаждения определяется более сложным методом, приведен­ным в специальной литературе.

 Центрифугирования масла за один проход через ротор

Вследствие того, что загрязняющие примеси в гидроприводах промышленного оборудования являются высокодисперсными а их концентрация в масле состав­ляет не более 1—2%, процессы очистки, протекающие в роторе центрифуги, относятся к процессам центрифугального осветления.

Так как фактор разделения в обычных промышленных фильтрующих центри­фугах относительно невелик, а частицы имеют высокую степень дисперсности и осаждаются в жидкости высокой вязкости (масло), скорость осаждения частиц, как правило, соответствует закону Стокса

В правильности этого нетрудно убедиться. Например: средний радиус ротора rср = 50 мм, число оборотов ротора п = 6000 об/мин и вязкость масла при температуре 75 0С = 0,22 П, максимальные эквивалентные диаметры частиц загрязнения при которых осаждение будет протекать по закону Стокса составят:

dmax= 120 мк   при    D = 0,3 г/см3   (органические  про­дукты загрязне­ния);
dmax =   58 мк   при    D= 2,6 г/см3 (неорганические продукты загряз­нения);
dmax =   42 мк   при    D = 6,9 г/см3 (железо).

При расчете процессов центробежной очистки масла условно принимается, что весь поток масла в роторе движется без про­скальзывания,  параллельно его оси.

Тогда средняя скорость потока масла в роторе:

где Q — количество масла, проходящее через ротор в единицу времени; R— радиус внутренней поверхности ротора (при заполне­нии ротора осадком — радиус внутренней поверхности осадка); r0— внутренний радиус слоя жидкости в роторе (средний радиус колонки ротора, а при ее отсутствии радиус оси  ротора).

Время пребывания масла в центробежном поле ротора:

где h- средняя   высота  ротора; W = ph (R2 — r02)- рабочий объем   ротора.

Закон Стокса в дифференциальной форме примет вид:

Разделим переменные, получим
   где

Найдем радиус rцилиндрической поверхности, определяющий зону центрифугируемого масла, из которой за время t происходит полное осаждение частиц. Интегрируя левую часть равенства в пределах от r - радиуса указан­ной условной поверхности до R - радиуса   внутренней поверхности ротора, а правую от 0 до t, и решая   получен­ное равенство относительно r, имеем:

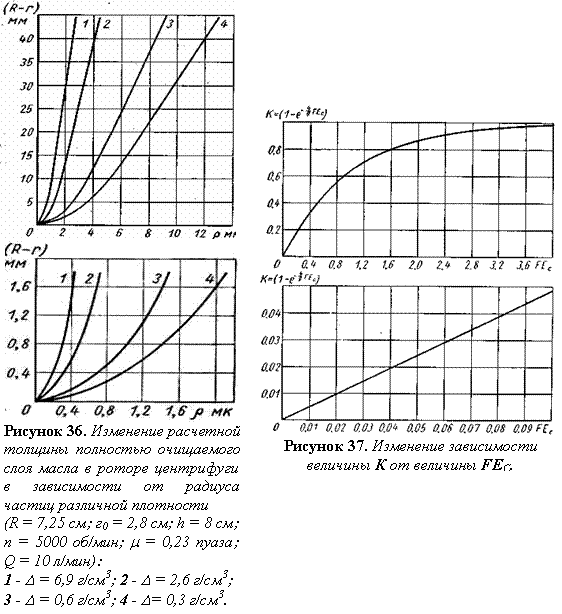
Тогда толщина кольцевого слоя масла, из которого полностью выделяются частицы на стенки ротора, составит (рис. 36):

Из данного уравнения можно найти время, в течение которого стенки ротора достигнут все частицы, находящиеся в начальный момент поступления рабочей жидкости в ротор на расстоянии от оси,  превосходящем r:

Для осаждения всех частиц из всего поступающего в ротор масла (при r = r0) необходимое время пребывания масла в центро­бежном поле можно определить по формуле:

Полнота очистки масла за один проход опреде­ляется коэффициентом очистки:

где х— количество загрязняющих примесей в масле на входе в центрифугу в  %  (по весу); хф— количество загрязняющих примесей в масле на выходе из ротора центрифуги (в % по весу).

Коэффициент j можно также выразить отношением сечения зоны потока, из которого полностью выделяются частицы загряз­нения, к площади полного сечения потока масла в роторе:
   или  
Вводя соответственно F = w2t  и   ,  имеем:

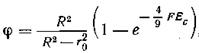
где F— разделяющий  фактор; Ес— разделяемость   смеси.

Произведение разделяющего фактора на разделяемость смеси составит:

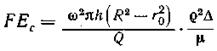
Для определения коэффициента очистки j  при проведении практических расчетов целесообразно использовать равенство:

где  

По справочной кривой (рис. 37) для данного значения FECопределяют значение К,после чего, определяют коэффициент очистки масла j.

В обычных реактивных промышленных фильтрующих центрифугах для основной массы частиц загрязнения (r < 1 мкм)величина j обычно не превышает 0,01, а толщина слоя масла R- r, из которого полностью выделяются частицы загрязнения, не превышает 0,5 мм. Следовательно, в роторе центрифуги в основном происходит тонкослой­ное   центрифугирование   масла.

Предельный радиус частиц, полностью осаждающихся за один проход масла через ротор:
   или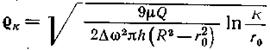  

При практических расчетах можно допустить, что при полном осаждении частиц в роторе скорость их осаждения постоянна и равна средней скорости, соответствующей среднему радиусу положения частицы в жидкости. Тогда время  осаждения частицы:

Необходимым условием для полного осаждения частиц в роторе является
,   или   ,   или 
где Fr ср  - средний фактор  разделения.

Согласно  равенствам:
   и  
где    v0 — скорость  осаждения   частиц  в  гравитационном  поле; vcр - средняя   скорость   осаждения   частиц   в   центробежном   поле, получим:

Левая часть этого уравнения характеризует способность центрифуги полностью очищать (осветлять) масло и называется числом осветления:

Условие полной очистки масла за один его проход через ротор принимает  вид:

Согласно закону Стокса:

Подставляя v0 = Вв уравнение, получаем значение предельного радиуса частиц, пол­ностью осаждающихся   в   роторе:
   или  

В табл. 6 приведены определенные опытным и расчетным путем: предельные радиусы частиц, полностью осаждающихся в роторе центрифуги за один проход масла (R= 7,25 см;r0= 2,8 см;h= 8 см; п = 5000 об/мин; Q = 10 л/мини m = 0,22 П).

Количество примесей, осевших в роторе за один проход через него масла, определим по формуле:

где  0,01хgW - количество примесей в масле, находящемся в  роторе; х— количество загрязняющих примесей в масле на входе в центрифугу в % (по весу); g — плотность суспензии; W— рабочий объем ротора.

Подставив значение , получим:

Количество примесей, осевших в роторе за время t, составит:
 или .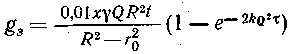

Дифференцируя уравнение по времени, получаем скорость выделения загрязняющих примесей из масла в роторе центрифуги:

Таким образом, коэффициент очистки j служит для каче­ственной оценки полноты процесса центрифугирования в роторе центрифуги. Количественная оценка центрифугирования (скорость выделения в роторе загрязняющих примесей) определяется произведением Qj, которое характеризует интенсивность очисткимасла. Величина Qj представляет собой долю общего потока масла (проходящего через ротор центрифуги в единицу времени), которая подвергается в роторе полной очистке от имеющихся в масле примесей. Поток масла, не подвергающийся очистке, определяется величиной Q(1-j).

Раскрывая значение j  и t, получаем:

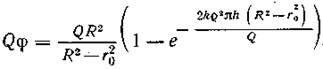
Таким образом, с увеличением расхода Q интенсивность очистки масла и скорость выделения загрязняющих примесей из масла должны повышаться.

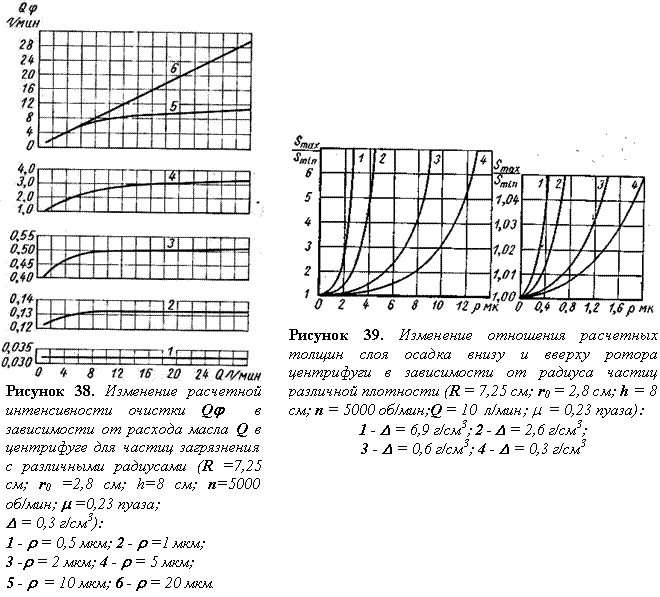
Из расчетных кривых (рис. 38)видно, что в центрифуге интен­сивность очистки масла с увеличением  Qпо мере уменьшения радиуса частиц замедляется и для r <0,5 мкм при D=0,3г/см3 интенсивность очистки практи­чески не зависит от Q.

Влияние увеличения расхода Q на интенсивность очистки масла может происходить только до определенных пределов, после чего повышение расхода Qне только не увеличивает интенсивность очистки, но может привести к значительному ее снижению. Это обусловливается явлением уноса частиц маслом. Сущность этого явления заключается в том, что частицы загрязнения, достигая под действием центробежного поля внутренней стенки ротора, начинают отставать от общего потока масла, и возникающее при этом лобовое воздействие потока на частицу вызывает ее движение по ложу. При этом подъемная сила, обра­зующаяся от наталкивания частицы на неровности ложа, и вихревое движение масла могут перевести частицу обратно во взвешенное состояние.

Критическая   скорость   потока масла в роторе   и критический    расход    его,   соответствующие    началу   уноса   частиц маслом, по В. И. Соколову, соответственно составляют:

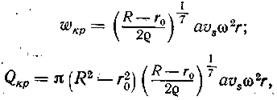
где   R— радиус ложа (внутренний радиус ротора, а при запол­нении  ротора  осадком — внутренний  радиус  осадка); а— коэффициент,    характеризующий    движение    частицы по ложу; vs— скорость осаждения частицы в гравитационном поле. Коэффициент, характеризующий движение частиц:

где   f — коэффициент трения; a — коэффициент   пропорциональности.

Для шарообразных твердых тел можно принять f = 0,666;   a = 0,34, тогда а = 5,37?10-2.

Действительные значения критической скорости и критического расхода значительно выше расчетных, полученных при а = 5,37?10-2. Это объясняется тем, что частицы загрязняющих примесей в масле имеют не сферическую форму, способствующую их уносу со стенок ротора, а произвольную — вплоть до пластинчатой. При этом частицы смолистых продуктов загрязнения прилипают к ложу ротора и друг к другу и создают в роторе вязкий и липкий осадок. Поэтому действительная критическая скорость потока масла в роторе составляет значительную величину 2,5—5 см/сек.

Следует учесть, что центрифугированием не могут быть удалены все высокодисперсные частицы. Существует так называемый предел центрифугирования, характеризующийся критическим размером частицы, ниже которого осаждение частиц в роторе не про­исходит, как бы длительно ни продолжался процесс центрифугирования.

Физическая сущность предела центрифугирования обуслов­лена тем, что скопление высокодисперсных частиц у ограничивающей их движение поверхности ложа при определенных условиях и не стесненном броуновском движении может привести к равен­ству движущей силы процесса и градиента осмотического давления. Предел центрифугирования (сепарации) может быть определён следующей формулой:

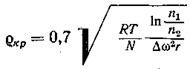
где     R— универсальная  газовая  постоянная; Т — абсолютная   температура; N— число Авогадро; n1 и n2 - соответственно максимальная и минимальная концентрации в   «придонном слое»; D — разность  плотностей дисперсной фазы  и диспер­сионной среды; w — угловая скорость ротора; r— внутренний радиус ротора (радиус ложа).

По данным некоторых исследователей Ln( n1 / n2)=13,8. В этом случае:

В литературе имеются указания о несколько завышенном расчетном значении предельного радиуса частиц в сравнении с действительным  в  трубчатых   центрифугах.

Для экспериментальной центрифуги (r =72,5 мм;  п = 5000 об/мин; m=0,23 пуаза) предельные   размеры   частиц согласно этому уравнению составляют:

Найдем соотношение количеств загрязняющих примесей, осевших в роторе по его высоте за время t:

Дифференцируя по h, получим:

Это уравнение свидетельствует о том, что количество осадка, приходящегося на единицу высоты ротора, уменьшается по высоте, т. е. толщина слоя осадка постепенно уменьшается от нижней части ротора к верхней. При  h= 0 получим:

Исходя из того, что в конце рабочей высоты ротора должны полностью выделиться частицы из внутреннего слоя суспензии радиуса r, найдем рабочую высоту ротора:

Подставляя это значение hв предыдущее уравнение, получаем
                     

Принимая с некоторым приближением, что количество осадка, приходящегося на единицу высоты ротора, прямо пропорцио­нально толщине слоя осадка, получим:

где Smax - толщина слоя осадка внизу ротора; Smin - толщина слоя осадка вверху ротора (рис. 39).

Частицы загрязняющих примесей имеют различные величины r и D (полидисперсная система). Для упрощения расчетов полидисперсная система с различ­ными значениями Dприводится к полидисперсной системе с одним приведенным значением Dлр. При этом значения приведенных эквивалентных радиусов  частиц можно  получить  из равенства:

При   полидисперсной   системе   коэффициент   очистки   масла в  роторе:

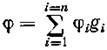
где ji - коэффициент очистки  масла в роторе от частиц радиуса ri; gi = xi/x – «относительное»количество частиц в загрязняющих примесях с радиусом ri; п - количество эквивалентных радиусов различных частиц. Раскрывая правую часть уравнения, получим:

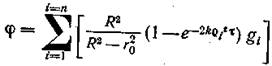
При полидисперсной системе отношение максимального и мини­мального количеств осадка загрязняющих примесей на единице высоты ротора, составит: