СОДЕРЖАНИЕ РАБОТЫ
-
Получить задание по одному из вариантов таблицы
-
Подготовить нечеткие правила в соответствии с графическим представлением функций задания. Трехмерное изображение выбранной зависимости построить, воспользовавшись программными средствами MATLAB. При этом можно руководствоваться программой нижеприведенного примера, которая моделирует зависимость 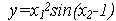 % Построение графика функции y=x1^2*sin(x2-1)
% Построение графика функции y=x1^2*sin(x2-1)
% в области x1 =[-6, 4],x2=[-4.4, 1.7].
n=15; %количество точек дискретизации
x1=linspace(-6, 4, n); x2=linspace(-4.4, 1.7, n);
y=zeros(n, n);for j=1:n
y(j,:)=x1.^2*sin(x2(j)-1);end
surf(x1, x2, y)
xlabel('x_1'); ylabel('x_2'); zlabel('y');
title('Искомая зависимость')
Можно воспользоваться и возможностями пакета Symbolic Math Toolbox, введя, например, следующие команды:
syms x y %создаем символьные переменные
z=x^2*sin(y-1);
ezsurf(z,[-2,2])
Сформируем нечеткие правила, соответствующие зависимости выходной переменной от входных по полученной поверхности рис. 1.
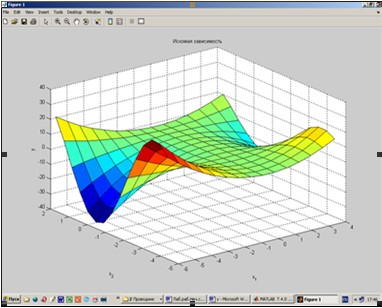
Рис. 1. Графическое представление функции 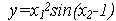
Для лингвистической оценки входных переменных х1 и х2 выберем по три терма - низкий, средний, высокий; для выходной y пять термов - низкий, ниже среднего, средний, выше среднего, высокий. Получим, например, следующие правила:
- ЕСЛИ х1= низкий И х2= низкий, ТО y= высокий;
- ЕСЛИ х1= низкий И х2= средний, ТО y= низкий;
- ЕСЛИ х1= низкий И х2= высокий, ТО y= высокий;
- ЕСЛИ х1= средний, ТО y= средний;
- ЕСЛИ х1= высокий И х2= низкий, ТО y= выше среднего;
- ЕСЛИ х1=высокий И х2= средний, ТО y= ниже среднего;
- ЕСЛИ х1= высокий И х2=высокий, ТО y= выше среднего.
-
Спроектировать нечеткую систему, выполнив следующую последовательность шагов.
Шаг 1. Открыть FIS–редактор, напечатав слово fuzzy в командной строке.
Шаг 2. В появившемся графическом окне FIS Editor добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.
Шаг 3. Переименуем первую входную переменную. Для этого сделаем щелчок левой кнопкой мыши на блоке input1, введем новое обозначение х1 в поле редактирования имени текущей переменной и нажмем <Enter>.
Шаг 4. Переименуем вторую входную переменную, введя х2 на блоке input2.
Шаг 5. Переименуем выходную переменную. Для этого щелкнем мышкой на блоке output1. Введем новое обозначение у в поле редактирования имени текущей переменной; нажмем <Enter>.
Шаг 6. Зададим имя системы. Для этого в меню File выберем в подменю Export команду To File… и введем имя файла, например, ivanov 1.
Шаг 7. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1 и зададим диапазон изменения переменной 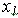 , напечатав -6 4 в поле Range (рис. 2). , напечатав -6 4 в поле Range (рис. 2).
Шаг 8. Зададим функции принадлежности переменной 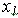 . Для лингвистической оценки этой переменной будем использовать три терма с треугольными функциями принадлежности. Эти функции установлены по умолчанию, поэтому переходим к следующему шагу. . Для лингвистической оценки этой переменной будем использовать три терма с треугольными функциями принадлежности. Эти функции установлены по умолчанию, поэтому переходим к следующему шагу.
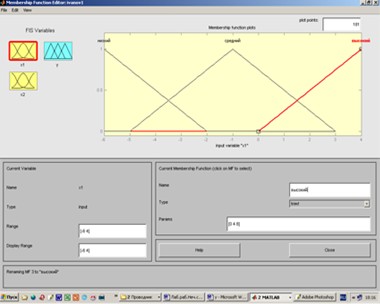
Рис. 2. Функции принадлежности переменной 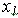
Шаг 9. Зададим наименования термов переменной х1. Для этого щелкнем мышкой по графику первой функции принадлежности (см. рис. 2). График активной функции принадлежности выделяется красной жирной линией. Затем введем наименование терма Низкий в поле Name и нажмем <Enter>. Щелкнем мышкой по графику второй функции принадлежности, введем наименование терма Средний в поле Name и нажмем <Enter>. Щелкнем мышкой по графику третьей функции принадлежности, введем наименование терма Высокий в поле Name и нажмем <Enter>.
Шаг 10. Зададим функции принадлежности переменной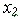 . Для этого активизируем переменную . Для этого активизируем переменную 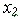 щелчком мышкой по блоку х2. Зададим диапазон изменения переменной х2. Для этого напечатаем -4.4 1.7 в поле Range и нажмем <Enter>. Для лингвистической оценки этой переменной будем использовать как и ранее три терма с треугольными функциями принадлежности. Они установлены по умолчанию, поэтому переходим к следующему шагу. щелчком мышкой по блоку х2. Зададим диапазон изменения переменной х2. Для этого напечатаем -4.4 1.7 в поле Range и нажмем <Enter>. Для лингвистической оценки этой переменной будем использовать как и ранее три терма с треугольными функциями принадлежности. Они установлены по умолчанию, поэтому переходим к следующему шагу.
Шаг 11. По аналогии с шагом 9 зададим следующие наименования термов переменной х2: Низкий, Средний, Высокий.
Шаг 12. Зададим функции принадлежности переменной у. Для лингвистической оценки этой переменной будем использовать пять термов с гауссовыми функциями принадлежности. Для этого щелчком мыши по блоку у активизируем переменную у. Зададим диапазон изменения переменной у. Для этого напечатаем -50 50 в поле Range(рис. 3) и нажмем <Enter>. Затем в меню Edit выберем команду Remove All MFs для удаления установленных по умолчанию функций принадлежности. После этого в меню Edit выберем команду Add MFs… В появившемся диалоговом окне выберем тип функции принадлежности gaussmf в поле МF tуре и пять термов в поле Number МFs. После ввода функций принадлежности редактор активизирует первую входную переменную, поэтому для продолжения работы щелкнем мышкой по пиктограмме у.
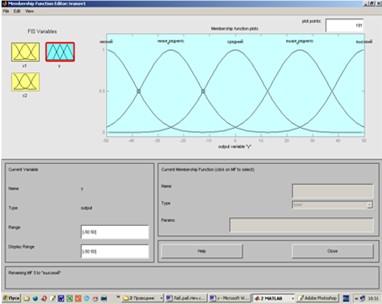
Рис.3. Функции принадлежности переменной у.
Шаг 13. По аналогии с шагом 9 зададим следующие наименования термов переменной у: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рис. 3.
Шаг 14. Перейдем в редактор базы знаний Rule Editor. Для этого в меню Edit выберем команду Rules... Для ввода правила выбираем в меню соответствующую комбинацию термов и нажимаем кнопку Add rule. На рис. 4 изображено окно редактора базы знаний после ввода всех семи правил. В конце правил в скобках указаны весовые коэффициенты.
Шаг 15. Сохраним созданную систему. Для этого в меню File выберем в подменю Ехроrt команду То File.
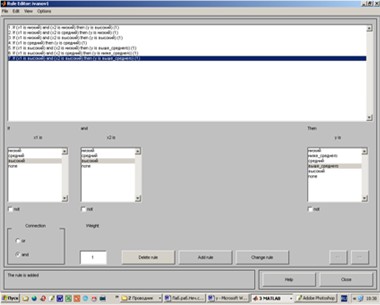
Рис.4.Нечеткая база знаний Мамдани
На рис. 5 приведено окно визуализации нечеткого вывода. Окно активизируется командой Rules меню View. В поле Input указываются значения входных переменных, для которых выполняется нечеткий логический вывод.
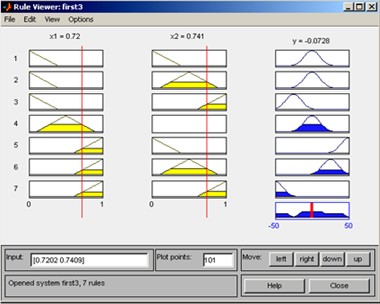
Рис. 5. Визуализация нечеткого вывода Мамдани
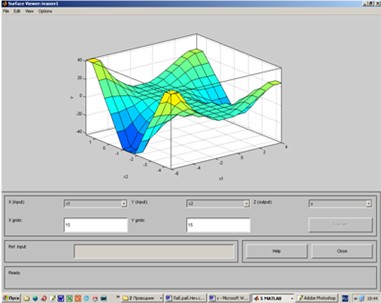
Рис. 6. Поверхность «входы - выход» для базы знаний в Surface Viewer
На рис. 6 приведена поверхность «входы - выход», соответствующая синте¬ированной нечеткой системе. Окно выводится по команде Surface меню View.
При сравнении поверхностей на рис. 1 и 6 можно сделать выводы относительно качества описания нечеткими правилами моделируемой нелинейной зависимости.
|
|
