Методические указания к практическим занятиям по курсу "Микропроцессорная техника"

Цель работы: Изучение основ синтеза комбинационных логических устройств на произвольных логических элементах.

Сложные логические функции могут быть построены путем последовательного выполнения функциональных зависимостей, связывающих пары переменных.

Если число аргументов логической функции равно 2, то число функций равно 16. Имея элементы, осуществляющие элементарные логические операции, можно выполнить любую сложную логическую операцию.

Такую систему функций можно назвать полный системой или базисом. Однако, условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных логических функций, является условием, достаточным для синтеза логического устройства любой сложности, но это условие не является необходимым, т.е. при синтезе можно ограничиться меньшим набором элементарных логических функций.

Последовательно исключая из базиса функции, можно полечить так называемый минимальный базис. Под минимальным базисом понимают такой набор функций, исключение из которого любой функции превращает этот набор в неполную систему функций.

Возможны различные минимальные базисы, отличающиеся числом входящих в них функций и видов этих функций. Выбор того или иного базиса для синтеза логического устройства связан с тем, насколько просто, удобно и экономично можно выполнить элементы, реализующие элементарные функции, которые входят в выбранный базис, и в целом все логическое устройство.

Наиболее часто синтез логических устройств производиться с использованием базисов:
- И, ИЛИ, НЕ;
- И-НЕ;
- ИЛИ-НЕ.

Два последних базиса в настоящее время в связи с широким использование интегральных логических элементов при построении логических устройств приобрели важное значение.

Синтез логического устройства распадается на несколько этапов.

На первом этапе требуется функцию, заданную в словесной, табличной или других формах, представить в виде логического выражения с использованием некоторого базиса. Дальнейшие этапы сводятся к получению минимальных форм функций, обеспечивающих при синтезе наименьшее количество электронного оборудования и рациональное построение функциональной схемы логического устройства.

Исходными, из соображений удобства последующих преобразований, приняты следующие две канонические формы представления функций: Совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).

Дадим ряд определений /1/.

Введем обозначение

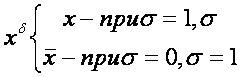
Определение 1. Формула , где  - какой-либо двоичный набор, а среди переменных Х_i могут быть совпадающие, называется элементарной конъюнкцией.

Определение 2. Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой(сокращенно ДНФ).

Примером ДНФ может служить выражение:

Приведем форму представления функции, не являющейся ДНФ. Например, функция  представлена не в форме ДНФ, так как последний член не является элементарной конъюнкцией аргументов.

Определение 3. Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождение под знаком отрицания).

Определение 4. Правильная элементарная конъюнкция называется полной относительно переменных х₁,…,х_n, если в нее каждая из этих переменных входит один и только один раз (быть может под знаком отрицания).

Определение 5. Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных х₁,…,х_n называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных x₁,…,x_n

Примером СДНФ может служить выражение:

                 (1)

Если исходная функция дана в табличном форме, то СДНФ может быть получена непосредственно.

Для функции (1) таблица истинности имеет вид:

Как видно из выражения для y, в нем каждый член соответствует определенному набору значений аргументов, при котором функция равна 1. Таких наборов 4 (столбцы 3,4,6,8). На этих наборах вся функция оказывается равной 1. Комбинации переменных, при которых у=1, называется конституентами единицы или минтермами.

Сформулируем правило записи СДНФ функции, заданной таблицей истинности.

Необходимо записать столько членов в виде конъюнкции всех аргументов, сколько единиц содержит функция в таблице истинности. Каждая функция должна соответствовать определенному набору аргументов, образующих функцию в 1, а если в этом наборе значение аргумента равно 0, то в конъюнкцию входит инверсия данного аргумента.

Дадим аналогичные определения для СКНФ.

Определение 6. Формула называется элементарной дизъюнкцией.

Определение 7. Всякая конъюнкция элементарных дизъюнкций называется конъюнктивной нормально формой (КНФ).

Примером КНФ может служить выражение

Приведем функцию, не являющуюся КНФ:

Здесь третий член не является элементарной дизъюнкцией аргументов (или их инверсий).

Определение 8. Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождение под знаком отрицания).

Определение 9. Правильная элементарная конъюнкция называется полной относительно переменных x₁,…,x_n, если каждая из этих переменных входит в нее один и только один раз (быть может, под знаком отрицания).

Определение 10. Совершенной конъюнктивной нормальной формой (СКНФ) относительно переменных x₁,…,x_n называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильны и полны относительно переменных x₁,…,x_n.

СКНФ функции легко строится по таблице истинности. Сформулируем правило записи СКНФ функции, заданной таблицей истинности.

Следует записать столько конъюнктивных членов, представляющих собой дизъюнкции всех аргументов, при скольких наборах значении аргументов функция равна 0, и если в наборах значений аргумента равна 1, то в дизъюнкцию входит инверсия этого аргумента.

Каждый сомножитель в СКНФ состоит из суммы аргументов, для которых функция обращается в ноль в соответствии с таблицей истинности. Комбинации переменных, при которых у=0, называют конституентами нули или макстермами.

СКНФ функции, приведенной в таблице, построенная в соответствии с правилом, имеет вид:

              (2)

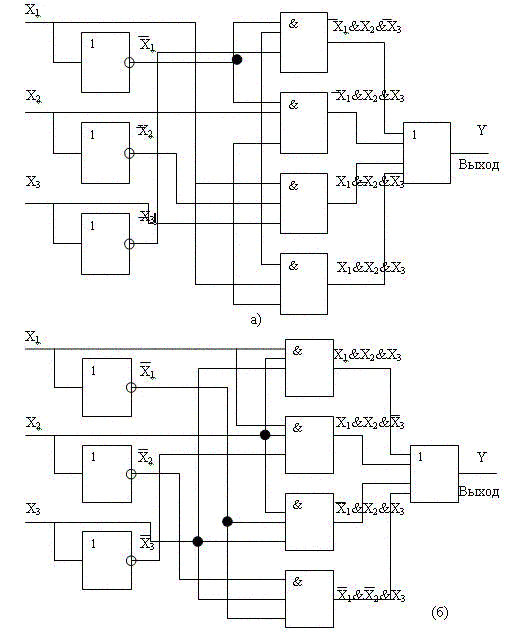
Рисунок 1. Схемы устройств, построенных по СДНФ (а) и СКНФ (б).

Функциональная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Получающиеся при этом схемы для функций (1) и (2) приведены на рисунке 1.

Недостаток такого метода построения схем логических устройств состоит в том, что получающиеся схемы, как правило, оказываются неоправданно сложными, требуют использования большого числа логических элементов.

Во многих случаях удается так упростить логическое выражение, не нарушая функции, чтобы соответствующая схема логического устройства оказалась существенно более простой. Методы такого упрощения функции называются методами минимизации функций алгебры логики.

ЗАДАНИЯ

Для логических функций, заданных в таблице, выполнить задания п.п. 1-9.

1.     Представить функцию у₁ в СДНФ

2.     Представить функцию у₁ в СКНФ

3.     Представить функцию у₂ в СДНФ

4.     Представить функцию у₂ в СКНФ

5.     Представить функцию у₃ в СДНФ

6.     Представить функцию у₃ в СКНФ

7.     Представить функцию у₄ в СДНФ

8.     Представить функцию у₄ в СКНФ

9.     Составьте функциональные схемы логических устройств, реализующих функции п.п. 1-8 задания.

Литература

1.     Гиндикин С.Г. Алгебра логики в задачах. – М.: Наука, 1972,286 с.

2.      Микроэлектронные устройства автоматики.: Учебн. Пособие для вузов / А.А. Сазонов, А.Ю. Лукичев, В.Т. Николаев и др.; Под ред. А.А. Сзанова. – М.: Энергоатомиздат, 1991. – 384с.