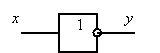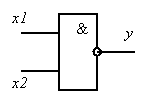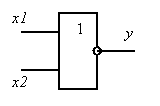Методические указания к практическим занятиям по курсу "Микропроцессорная техника"
Цель работы: Изучение основных законов алгебры логики, классификации устройств цифровой техники, типовых логических элементов и математических основ синтеза логических устройств.
1. Понятие о логической функции и логическом устройстве
Для обозначения различных понятий, предметов, действий пользуются словами. Слова строятся из букв, которые берутся из некоторого набора, называемого алфавитом.
В цифровой технике для этих же целей пользуются кодовыми словами (обычно одинаковой длины), для построения которых применяют простейший алфавит, состоящий лишь из двух букв. Эти буквы принято обозначать символами 0 и 1. Таким образом, в цифровой технике кодовое олово – это последовательность символов 0 и 1 определенной длины, например, 01011101. Такими словами могут представляться и числа, в этом случае 0 и 1 совпадает по смыслу с обычными арабскими цифрами. При представлении кодовым словом некоторой нечисловой информации, чтобы отличить буквы 0 и 1 от цифр, будем эти буквы называть соответственно логическим нулем и логической единицей.
Если длина кодовых слов составляет n разрядов, то можно построить 2п различных комбинации – кодовых слов. Например, при п = 3 можно построить 23 = 8 кодовых слов или входных наборов: 000, 001, 010, 011, 100, 101, 110, 111.
Информация, которая передается между отдельными узлами (блоками) сложного цифрового устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла поступают кодовые слова, а на выходе узла образуется новое кодовое слово, представляющее собой результат обработки входных кодовых слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Для того чтобы подчеркнуть отличительную особенность таких функций, состоящую в том, что сама функция и ее аргументы могут принимать значения логических 0 и 1, будем эти функции называть функциями алгебры логики (булевыми функциями). Следовательно, булева функция – это двоичная функция двоичных аргументов.
Устройства, предназначенные для формирования и реализации функций алгебры логики, в дальнейшем будем называть логическими или цифровыми устройствами. По функциональному назначению цифровые устройства подразделяют на элементы: логические, хранения информация (элементы памяти), вспомогательные и специальные.
Цифровые устройства (либо их узлы) можно делить на типы по разным признакам.
По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.
На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно: символ за символом (в так называемой последовательной форме). В такой последовательной форме формируется и выходное слово. Пример такого устройства показан на рисунке 1.lа.
На входы устройства параллельного действия все n символов каждого входного кодового слова подаются одновременно (в так называемой параллельной форме). В такой же форме образуется выходное слово. Очевидно, при параллельной форме приема и выдачи кодовых слов в логическом устройстве необходимо иметь для каждого разряда входного (выходного) слова отдельный вход (выход).
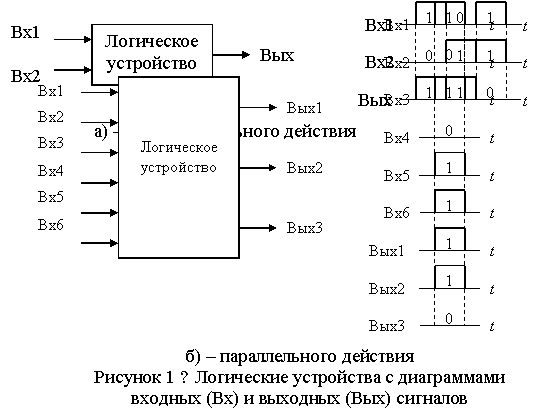 |
Пример такого устройства показан на рисунке 1.1б. Устройство выполняет над разрядами входных слов ту же логическую операцию (выявляя несовпадение символов соответствующих разрядов входных слов) что и устройство, показанное на рисунке 1.1а, но в параллельной форме. Входы устройства разделены на две группы: Вх1, Вх2, Вх3, Вх4, Вх5, Вх6, каждая из которых предназначена для приема трехразрядного входного кодового слова в параллельной форме. На выходах устройства также в параллельной форме получается трехразрядное выходное кодовое слово.
В устройствах смешанного действия входные и выходные кодовые слова представляются в разных формах. Например, входные слова в последовательной форме, а выходные – в параллельной. Устройства смешанного действия могут использоваться
использоваться для преобразования кодовых слов из одной формы представления в другую (из последовательной формы в параллельную и наоборот).
По типу схемного построения логические устройства (и их схемы) делят на два класса: комбинационные устройства (и, соответственно, комбинационные схемы) и последовательностные устройства (последовательностные схемы).
В комбинационном устройстве (называемом также автоматом без памяти) каждым символ на выходе (логический 0 или логическая 1) определяется лишь символами (логический 0 или логическая 1), действующими в данный момент времени на входах устройства, и не зависит от того, какие символы ранее действовали на этих входах. В этом смысле комбинационные устройства лишены памяти (они не хранят сведения о прошлом работы устройства).
В последовательностных устройствах (или автоматах с памятью) выходной сигнал определяется не только набором символов, действующих в данный момент времени на входах, но и внутренним состоянием устройства. Последнее зависит от того, какие наборы символов действовали в предшествующие моменты времени. Из-за этого свойства устройство находится в одном из возможных состояний (в зависимости от символов, действовавших на входах в предшествующие моменты времени), и можно говорить, что последовательностные устройства обладают памятью (они хранят информация о прошлом состоянии устройства).
Рассмотрим примеры комбинационного и последовательностного устройств.
Пусть устройство (рисунок 1а) предназначено для формирования на выходе сигнала, определяющего совпадение сигналов на входах. На выходе формируется логическая 1 в случаях, когда на обоих входах действует логическая 1 либо логический 0: если на одном из входов действует логическая 1, а на другом – логический 0, тo на выходе устройства формируется логический 0, Такое устройство представляет собой пример комбинационного устройства, в котором значение формируемой на выходе логической функции определяется лишь значениями аргументов в данный момент времени.
Рассмотрим другой пример. Счетчик на рисунок 1б подсчитывает импульсы. В каждый момент времени его состояние соответствует числу поступивших на вход импульсов. Выходная информация определяется тем, каково было состояние счетчика до данного момента времени и поступает
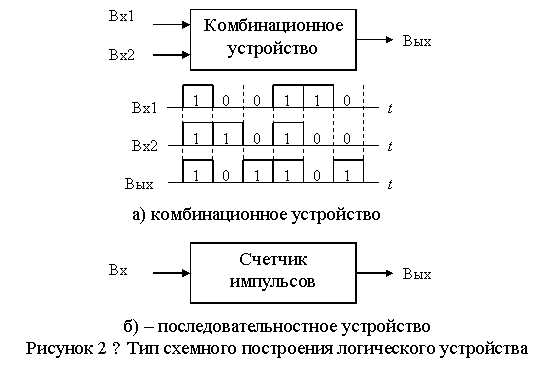 |
или нет на вход импульс в этот момент. Таким образом, данное устройство является последователностным устройством.
Последовательностные устройства подразделяются еще на два вида: синхронные и асинхронные. В синхронных устройствах цепи обратной связи содержат элементы задержки. Они управляется внешними тактовыми сигналами и выполняют функцию запоминания сигналов внутренних переменных на один такт.
В асинхронных устройствах задержка сигналов внутренних переменных обусловлена только инерционностью логических элементов.
2 Элементарные логические функции
В математике для задания функции обычно используются два способа: аналитический и табличный. Подобными же способами могут задаваться логические функции /1/.
При использовании табличного способа строится так называемая таблица истинности, в которой приводится все возможные сочетания значений аргументов и соответствующие им значения логической функции.
Аналитический способ задания логической функции предусматривает запись функции в виде логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.
В дальнейшем функции одного и двух аргументов будем называть элементарными логическими функциями, имея в виду, что логические выражения этих функций, содержащие не более одной логической операции, элементарны.
В таблице 1 приведены основные элементарные логические функции.
Таблица 1 – Элементарные логические функции
|
Название логической функции |
Логическое выражение |
Таблица истинности |
Условное обозначение логического элемента |
|||
|
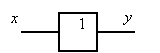
Повторение |
|
x y 0 0 1 1
|
БУФЕР
|
|||
|
Инверсия |
|
x y 0 1 1 0
|
НЕ
|
|||
|
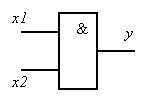
Конъюнкция |
|
x1 x2 y 0 0 0 1 0 0 0 1 0 1 1 1 |
|
|||
|
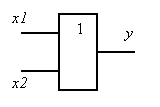
Дезъюнкция |
|
x1 x2 y 0 0 0 1 0 1 0 1 1 1 1 1 |
|
|||
|
Штрих Шефера |
|
x1 x2 y 0 0 1 1 0 1 0 1 1 1 1 0 |
|
|||
|
Стрелка Пирса |
|
x1 x2 y 0 0 1 1 0 0 0 1 0 1 1 0 |
|
|||
|
Неравнозначность |
|
x1 x2 y 0 0 0 1 0 1 0 1 1 1 1 0 |
|
Рассмотрим особенности работы логических элементов, реализующих элементарные логические функции.
БУФЕР не изменяет логического состояния цифрового сигнала. Буферы обычно применяются для повышения нагрузочной способности по току, а также нормирования логических уровней в устройствах сопряжения (интерфейсах).
Элемент НЕ (инвертор) осуществляет дополнение логического состояния, т.е. логическая 1 на входе вызывает логический 0 на выходе и наоборот. Кроме того, инверторы усиливают сигнал по току и как буферы применяются в схемах интерфейсов.
На выходе элемента И логическая 1 появляется, если только все входы одновременно находятся в состоянии логической 1. Все остальные комбинации логических сигналов (уровней) приводят к образованию на выходе логического 0.
На выходе элемента ИЛИ появляется логическая 1, если хотя бы один из входов находится в состоянии логической 1. Выход элемента ИЛИ соответствует логическому 0, если состояния всех входов одновременно равны логическому 0.
На выходе элемента И-НЕ образуется логический 0, когда все входы одновременно находятся в состоянии логической 1. Любая другая комбинация входов вызывает появление на выходе логической 1. Следовательно, элемент И-НЕ – это элемент И с инвертированным выходом, что отражено на графическом обозначении элемента И-НЕ кружком со стороны выхода.
На выходе элемента ИЛИ-НЕ появляется логическая 1, если только все его входы одновременно находятся в состоянии логического 0. Любая другая комбинация входов вызывает появление на выходе логического 0.
Элемент ИЛИ-НЕ – это элемент ИЛИ с инвертированный выходом, что отражено на его графической обозначении кружком со стороны выхода.
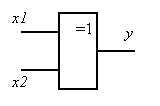
Выход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ (сумматор по модулю 2) соответствует логической 1, если один из входов находится в состоянии логической единицы, а другой – в состоянии логического 0. На выходе появляется логический 0, когда логические состояния обоих входов одинаковы.
Использование дополнительного инвертора позволяет
реализовать инверсию функции неравнозначности и получить выполнение функции
равнозначности: ![]()
К элементарным логическим функциям относится функция
(операция) запрета: ![]() .
Эта функция имеет значение логической 1, если на входе х1, (основной
вход) воздействует сигнал логической 1, а на запрещающем входе х2 –
сигнал логического 0.
.
Эта функция имеет значение логической 1, если на входе х1, (основной
вход) воздействует сигнал логической 1, а на запрещающем входе х2 –
сигнал логического 0.
Основой синтеза логических устройств являются аксиомы, тождества и законы алгебры логики /3/;
Аксиомы:
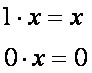
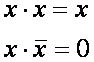
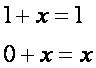
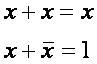
Тождества:
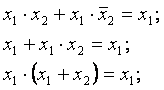
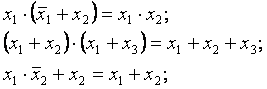
Законы:
- сочетательный
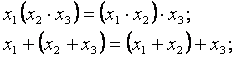
- переместительный

- распределительный
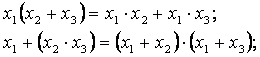
- формулы де Моргана
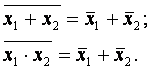
Сформулируем следующее правило применения формул де Моргана к сложным логическим выражениям.
Инверсия любого сложного выражения, в котором аргументы (либо их инверсии) связаны операциями конъюнкции и дизъюнкции, может быть представлена тем же выражением с изменением всех знаков конъюнкции на знаки дизъюнкции, знаков дизъюнкции на знаки конъюнкции и инверсии всех аргументов.
ЗАДАНИЕ
1. Упростите логические функции, используя аксиомы и тождества алгебры логики:

2. Докажите тождества алгебры логики:
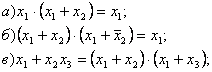
3. Используя таблицы истинности, докажите тождества алгебры логики.
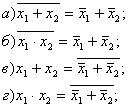
4. Используя законы алгебры логики, упростите логическое выражение:
![]()
5.
Упростите логические выражения:

6. Покажите, что:
а) операция конъюнкции (И) представима через операции дизъюнкции (ИЛИ) и инверсии (НЕ);
б) операция дизъюнкции (ИЛИ) представима через операции конъюнкции (И) и инверсии (НЕ).
7. Выразите операцию конъюнкцию ЗАПРЕТ.
8. Пользуясь формулой да Моргана, преобразуйте следующие логические выражения:
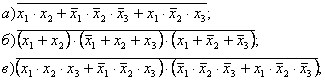
9.
Покажите, что, если ![]() то
то
![]() .
.
10. Составьте схемы логических устройств, реализующих следующие логические функции:
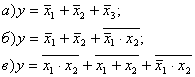
Литература
1. Лобанов В.И. Азбука разработчика цифровых устройств. – М.: Горячая линия – Телеком, 2001. 192 с.: ил. – (Массовая радиобиблиотека; 1247).
2. Микроэлектронные устройства автоматики: Учеб. пособие для вузов/ А.А. Сазонов, А.Ю. Лукичев. В.Т. Николаев и др. Под ред. А.А. Сазонова. – М.: Энергоатомиздат, 1991. 384 с.: ил.
3. Калабеков Б.А. Цифровые устройства и многопроцессорные системы: Учебник для техникумов связи. – М.: Горячая линия – Телеком, 2003. 336 с.: ил.
4. Гусев В.Г. Электроника и микропроцессорная техника: Учеб. для вузов/ В.Г. Гусев, Ю.М. Гусев. – 3–е изд., перераб. и доп. – М.: высш. шк., 2004. – 790 с.: ил.