Рассмотренные в предыдущем параграфе методы анализа нелинейных систем относятся к таким системам, у которых в системе дифференциальных уравнений удается выделить несколько уравнений, в которых перед производными стоит «большой» параметр. Именно в этом случае имеется возможность построить иерархию взаимосвязанных дифференциальных уравнений по принципу «медленности» времени.

В отличие от системы (2.12) здесь рассматриваются системы, имеющие малый параметр не при производных, а перед нелинейной функцией. Такие системы называются квазилинейными [14, 15]. Кроме этого рассматриваются системы, состоящие из уравнений второго порядка. Это связано с тем, что при составлении дифференциальных уравнений используются методы Лагранжа или Гамильтона. Нелинейные же функции, зависящие от координат и их производных, вводятся в систему прямым образом. Примером такой системы является следующее скалярное уравнение Ван-дер-Поля

Именно для этого уравнения голландским инженером Ван-дер-Полем предложен метод построения решений, который в дальнейшем был развит Н.М.Крыловым, Н.Н.Боголюбовым и Ю.А. Митропольским. Ими были предложены и доказаны не только условия сходимости решений в виде асимптотических разложений для системы общего виде (2.13), но и рассмотрены различные случае, в том числе и случай неавтономной системы, системы, в которой рассматриваются медленные изменения внешнего возмущения и пр.

Принимая во внимание эти обстоятельства, Н.М. Крыловым и Н.Н. Боголюбовым предложено решение (2.13) искать в виде следующего асимптотического разложения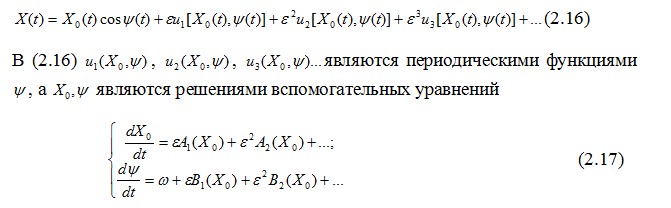

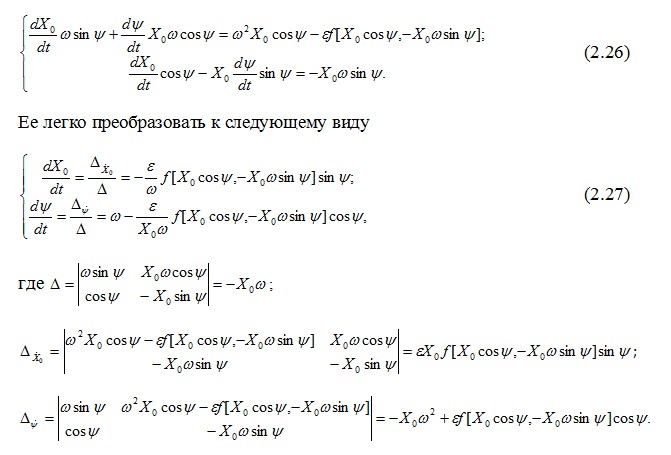
В нелинейной динамике уравнения (2.28) называются укороченными или уравнениями Ван-дер-Поля. Они во своему виду напоминают две составляющих эквивалентной передаточной функции нелинейного элемента в методе гармонической линеаризации. Однако в отличие от метода гармонической линеаризации с помощь. (2.28) можно анализировать не стационарное состояние, а переходные процессы. Н.М. Крыловым и Н.Н. Боголюбовым показано, что уравнения (2.28) соответствуют тем, которые получаются по первому приближению исходя из разработанной ими теории асимптотических методов анализа нелинейных систем.

Анализируя состояние разработанных методов анализа нелинейных систем, необходимо отметить, что эти методы применимы лишь для анализа одночастотных процессов, в том числе для определения автоколебаний. При анализе двухчастотных процессом (двумерных инвариантных торов) эти методы становятся настолько громоздкими, что практически не используются в практике анализа конкретных систем. При анализе хаотических (странных) аттракторов они не применимы в принципе. Кроме этого эти методы рассматривают квазилинейные системы, то есть системы, в которых при нелинейной функции имеется возможность установить малый параметр. В связи с развитием вычислительной техники для анализа нелинейных систем в настоящее время большее распространение получили методы прямого интегрирования уравнений динамики. Однако все приближенные методы интегрирования имеют большой недостаток, заключающийся в том, что нет возможности анализа и оценки точности получаемых результатов. Это относится особенно к тем случаям, когда система обладает большой чувствительностью к вариациям параметров и начальных условий.