С середины шестидесятых годов прошлого столетия стала динамично развиваться теория оптимального управления. Действительно очень заманчиво разработать математический аппарат, с помощью которого удалось бы синтезировать систему управления, наилучшую в каком – то смысле. В становление теории оптимального управления большой вклад внести выдающиеся математики нашей страны и мира. В частности Л.С. Понтрягин, А.М. Летов, Красовский Н.Н., Красовский А.А., Р. Беллман, Л. Маркус и др.

Здесь, прежде всего, стали рассматриваться случаи, когда математическое описание систем определяется следующими детерминированными дифференциальными уравнениями

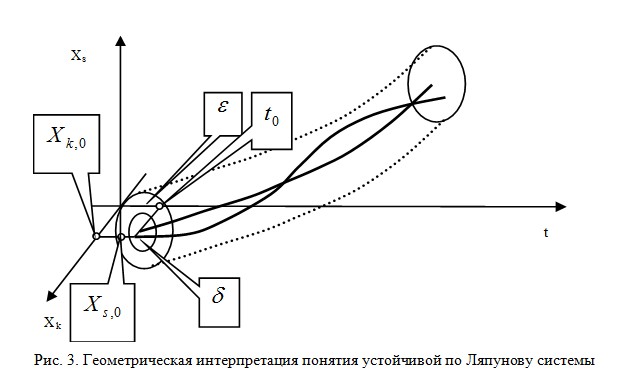
Современная постановка проблемы устойчивости принадлежит А.М. Ляпунову, опубликованная в его фундаментальной работе: «Общая задача устойчивости движения». (Ляпунов А.М. Общая задача устойчивости движения. – М.: ОНТИ, 1935). Необходимо отметить, что понятие устойчивости и сформулированные и доказанные основные теоремы имеют фундаментальный характер и они справедливы и в настоящее время. Они справедливы для линейных и нелинейных систем, для систем с постоянными и (или) переменными параметрами. Здесь ограничимся случаем автономной системы, динамика которой описывается системой

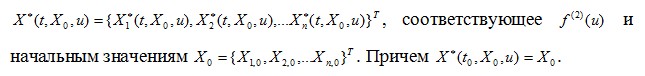
В этом случае для анализа устойчивости необходимо использовать теорию Флоке. Рассмотрение этой теории не входит в задачу этого курса. Обычно в традиционных инженерных курсах в вузах теорию Флоке не рассматривают. Для таки систем, характерно, например, параметрическое возбуждение колебаний и другие эффекты. Для интересующихся студентов можно ее изучить, например, по учебнику: Данжело г. Линейные системы с переменными параметрами. М.: Машиностроение, 1974. Здесь отметим, что устойчивые периодические траектории формируют притягивающее многообразие в пространстве состояния. Поэтому они называются инвариантными многообразиями. Притягивающее многообразие типа предельного цикла называются автоколебаниями.

Во многих практических задачах приходиться иметь дело с траекториями, периодически изменяющимися с несколькими периодами. Например, рассматривается траектория, состоящая из двух гармонических колебаний с двумя частотами. В пространстве состояния такие траектории формируют тор. Если два периода (частоты), то такой тор будет двумерным. Если такой тор характеризует притягивающее многообразие, то он является двумерным инвариантным тором. Теория устойчивости для торов уже не разработана. Выяснение условий формирования в пространстве состояния инвариантных торов уже является очень сложной задачей, решение которой является скорее искусством. Мы видим, что уже анализ устойчивости достаточно простых траекторий в пространстве состояния представляет не решенную до настоящего времени проблему.

3) Траектория есть некоторая не периодическая функция времени. Здесь исчерпывающе рассмотрены только некоторые частные случаи. Многие вопросы, имеющие чисто математическую формулировку для этого случая решены. Большой вклад в формулирование и доказательство некоторых вопросов теории внесли А. Андронов, Р. Беллман, А. Пуанкаре и др. С основными положениями этих теорий можно познакомиться в учебнике Демидович Б.П. Лекции по математической теории устойчивости.М.: Наука, 1967.- 469 с.

Обобщая приведенный материал, можно заметить, что теория устойчивости систем автоматического управления в настоящее время разработана полностью для линейных систем с постоянными и периодическими параметрами, когда параметры имеют один период повторения. Для нелинейных систем в общем случае можно пользоваться вторым методом Ляпунова на основе построения функции Ляпунова. Оценка устойчивости может быть выполнена также и на основе применения показателей Ляпунова. Однако реальное использование этих методов вызывает сложности при рассмотрении конкретной системы.