СИНТЕЗ ДИСКРЕТНЫХ АВТОМАТОВ

2. СИНТЕЗ ДИСКРЕТНЫХ АВТОМАТОВ

2.1. Основные положения двоичной алгебры.

Отношения между двумя элементами определяются отношением экви­валентности, обозначаемым знаком равенства, и операциями: сложения (дизъюнкции), обозначаемой знаками <+> или <> ,умножения (конъюнкции) — < • > или < > и отрицания (инверсии) —

При выполнении всех трех операций отношения эквивалентности определяются следующими выражениями:

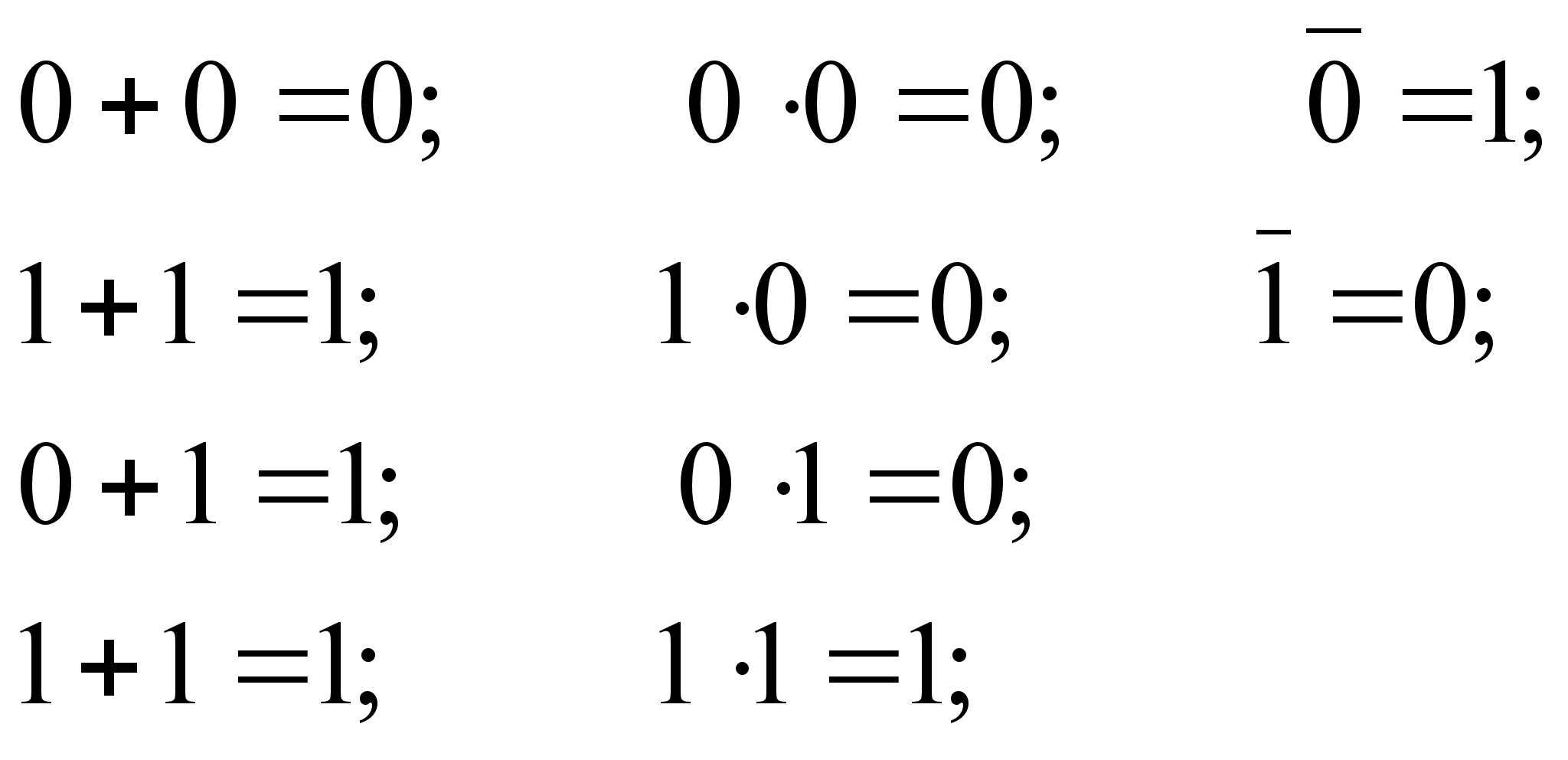
Эти постулаты позволяют обосновать законы двоичной алгебры. Законы одинарных элементов: универсального множества:

х + 1 = 1; х 1 =х;

нулевого множества:

х + 0 = х; х • 0 = 0.

Законы отрицания (теорема Моргана):

двойного отрицания:

дополнительности:

двойственности:

Законы комбинационные:

тавтологии: x + х = х; х х = х;

коммутативные или переместительные: x1+x2=x2+x1 x1x2=x2x1

ассоциативные или согласовательные:

(х1 + х2) + х3 = x1+ (x2 + х3); (х1 х2) х3 = x1 (x2 х3);

дистрибутивные или распределительные:

х1 (х2 + х3 )= x1x2 + x1 х3; х1 + (х2 х3)= (х1 + х2) + (x2 + х3);

абсорбции или поглощения: х1 + x1x2 = x1; х1 + (x1+x2 )= x1;

склеивания: x1x2 + x1 = x1

2.2. Синтез комбинационных автоматов

Для создания сложных комбинационных автоматов используют элементарные комбинационные автоматы (логические элементы), которыми реализуется функционально полный набор двоичных функций. Элементарным комбинационным автоматом будем называть автомат, реализующий логическую функцию двух переменных.

Синтез комбинационных автоматов начинается с содержательного описания функционирования объекта и составления таблицы истин­ности.

Для получения аналитического выражения, определяющего необходимую структуру автомата, записываются исходные формы переключательной функции в виде совершенной дизъюнктивной (СДНФ) или конъюнктивной (СКНФ) нормальной формы.

Дизъюнктивная нормальная форма представляет собой дизъюнкцию (сумму) минтермов, а СКНФ — конъюнкцию (произведение) макстермов.

Минтермом или конституэнтой единицы называется логическая функция, принимающая значение 1 только на одном наборе перемен­ных. Образуется как конъюнкция всех входных переменных с отрица­нием тех, которые в данном наборе равны нулю. Число минтермов рав­но числу наборов.

Макстермом или конституэнтой нуля называется логическая функция, принимающая значение 0 только на одном наборе переменных. Образуется как дизъюнкция входных переменных, где переменные данного набора, равные 1, взяты с отрицанием. Число макстермов равно числу наборов.

Две эти формы эквивалентны. При минимизации удобно пользоваться СДНФ.

Рассмотрим методы синтеза автоматов с минимальным количест­вом элементов, которые называются минимальными или оптималь­ными.

Пример. Разработать автомат, реагирующий не менее чем на два сигнала из трех (мажоритарный автомат).

Таблица 3

Таблица истинности автомата

x1

0

1

0

1

0

1

0

1

x2

0

0

1

1

0

0

1

1

x3

0

0

0

0

1

1

1

1

y

0

0

0

1

0

1

1

1


1. По таблице истинности записывается логическая функция в форме СДНФ. Число слагаемых равно числу наборов, где синтезируемая функция равна 1, а число сомножителей в каждом слагаемом — числу аргументов. Над аргументами, принимающими в данном наборе значение 0, ставится знак отрицания:

2. Минимизация СДНФ. Производится наиболее популярным (табличным) методом Куайн-Мак Ласки. (существуют также методы Карно, Квайна [2]).

    1. Анализируем таблицу истинности:

Таблица 4.


№

строки

x1

x2

x3

y

Минтерм

Кол-во единиц

1

0

0

0

0



2

1

0

0

0



3

0

1

0

0



4

1

1

0

1

2

5

0

0

1

0



6

1

0

1

1

2

7

0

1

1

1

2

8

1

1

1

1

3

2.2 Группируем минтермы по количеству в них единиц

Таблица 5.

№

группы

№

строки

x1

x2

x3

Кол-во единиц

1

4

1

1

0

2

1

6

1

0

1

2

1

7

0

1

1

2

2

8

1

1

1

3

    1. Произведем объединение строк каждых предыдущих и последующих групп. Объединяются строки, в которых какой либо X различается значением (0 или 1) – смежные минтермы. Такой Х обозначаем “+”

Таблица 6.

№№

строк

x1

x2

x3

Кол-во

единиц

4, 8

1

1

+

2

6, 8

1

+

1

2

7, 8

+

1

1

2

2.4. Производится объединение строк с совпадающими позициями «+». В нашем примере таких нет.

2.5. Из двух строк с совпадающими позициями “+” оставляем только одну.

Приведенный выше алгоритм минимизации СДНФ позволяет получить следующую логическую функцию автомата:

y = x1x2+x1x3+x2x3

3. Двукратное инвертирование СДНФ (переход в базис Шеффера).

4. Построение логической схемы автомата.













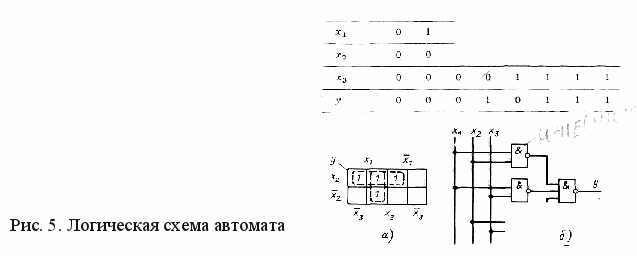
2.3. Синтез последовательностных автоматов.

Последовательностные автоматы осуществляют преобразование двоичных входных переменных не только с учетом текущей комбинации на входе в данном такте автоматного времени, но и с учетом того, что было в предыдущих тактах.

Создание последовательностного автомата, способного запоминать предшествующие данному такту комбинации сигналов на входе, обеспечивается наличием в комбинационном автомате не только внешних (рабочих) входов X и выходов Y, но и вспомогательных (внутренних) переменных Z, которые должны иметь возможность давать различные комбинации для каждого такта, подлежащего запоминанию, и реализуемых в виде обратных связей. Эти внутренние переменные, подаваемые на вход комбинационной схемы, как бы корректируют результат от воздействия внешних входов, учитывая предыдущие ситуации.

Таким образом, задача внешних входов — задать текущую комбинацию, а внутренних — сохранить и задать на входе комбинацию, однозначно соответствующую сформировавшейся на выходе в предыдущем такте (кодирующую ее). В этом случае выходная комбинация формируется с учетом предыдущего такта. В следующем такте внутренние переменные внесут очередную коррективу (если их комбинация будет отлична от предыдущей) и, следовательно, новые значения выходов уже несут в себе следы двух предыдущих тактов и т.д. Количество таких состояний М внутренних переменных Z называется весом последовательностного автомата.

Число внутренних переменных mz, обеспечивающих возможность кодирования всех М состояний, называется объемом памяти автомата и равно

mz = log2M.

Внешними входными переменными автомата определяется количество его возможных входных комбинаций, а внутренними — через сколько комбинаций внешних начинает повторяться коррекция внутренними. Так, если тх = 3 и mz = 2, то автомат будет иметь восемь состояний с повторяющейся коррекцией через четыре такта.

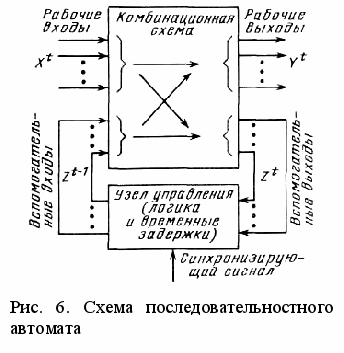
Следствием этого является характерная особенность последовательностных автоматов: у них вследствие коррекции Z возможны разные комбинации выходов при одинаковых комбинациях на внешних входах. Технических вариантов реализации даже простых последовательностных автоматов может быть очень много. Достаточно наглядной является схема последовательностных автоматов, приведенная на рис. 6 и представляющая собой наиболее общий случай.

Входы X t логикой комбинационной схемы формируют выходы Y t в данном такте. В формировании Y t при этом участвуют внутренние переменные Z t-1 , комбинация которых сформировалась в предыдущем такте t-1. Переменные Z t-1 сформировались узлом управления ОС в цепи обратной связи, который может включать: комбинационную логику, временные задержки и синхронизующий вход. Как видно из схемы, именно ОС обеспечивает "запоминание" путем приема на вход выходной комбинации автомата в данном такте и передачу ее с временной задержкой на входы автомата в следующем такте.

Разрыв цепи ОС превращает последовательностные автоматы в комбинационные. Важную роль играет характер задержки: если блок ОС имеет синхронизирующий вход, "отпирающий" и "запирающий" цепь обратной связи в каждом такте, — это синхронный автомат. У него равенство

Z t-1=Z t наступает только после "отпирания" синхроимпульсом цепи обратной связи.

Благодаря обратной связи последовательностные автоматы обладают специфическим свойством, характерным для замкнутых систем управления — они могут быть устойчивыми и неустойчивыми. Устойчивым будем называть состояние, когда комбинация выходов меняется лишь вследствие изменения входа. Неустойчивые автоматы могут после установления комбинации входов несколько раз менять комбинацию на выходе, проходя ряд неустойчивых состояний. Такой процесс может завершиться переходом в устойчивое состояние (затухание колебаний) либо продол­жаться неограниченное время (автоколебания).

Рассмотрим этапы более общего синтеза последовательностного автомата, у которого переход из одного состояния в другое зависит не только от прихода очередного тактового импульса, но и от условий, сформированных "внешней" логикой -- различными датчиками и внешними управляющими командами.

Этап 1. Составим описание цикла функционирования механизма или агрегата, для автоматизации которого разрабатывается автомат. Установим количество состояний (тактов), когда не меняются состояние ни одного дискретного исполнительного элемента, составляющее цикл работы механизма, и причины перехода из одного состояния в другое.

В зависимости от причин может меняться последовательность смены состояний, но не их номенклатура. Под причинами понимается срабатывание какого-либо датчика или командного органа либо изменение какого-либо сочетания их состояний. Например, в описании цикла установлено, что цикл состоит из пяти тактов (состояний а1 . . а5), переходы которых обусловлены различными сочетаниями команд оператора х1 — х3 и сигналов датчиков z1 — z4 (см. рис. 7, а).

















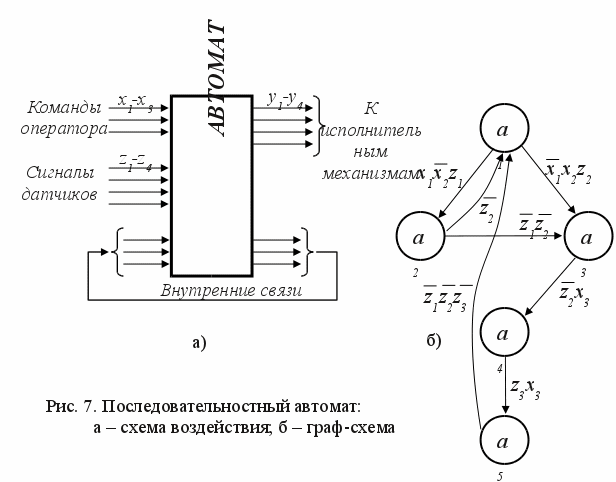
Этап 2. Составим формальный портрет, отражающий все реально возможные переходы из одного состояния в другое и условия этих переходов. Он может быть составлен в виде тактовой таблицы, структурной схемы алгоритма или в виде графа, вершинами которого являются состояния, а ребра отражают причины перехода из одного состояния в другое. Над ребрами записаны логические условия перехода. На рис. 7, б показан возможный вариант такого графа.

Этап 3. Произведем кодирование состояний. Чтобы автомат "знал" какое в данном такте состояние, он должен иметь узел, на выходах которого появляется 1 в зависимости от состояния, а именно: на первом - при a1, на втором - при а2 и т.д. Таким узлом может быть дешифратор с тремя триггерами на входе. При кодировании состояний каждому состоянию ставится в соответствие комбинация состояний выходов триггеров.

Чтобы закодировать пять состояний, нужны три триггера с выходами Q0.Q1.Q2:

Таблица 7

Состояние

Q0

Q1

Q2

а1

0

0

1

а2

0

1

0

а3

0

1

1

а4

1

0

0

а5

1

0

1

Не используются еще три возможных состояния 3-х триггеров (23= 8)

Этап 4. Составим таблицу переходов, в которой на основании графа отразим переход каждого выхода каждого триггера при всех возможных переходах автомата из одного состояния в другое. В этой же таблице укажем логические условия каждого перехода и состояние входов JK каждого триггера при известном переходе его выхода, характерные только для выбранного JK-триггера.

Таблица 8.

Исходное состояние

Код исходного состояния

Новое состояние

Код нового состояния

Условия

перехода

Состояние входов триг­геров*

J0

K0

J1

K1

J2

К2

а1

001

а2

010

X1X2’Z1

~

1

1

~

0

~

а3

011

X1’X2Z2

~

0

1

~

0

~

а2

010

а1

011

Z1’

1

~

~

1

0

~

а3

011

Z1’Z2’

1

~

~

0

0

~

а3

011

а4

100

Z2’X3

~

1

~

1

1

~

а4

100

а5

101

Z3X3

1

~

0

~

~

0

а5

101

а1

001

Z1’Z2’Z3

~

0

0

~

~

1

* Работа JK-триггера определяется следующей таблицей состояний:


J

K

Qn+1

/Qn+1

0

0

Qn

/Qn

1

0

1

0

0

1

0

1

1

1

/Qn

Qn

Этап 5. По таблице перехода запишем логические уравнения, связывающие входы триггеров с командными входами х сигналами датчиков z и выходами триггеров Q через дешифратор состояний. Запись уравне­ний производится следующим образом: для каждого входа каждого триггера для переходов, где данный вход равен 1, записывается произведение исходного состояния на логическое условие его перехода в последующее. Уравнения имеют вид




















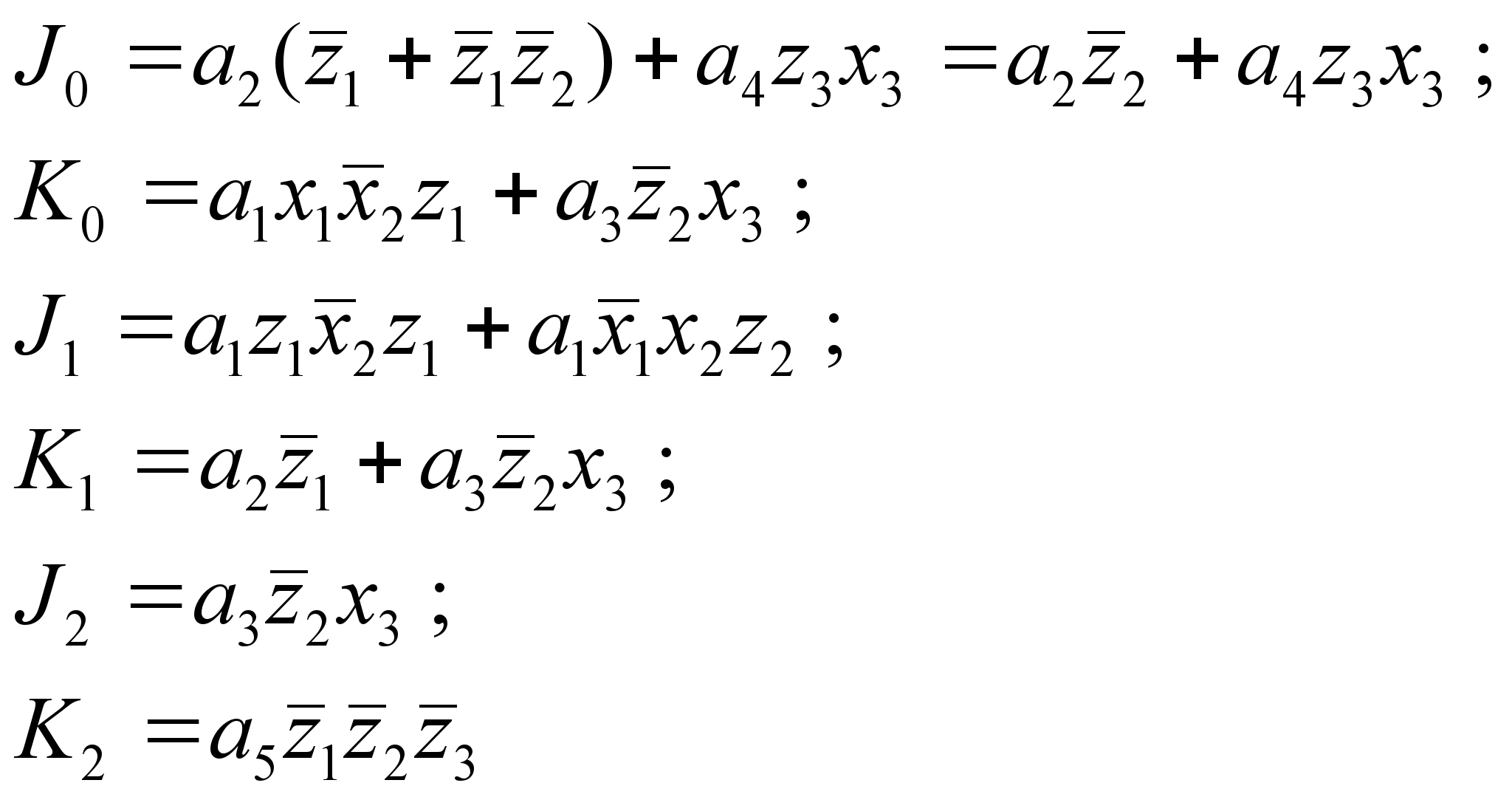
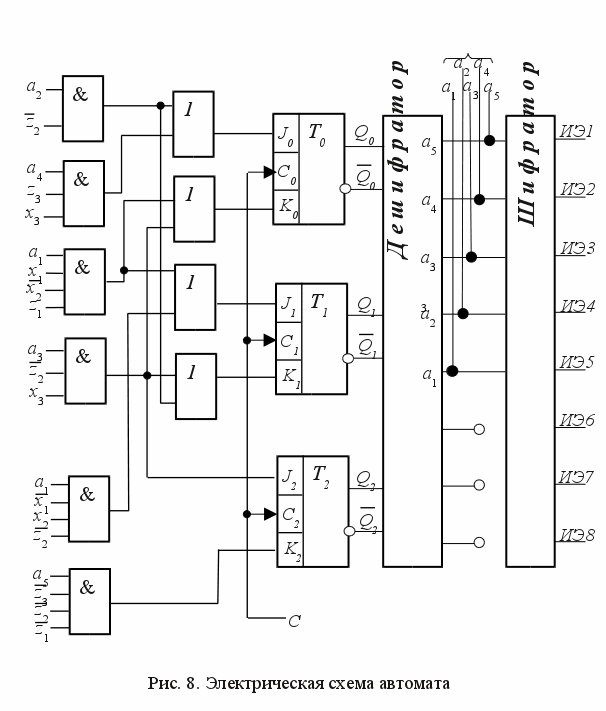
Полученный автомат (рис. 8) может обеспечить пятитактовый цикл управления какими-либо исполнительными элементами. Их не может быть менее трех (чтобы получилось пять разных состояний), но больше может быть (10, 20 и т.п.), т.е. каждое состояние будет отличаться комбинацией включенных и отключенных элементов (станков, механизмов).