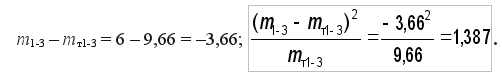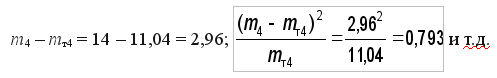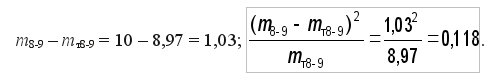В теории вероятностей применяют несколько критериев согласия. Применительно к показателям надежности тракторов и сельскохозяйственных машин чаще всего используют критерий согласия Пирсона Χ2. Критерий согласия Пирсона Χ2 представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале статистического ряда информации:
где nу – число интервалов в укрупненном статистическом ряду;
Теоретическую частоту можно определить по формуле (16) или
где N — количество точек информации; F(tiк) и F(tiн) — интегральные функции соответственно в конце и начале i-го интервала значений показателя надежности. Если исходная информация о показателе надежности представлена в виде статистического ряда, то для определения критерия согласия Χ2 составляют укрупненный статистический ряд, соблюдая правило: nу ≥ 4, mi ≥ 5. При этом допускается объединение тех интервалов, в которых mi < 5. Укрупним крайние интервалы (слева и справа) для которых mi ≥ 5, объединяя рядом расположенные интервалы. Из оценки эмпирических частот mi (табл. 3) следует, что необходимо объединить интервалы 1 — 3 (mi = 2). Тогда m1-3 = 2 + 2 + 2 = 6; аналогично объединим интервалы 8 и 9, так как m8 = 4 m8-9 = 4 + 6 = 10. Число укрупненных интервалов nу = 6 и их результаты занесем в табл. 4 и 5 (см. нижнюю часть таблиц). Соответственно объединим и теоретические вероятности для этих интервалов. Для нормального закона распределения (НЗР) теоретическая вероятность на этих интервалах:
Рассчитаем критерий согласия Пирсона Χ2по формуле (21) для конца первого укрупненного интервала статистического ряда
Для конца четвертого интервала
Для конца укрупненного 8 – 9 интервала
Результаты расчета сведены в табл. 4. ТЗР выбирают по величине критерия Χ2 [уравнение (21)] и по данным табл. 4: Пользуясь критерием согласия Χ2, по табл. VIII приложения определяют вероятность совпадения опытных и теоретических данных. Вероятность совпадения при прочих равных условиях зависит и от повторности использованной информации. Поэтому для входа в табл. VIII приложения необходимо определить число степеней свободы r по уравнению: r = n – К – 1, (22) где n — число интервалов статистического ряда (nу = 6);
Для закона нормального распределения: К = 2 ( r = 6 – 2 – 1 = 3, тогда по табл. VIII приложения Χ2табл = 3,67, что соответствует вероятности совпадения Р = 30% или Χ2табл = 4,642 — вероятности совпадения Р = 20%. Χ2табл = 4,642 > 3,755, то вероятности совпадения Р ≈ 27%. Для закона распределения Вейбулла (ЗРВ) теоретическая вероятность на этих интервалах:
Рассчитаем критерий согласия Пирсона Χ2 по формуле (21) для конца первого укрупненного интервала статистического ряда
Для конца четвертого интервала
Для конца укрупненного 8 – 9 интервала
Результаты расчета сведены в табл. 5. ТЗР выбирают по величине критерия Χ2 [уравнение (21)] и по данным табл. 5: Χ2 = 1,387 + 0,793 + 0,5 +…+ 0,118 = 4,174. Число степеней свободы r или номер строки для табл. Х приложения определяется по формуле (22): r = 6 – 3 – 1 = 2, где К = 3 — число параметров для закона распределения Вейбулла (a, b и tсм), если tсм = 0 то К = 2. Тогда по табл. Х приложения Χ2табл = 4,605, что соответствует вероятности совпадения Р = 10% илиΧ2табл = 3,219 – вероятности совпадения Р = 20%. Χ2табл = 4,605 > 4,174, то вероятности совпадения Р ≈ 11%. Таким образом, вероятность совпадения закона нормального распределения (Χ2 = 3,755) составляет около 27% – выше, чем вероятность совпадения закона распределения Вейбулла (Χ2 = 4,174) — около 11%. Следует иметь в виду, что критической вероятностью совпадения принято считать Р = 10%. Если Р < 10%, выбранный для выравнивания теоретический закон распределения следует считать непригодным. |


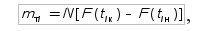
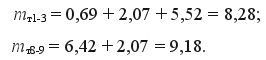
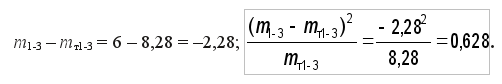
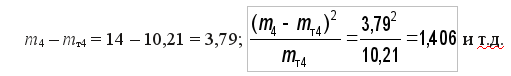
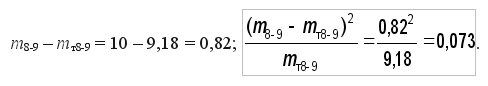
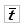 и S),
и S),