При наличии полной информации расчет показателей надежности можно проводить как аналитическим, так и графическим методом на основе дифференциальной или интегральной функции выбранного теоретического закона распределения (ЗНР или ЗРВ). К преимуществам графического метода расчета относится возможность наложения кривых этих функций соответственно на полигон и кривую накопленных опытных вероятностей и на этой основе визуального определения, наиболее совпадающего с опытной информацией теоретического закона распределения (ЗНР или ЗРВ), которым и следует пользоваться при дальнейших расчетах показателей надежности. Известно, что применительно к отказам дифференциальная и интегральная функции характеризуют количество потерявших работоспособность машин или их элементов, или, что практически одно и то же, необходимое количество ремонтных воздействий (устранение эксплуатационных отказов и проведение ремонтов). По дифференциальной функции f(t) удобно определять количество отказов, и соответственно количество ремонтных воздействий в любом интервале наработок, а по интегральной функции — суммарное их количество от начала наблюдения за машинами до заданной наработки t. Для закона нормального распределения (ЗНР) точки дифференциальной кривой определяются по уравнению:
где S – среднее квадратическое отклонение случайной величины ti ;
– центрированная функция закона нормального распределения;
где
Для 1-го интервала: абсцисса — значение показателя надежности в середине первого интервала t1с = Тдр1 = 1750 мото-ч;
величину функции f0(t) можно определить по таблице [3] или рассчитать на микрокалькуляторе по формуле (15):
Следовательно, в интервале наработок от 1500 до 2000 мото-ч выйдет из строя (ресурсный отказ) и потребует ремонта около 1% двигателей. Для 2-го интервала t2с = Тдр2 = 2250 мото-ч;
или для 3% двигателей потребуется ремонт в этом интервале наработок и т. д. (в курсовой работе приводятся все расчеты). Для 9-го интервала t9с = Тдр9 = 5750 мото-ч;
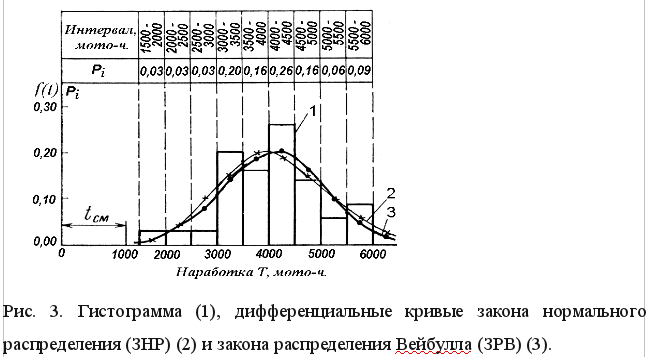
Промежуточные и окончательные результаты расчета приведены в табл. 4. Проверка правильности расчетов осуществляется сложением величин f(t) (∑f(t) ≈ 1), результат заносится в последний столбец табл. 4. По данным расчета построена кривая дифференциальной f(t) функции ЗНР наложенная на гистограмму (рис. 3). Теоретическая частота mтi выхода двигателей из строя определяется по формуле:
где N = 69 — число двигателей (уточненный объём выборки). Результаты расчета приведены в табл. 4. Значения интегральной функции F(t) определяют по уравнению
где tiк — верхняя граница соответствующего интервала.
Для 1-й точки интегральной кривой Tкдр1 = 2000 мото-ч,
Следовательно, в интервале наработок от 0 до 2000 мото-ч выйдет из строя около 1% двигателей. Для 2-й точки интегральной кривой Tкдр2 = 2500 мото-ч,
и так далее (в контрольной работе приводятся все расчеты). Для 9-й точки интегральной кривой Tкдр9 = 6000 мото-ч,
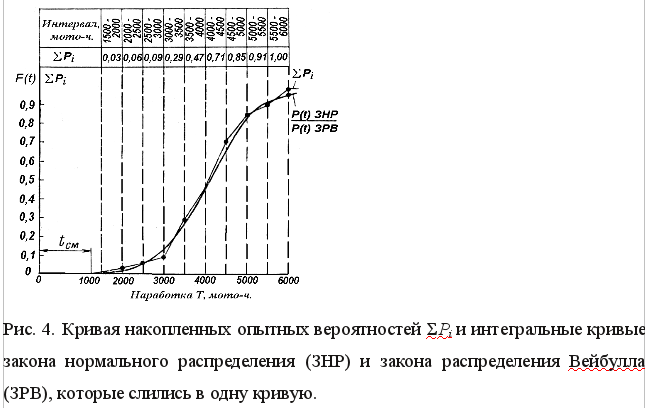
Результаты расчета приведены в табл. 4. По данным расчета построена кривая интегральной F(t) функции ЗНР (рис. 4).
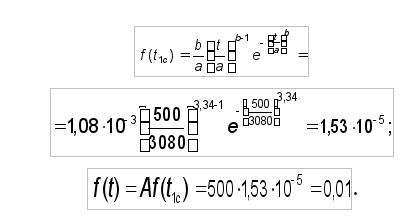
Для закона распределения Вейбулла (ЗРВ) с параметрами: а = 3080 мото-ч., b = 3,34, tсм = 1250 мото-ч. (см. п. 7) точки дифференциальной кривой определяются по уравнению:
где A — величина интервала;
Для 1-го интервала абсцисса — значение показателя надежности в середине первого интервала t1с = Тдр1 = 1750 мото-ч: ордината — значение дифференциальной функции в первом интервале, уравнение (18): t = t1c – tсм = 1750 – 1250 = 500 мото-ч; величину функции f(t1с) можно рассчитать на микрокалькуляторе по формуле (19):
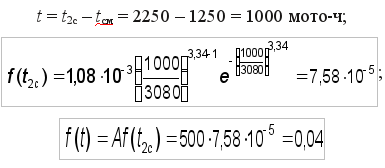
Для 2-го интервала t2с = Тдр2 = 2250 мото-ч;
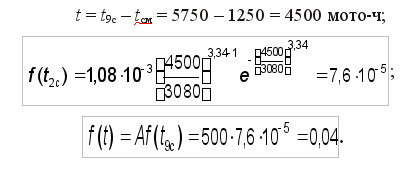
и т. д. (в курсовой работе приводятся все расчеты). Для 9-го интервала t9с = Тдр9 = 5750 мото-ч;
Промежуточные и окончательные результаты расчета приведены в табл. 5. Проверка правильности расчетов осуществляется сложением величин f(t) (∑f(t) 1), результат заносится в последний столбец табл. 5. По данным расчета построена кривая дифференциальной функции ЗРВ f(t) (рис. 3). Теоретическая частота mтi определяется по формуле (16):
где N = 69 – число двигателей (уточненный объём выборки). Результаты расчета приведены в табл. 5. Значения интегральной функции F(t) определяют по уравнению
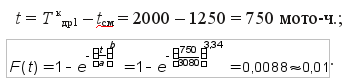
где t = Tкдрi – tсм Для 1-й точки интегральной кривой Tкдр1 = 2000 мото-ч,
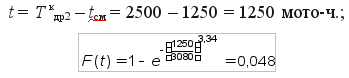
Для 2-й точки интегральной кривой Tкдр2 = 2500 мото-ч,
и так далее (в контрольной работе приводятся все расчеты). Для 9-й точки интегральной кривой Tкдр9 = 6000 мото-ч,
Результаты расчета приведены в табл. 5. По данным расчета построена кривая интегральной функциии ЗВР F(t) (рис. 4). |

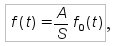 (14)
(14) (15)
(15)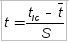 – квантиль нормального распределения,
– квантиль нормального распределения,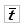 – среднее арифметическое значение (математическое ожидание) случайной величины t.
– среднее арифметическое значение (математическое ожидание) случайной величины t.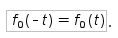
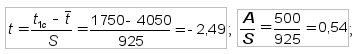



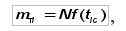 (16)
(16) (17)
(17)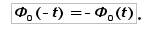



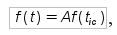 (18)
(18)
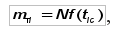
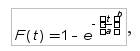 (20)
(20)