

Передний и задний углы для любой точки лезвия сверла Спиральное сверло является специфическим режущим инструментом, у которого передний и задний углы не являются постоянными по длине главных режущих лезвий 1-3 и 2-4 (рис.2.10). Найдем зависимость для определения переднего угла сверла в произвольно расположенной главной секущей плоскости, например, на текущем диаметре Dx (см. рис.2.10). Как следует из рис.2.9, стандартный главный передний угол определяется для периферийной точки 2 главного лезвия 2-4. 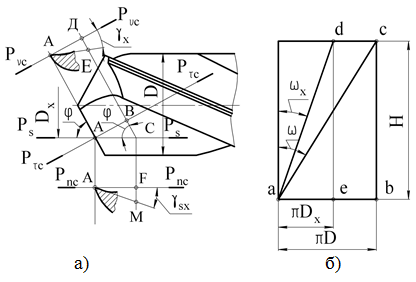 Рис.2.10. Схема для определения переднего угла для любой точки лезвия сверла Просмотр рисунка Возьмем на главном лезвии сверла произвольную точку A и построим сечения главной секущей плоскостью Pτc и рабочей плоскостью Ps , получим передние углы: главный и в продольном сечении Ps - Ps (он не является для сверла стандартным). Из Δ-ка ADE (рис.2.10) следует: 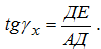 По построению АД = АВ, поэтому 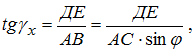 откуда  Аналогично 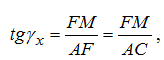 откуда  Примем, что главные лезвия сверла лежат в диаметральной плоскости, т.е. 2α=0 (см. рис.2.9). Для этого случая DE≈FM и, приравнивая правые части в (2.2) и (2.3), получим: 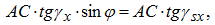 откуда  Передний угол в рабочей плоскости (в продольном сечении) для периферийной точки сверла (см. рис.2.10, а) равен углу наклона винтовой стружечной канавки ω, т.е. γs≡ ω , очевидно, что и γsx≡ ωx . Развернем сверло по диаметру D на длине шага винтовой линии (см. рис.2.10, б). Из треугольников abc и ade имеем: 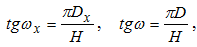 откуда  или  Подставив (2.6) в (2.4), найдем:  Из зависимости (2.7) следует, что передний угол сверла имеет максимальное значение на периферии и к центру сверла уменьшается. Независимо от способа заточки сверл по задней поверхности (плоская, коническая, цилиндрическая или винтовая) задние углы по длине лезвия также переменны, но максимальное значение их будет в точках, лежащих на оси сверла. Для плоской заточки, например, полученная нами формула для определения заднего угла сверла в цилиндрическом сечении имеет вид [6]:  где μx - текущий угол точки на лезвии сверла: ψ≤μx≤ψ0, где tgμ0 =2a/D (рис.2.11). 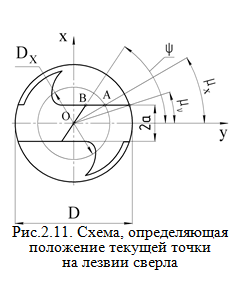
Из формулы (2.8) видно, что задний угол на сверле при плоской заточке зависит от расположения точки на лезвии (угол μx ). Предельным значением μx является угол ψ (см. рис.2.11), поэтому cos(ψ-μx)=1 для точки , и задний угол для нее αB имеет макси-мальное значение. 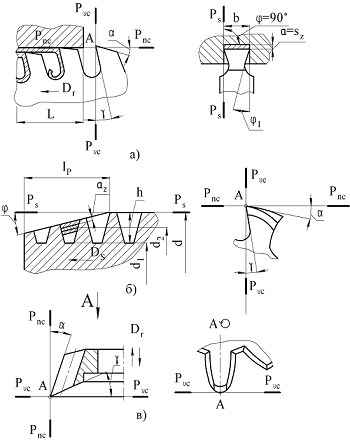 Рис.2.12. Координатные плоскости и углы резания для плоской протяжки (а), метчика (б) и зуборезного долбяка (в) Просмотр рисунка На рис.2.12 в качестве примера показаны координатные плоскости и углы резания других типов инструментов. |
