Геометрия режущих инструментов

Самый простой металлорежущий инструмент – токарный резец – состоит из головки (рабочей части) с режущими кромками и тела, служащего для закрепления в суппорте станка или специальной державке (рис.2.3).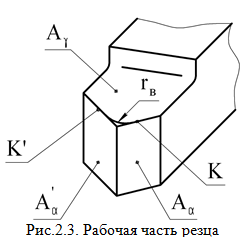

Головка резца ограничена рядом поверхностей:

A_γ- передняя поверхность лезвия (передняя поверхность) - поверхность лезвия инструмента, контактирующая в процессе резания со срезаемым слоем и со стружкой;

- задняя поверхность лезвия (задняя поверхность) – это поверхность лезвия инструмента, контактирующая в процессе резания с поверхностями заготовки;

- режущая кромка – кромка лезвия инструмента, образуемая пересечением передней и задней поверхностей лезвия. Инструмент имеет главную режущую кромку и вспомогательную режущую кромку ;

A_α- главная задняя поверхность - задняя поверхность лезвия инструмента, прилегающая к главной режущей кромке;

A'_α- вспомогательная задняя поверхность - задняя поверхность лезвия инструмента, примыкающая к вспомогательной режущей кромке;

- вершина лезвия (вершина) – участок режущей кромки в месте пересечения двух задних поверхностей;

ρ - радиус округления режущей кромки - радиус кривизны режущей кромки в сечении ее нормальной секущей плоскостью;

r_в- радиус вершины - это радиус кривизны вершины лезвия.

Взаимное расположение указанных поверхностей и режущих кромок в пространстве определяется с помощью ряда углов, составляющих в совокупности геометрию резца. Для определения углов инструмента используются различные системы координатных плоскостей и соответствующие координатные плоскости. Различают инструментальную, статическую и кинематическую системы координатных плоскостей, которые удобно показать на примере точения тангенциальными призматическими резцами.

Инструментальная система координат – прямоугольная система координат с началом в вершине лезвия, сориентированная относительно геометрических элементов инструмента, принятых за базу, например задней поверхности (рис.2.4,а). Эта система применяется для изготовления и контроля инструмента.

Статическая система координат – прямоугольная система координат с началом в рассматриваемой точке режущей кромки, сориентированная относительно направления скорости главного дви-жения резания (рис.2.4,б). Эта система используется для приближенного расчета углов инструмента в процессе резания и для учета их изменения после установки инструмента на станке.

Кинематическая система координат – прямоугольная система с началом в рассматриваемой точке лезвия, сориентированная относительно направления скорости результирующего движения резания (рис.2.4,в).

Основная плоскость P_v (см. рис.2.4) – координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания. В инструментальной системе направление скорости главного движения резания для токарных и строгальных резцов принимается перпендикулярно конструкторской установочной базе, у осевых инструментов и фрез – по касательной к траектории вращательного движения инструмента, у долбяков – параллельно оси хвостовика.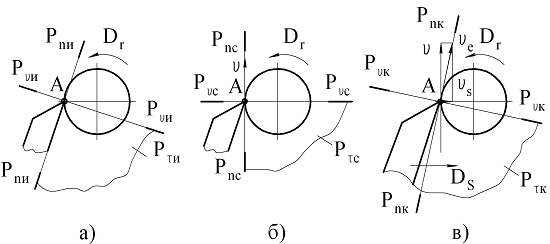

Соответственно системам координат различают инструменталь-ную основную плоскость P_vи (см. рис.2.4,а), статическую основную плоскость P_vc (см. рис.2.4,б) и кинематическую основную плоскость P_vk (см. рис.2.4,в).

Плоскость резания P_n - координатная плоскость, проходящая через главную режущую кромку (или касательно к ней в рассматриваемой точке) и перпендикулярная основной плоскости. В различных системах координат эта плоскость будет соответственно называться инструментальной плоскостью резания P_nи , статической P_nc или кинематической P_nk(см. рис.2.4).

Главная секущая плоскость P_τ - координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания. Соответственно системе координат главная секущая плоскость может быть инструментальной P_τи , статической P_τc и кинематической P_τk (см. рис.2.4).

Координатные плоскости для токарного проходного резца в статической и кинематической системах координат показаны на рис.2.5.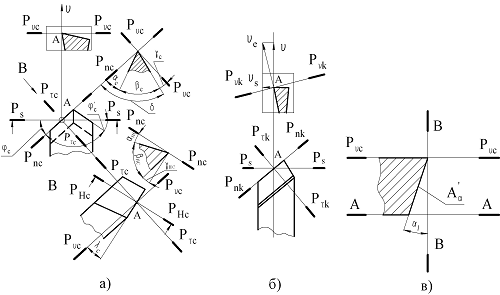

γ- передний угол инструмента - это угол в секущей плоскости между передней поверхностью лезвия и основной плоскостью (см. рис.2.5,а).

γ- главный передний угол - передний угол в главной секущей плоскости; γ_н - нормальный передний угол - это передний угол в нормальной секущей плоскости P_н .

Главные передние углы в зависимости от системы координат могут быть инструментальными γ_н , статическими γ_c и кинематическими γ_k ; эти углы определяются в соответствующей главной секущей плоскости и измеряются между передней поверхностью лезвия и соответствующей основной плоскостью.

γ_p- рабочий кинематический передний угол - угол в секущей плоскости схода стружки между передней поверхностью лезвия и кинематической основной плоскостью.

α- задний угол - угол в секущей плоскости между задней поверхностью лезвия и плоскостью резания; α_н - нормальный задний угол - задний угол в нормальной секущей плоскости ( α_нс на рис.2.5,а).

α- главный задний угол - задний угол в главной секущей плоскости – инструментальный задний угол α_и , статический главный задний угол и кинематический главный задний угол α_k - соответственно в инструментальной, статической и кинематической главной секущей плоскостях.

β- угол заострения - угол в секущей плоскости между передней и задней поверхностями (соответственно главный угол заострения β - в главной секущей плоскости с вариантами – инструментальный главный угол заострения β_и , статический главный угол заострения β_c (см. рис.2.5,а) и кинематический главный угол заострения β_k ); β_н - нормальный угол заострения - угол заострения в нормальной секущей плоскости.

λ- угол наклона кромки - угол в плоскости резания между режущей кромкой и основной плоскостью 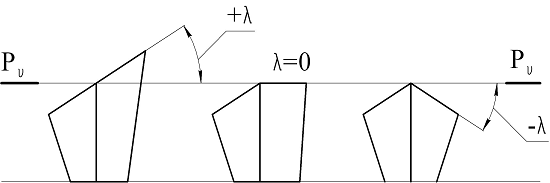(рис.2.6).

Углы λ могут измеряться соответственно в инструментальной, статической и кинематической плоскостях резания и соответствующими основными плоскостями и называются инструментальными λ _и , статическими λ _c или кинематическими λ _k . В зависимости от расположения режущей кромки относительно основной плоскости угол λ может быть (см. рис.2.6) положительным (вершина инструмента является самой низкой точкой лезвия), нулевым (лезвие совпадает с основной плоскостью) и отрицательным (вершина – самая высокая точка).

φ - угол в плане - угол в основной плоскости между плоскостью резания и рабочей плоскостью (см. φ_c на рис.2.5,а).

В зависимости от положения основной плоскости угол в плане будет инструментальным φ_и , статическим φ_c и кинематическим φ_k (см. рис.2.5). Если угол в плане измерять между режущей кромкой и рабочей плоскостью, то получим рабочий кинематический угол в плане φ_p.

Перечисленные выше координатные плоскости и геометрические параметры были даны в соответствии с ГОСТ 25762-83. Этим стандартом не регламентируется вспомогательный угол в плане φ₁ , угол при вершине ε , а также вспомогательный задний угол α₁ и угол резания δ (см. рис.2.5,а), которые влияют на процесс резания.

φ₁ - впомогательный угол в плане - это угол между рабочей плоскостью P_s и проекцией вспомогательной режущей кромки на основную плоскость P_v , угол при вершине резца ε измеряется между проекцией на основную плоскость главного и вспомогательного лезвий инструмента [3].

Угол резания δ измеряется между передней поверхностью и плоскостью резания P_n (см. рис.2.5,а).

Вспомогательный задний угол α₁ лежит в плоскости, нормальной к вспомогательной режущей кромки (на рис.2.5,а сечение не показано), и измеряется между вспомогательной задней поверхностью A'_α и плоскостью BB , перпендикулярной основной плоскости резца AA (см. рис.2.5,в)(AA||P_vP_v) .

Между углами резца в главной секущей плоскости и углами в плане существуют известные соотношения (см. рис.2.5,а):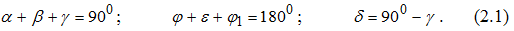

Для отрезных резцов [8] главный угол в плане определяется как угол между плоскостью резания P_n и рабочей плоскость P_s , проведенной через левую вершину резца (точка 1 на рис.2.7). У отрезного резца две вершины (точки 1 и 2), поэтому он имеет два вспомогательных лезвия 1-3 и 2-4 и для каждого из них – углы ε₁ и ε₂ и вспомогательные углы в плане φ'₁ и φ'₂ ; обычно φ'₁ = φ'₂ .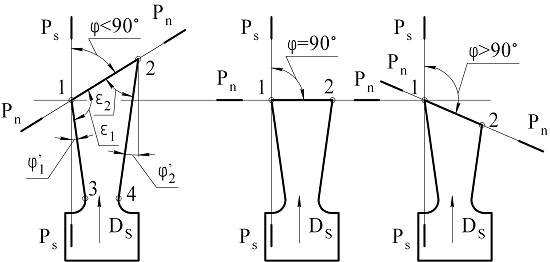

Для других типов режущих инструментов расположение координатных плоскостей имеет некоторую специфику. Например, у спиральных сверл основная плоскость P_v проходит через периферийные точки главных лезвий сверла 1-3 и 2-4 и ось сверла (рис.2.8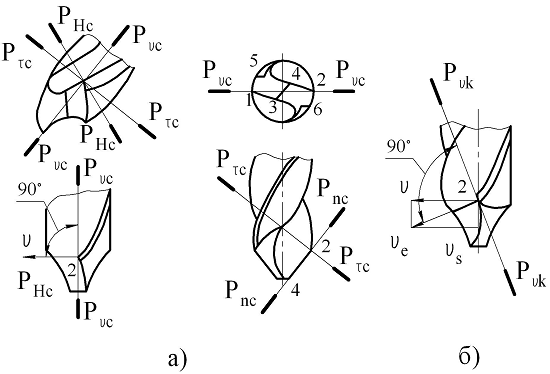,а).

Положения статической и кинематической плоскостей резания показаны соотвественно на рис.2.8,а,б, а углы сверла секущей P_τc и нормальной P_нс плоскостях – на рис.2.9.

Кроме стандартных углов &aplpha; , β ,γ и φ , сверло характеризуется углом при вершине 2φ (двойным углом в плане), углом ψ наклона перемычки (поперечной режущей кромки 3-4 (рис.2.9) и углом ω наклона винтовой стружечной канавки (измеряется между основной плоскостью P_vc и направлением стружечной канавки для периферийной точки 2 главного лезвия сверла 2-4).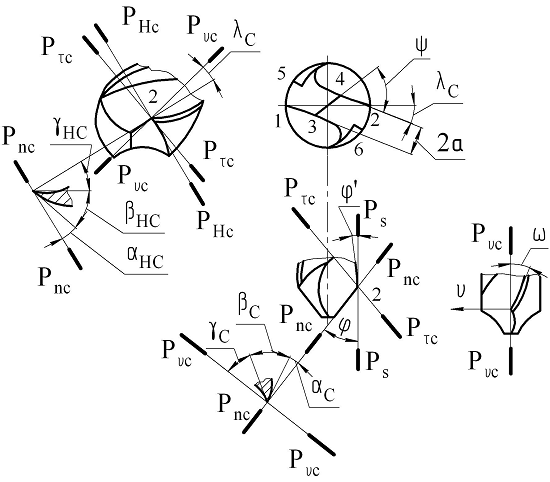

Вспомогательный угол в плане φ₁ на сверлах не регламентируется, а задается величиной обратной конусности. Обычно для сверл ψ=50-55^o , 2φ=90-140^o , ω=0-45^o . Особенностью геометрии спиральных сверл является изменение переднего угла по длине главных режущих кромок 1-3 и 2-4 (см. рис.2.9), причем максимальное значение γ у сверл – на периферии, к центру сверла передние углы уменьшаются и в районе перемычки принимают даже отрицательные значения.