

Размеры срезаемого слоя Точение. В зависимости от формы режущей кромки инструмента, ее расположения относительно образующей обработанной детали, определяемого углом ψ сечение срезаемого слоя (сечение среза) может иметь различную форму [1, 3]. Сечением срезаемого слоя (сечением среза) называется фигура, образованная при рассечении основной плоскостью слоя материала заготовки, отделяемого лезвием за один цикл главного движения резания. При уменьшении угла ψ площадь срезаемого слоя ƒ = t*S0(номинальная площадь) не изменяется: ƒ1=ƒ2=ƒ3 = t*S0 (рис.3.4). Однако срезаемый слой при этом становится более широким, но более тонким. Поэтому глубина резания и подача на один оборот S0 не могут характеризовать полностью физику процесса резания, а являются лишь настроечными величинами для станка, т.е. технологическими факторами. Конфигурация срезаемого слоя характеризуется его толщиной и шириной. Толщина срезаемого слоя (толщина среза) a- длина нормали к поверхности резания, проведенной через рассматриваемую точку режущей кромки, ограниченная сечением срезаемого слоя, т.е. расстояние по нормали между положениями поверхности резания, соответствующими подаче на оборот. Ширина срезаемого слоя (ширина среза) b - длина стороны сечения срезаемого слоя, образованной поверхностью резания, т.е. расстояние по поверхности резания (по лезвию инструмента) между обработанной и обрабатываемой поверхностями детали. Из треугольников cde и mnc (см. рис.3.4) вытекает 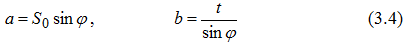 при условии, что λ= 00 , если λ≠0 , то  Номинальная площадь среза  действительная площадь среза будет меньше номинальной (за вычетом площади остаточного гребешка). В зависимости от соотношения между и при продольном точении (рис.3.5) возможны три формы среза: прямой, равнобокий (ромбический) и обратный. 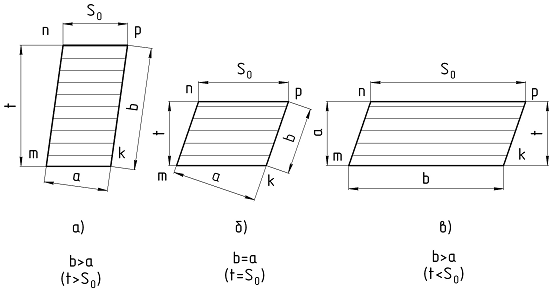 Рис.3.5. Виды срезов при точении: а- прямой; б – равнобокий; в - обратный Для равнобоких срезов b=a , S0sinφ=t/sinφ или . В общем случае, если t/S0>sin2φ - срез прямой, t/S0=sin2φ - срез равнобокий, t/S0 Резание с равнобокими и обратными срезами соответствует чистовому точению (фрезерованию) широкими резцами с большими подачами, а также лезвиями с поперечными режущими кромками. Для протягивания движение подачи отсутствует, а толщина среза a определяется разностью высот (диаметров) соседних зубьев (см. рис.2.12,а); главное движение резания Dr есть поступательное перемещение протяжки. При нарезании внутренних резьб метчиками, имеющими несколько перьев и зубьев на режущей части каждого пера, элементарная толщина среза az , снимаемая одной режущей кромкой, равна (см. рис.2.12,б): 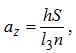 где h - высота зуба; l3 - длина заборного конуса; n - число перьев; S - ход резьбы. Фрезерование. Толщина срезаемого слоя a(рис.3.6) при фрезеровании – величина переменная в пределах угла контакта, которая определяется как расстояние по нормали между последовательными положениями поверхности резания, соответ-ствующими подаче на один зуб [1, 3]. На рис.3.6 размер aψx есть текущее значение толщины среза, соответствующее углу контакта ψx . Для цилиндрических, дисковых и фасонных фрез aψ=amax=ВД . Так как ΔВСД∼ΔОВЕ , то ∠ВСД = ψ и ВД=Szsinψ. Аналогично aψx=Szsinψx . Средняя толщина среза при фрезеровании соответствует половине угла контакта ψ и равна: 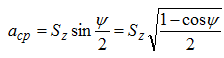 или с учетом (3.3)
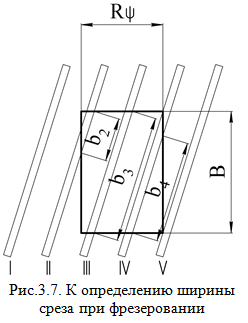
Ширина срезаемого слоя b - длина соприкосновения зуба фрезы с обрабатываемой деталью. Для прямозубой цилиндрической фрезы ширина среза равна ширине фрезерования B (см. рис.3.8), а у фрез с винтовых зубом ширина среза есть величина переменная. Развернув на плоскость дугу врезания AB (см. рис.3.6), получим площадку врезания с размерами Bχ Rψ (рис.3.7), на которой зубья фрезы «отпечатываются» в виде прямых линий. Размеры b2,b3 и b4 - мгновенные значения ширины среза, которая, как видно из рис.3.7, плавно возрастает от нуля до максимального значения и затем уменьшается до нуля. Площадь срезаемого слоя при фрезеровании в любой момент времени есть величина переменная, так как толщина меняется в пределах угла контакта. У прямозубой фрезы текущее значение площади среза для одного зуба: 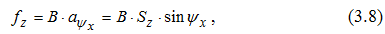 а максимальное 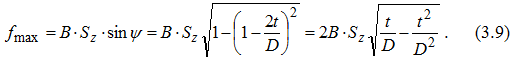 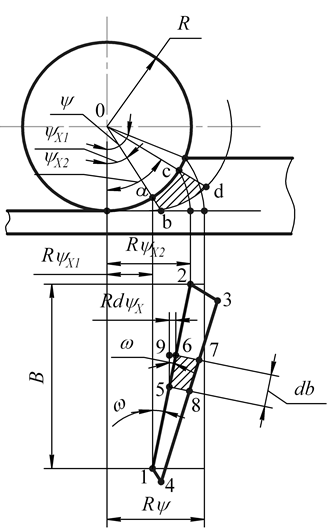 Рис.3.8. К определению площади среза для фрез с винтовым зубом Просмотр рисунка Так как при фрезеровании в пределах угла контакта ψ работает несколько зубьев K (K = ψ/ε ;ε=360o/z , где ε - угловой шаг зубьев), то суммарную площадь среза найдем из (3.8):  При работе цилиндрической прямозубой фрезой каждый зуб по всей длине мгновенно входит в контакт с деталью и мгновенно выходит из соприкосновения с ней. Это приводит к появлению вибраций, снижению качества поверхности и интенсивному износу фрез. Винтовые фрезы работают более спокойно, так как в отличие от прямозубых ширина среза у них плавно возрастает от нуля до максимума и вновь падает до нуля. Найдем площадь срезаемого слоя для этого случая. Развернем на плоскость площадку врезания и отметим на ней мгновенное положение зуба 1-2 и соответствующие толщины среза (рис.3.8): 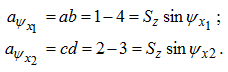 F1-2-3-4 - площадь, срезанная одним зубом. Выделим на этой площади элементарную площадку dFz=F5-6-7-8 ; ее положение определяется промежуточным углом ψx , а ее размеры равны dFz =(5-8)*db=aψx*db=Szdb*sinψx (3.11) Элементарную ширину среза db найдем из треугольника 5-6-9:  где ω - угол наклона зуба фрезы. Из (3.11) и (3.12) имеем:  Интегрируя (3.13) по ψx , получаем: 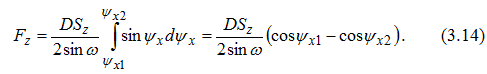 Формула (3.14) получена А.М.Розенбергом [5] для мгновенной площади срезаемого слоя одним зубом. Если в пределах угла контакта одновременно работают k зубьев, то суммарная площадь среза равна: 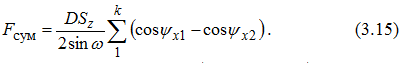 Определение числа одновременно работающих зубьев для фрез с винтовым зубом Фрезы с винтовым зубом работают в более благоприятных условиях, так как в пределах угла контакта их располагается больше, чем у фрез прямозубых. 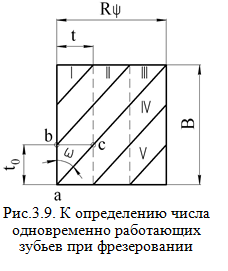
Возьмем площадку врезания и отметим на ней следы зубьев фрезы (рис.3.9). Из схемы видно, что если бы фреза была прямозубой, то в работе одновременно участвовало бы kq=ψo/ε=ψo/360o зубьев, в данном случае два - IV и V. У фрезы с винтовым зубом добавляется еще некоторое количество работающих зубьев, зависящих от B и t0 , т.е. k2=B/t0 , в данном случае еще три - I, II, III. В итоге имеем: 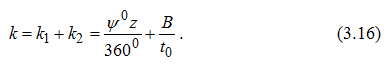 Определим осевой шаг t0 , выразив его через торцевой t: t0=t/tgω(Δabc , рис.3.9). В свою очередь t=πD/z , тогда t=πD/(z*tgω) (3.17) Из (3.16) и (3.17) имеем: k=ψoz/360o+B*ztgω/(πD) (3.18) Равномерное фрезерование. Как видно из формулы (3.15) суммарной площади среза при работе фрезой с винтовым зубом, является величиной переменной, так как изменяются и толщина, и ширина среза. При определенных сочетаниях параметров фрезерования можно получить постоянную площадь срезаемого слоя. Такой вид фрезерования, когда Fсум=const , называется равномерным. Очевидно,Fсум=const , когда Ε(cosψx1-cosψx2)= const (3.19) Равномерное фрезерование осуществимо только при работе фрезы винтовым зубом ( ω≠0) и при условии, что осевой шаг укладывается в ширине фрезерования целое число раз C=B/t0 (3.20) Обычно C выбирается равным 2 или 3. Для примера, на рис.3.9 C=B/t0=3 , а k=5 . Для каждого из пяти одновременно работающих зубьев найдем величину (cosψx1-cosψx2) , определив предварительно углы ψx1 и ψx2 для каждого из k зубьев. Из рис.3.9 следует: 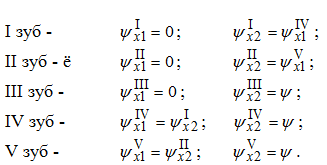 Подставляя в (3.15) значения cosψx1 и cosψx2 для каждого зуба, получаем: 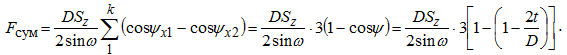 Тогда  Для обеспечения равномерности фрезерования представим (3.20) в виде:  При выбранной ширине фрезерования (ширина фрезеруемой поверхности из детали, задаваемая чертежом) необходимо принять значение , равное 2 или 3, выбрать стандартные значения параметров фрезы, например, диаметр D и число зубьев z и затем по (3.22) рассчитать угол ω у фрезы. Фрезерование против подачи и по подаче. При работе цилиндрическими, концевыми и фасонными фрезами различают следующие схемы резания: - фрезерование против подачи (встречное), когда направление вращения главного движения резания Dr и движения подачи Ds не совпадают (рис.3.10,а); - фрезерование по подаче (попутное), когда направление главного движения резания Dr и движения подачи Ds совпадают (рис.3.10,б). 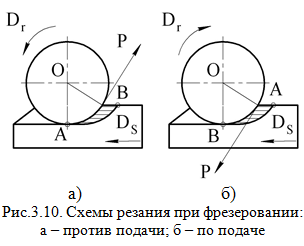
При встречном фрезеровании зуб фрезы начинает работать с минимальной толщиной среза a (в точке A толщина среза a равна нулю), а на выходе толщина среза максимальна. Если фрезерование осуществляется по корке, то зуб фрезы работает из-под корки, «выламывая» ее снизу. Это обстоятельство снижает износ зубьев фрезы при работе по корке. Недостатком фрезерования против подачи является то, что из-за наличия радиуса округления зуба и нулевой толщины среза в момент врезания зуб фрезы проскальзывает и работает по упрочненному слою, образовавшемуся в результате работы впереди идущего зуба. По этой причине наблюдается интенсивный износ задних поверхностей зубьев фрезы. Кроме этого окружная сила стремится оторвать деталь от станка, в результате чего резание сопровождается повышенными вибрациями. При работе по этой схеме возможно и забрасывание стружки зубьями фрезы на обработанную поверхность и ее повреждение. Фрезерование против подачи жаропрочных и нержавеющих материалов вследствие снятия в начальный момент малых толщин среза и интенсивного наклепа, а также пониженной виброустойчивости дает отрицательные результаты [4]. При попутном фрезеровании (рис.3.10,б) в начальный момент зуб фрезы сразу подвергается максимальной нагрузке, так как работает с максимальной толщиной среза, и при наличии корки на заготовке в этом случае стойкость фрезы снижается. Но при обработке без корки сталей средней твердости, жаропрочных и нержавеющих материалов эта схема повышает точность, стойкость фрез, уменьшает шероховатость поверхности на 1-2 класса, так как устраняются недостатки встречного фрезерования – скольжения зуба без резания на некотором участке дуги врезания и низкая виброустойчивость (при попутном фрезеровании заготовка прижимается к станку, стол – к направляющим, поэтому виброустойчивость выше). Данная схема по сравнению с встречным фрезерованием позволяет повысить стойкость цилиндрических фрез при обработке стали 12Х18Н9Т в 2,5-3 раза, а для сплава ЭИ437Б является единственно возможной схемой обработки. Однако при попутном фрезеровании в момент встречи зуба с заготовкой удар максимален, поэтому жесткость станка должна быть высокой, особенно в направлении подачи. Осевой зазор между винтом и гайкой в приводе подачи станка необходимо сводить до минимума (не более 0,1-0,15 мм), применять гидравлический привод подачи или специальные конструкции маточных гаек в механизме подачи станка. |

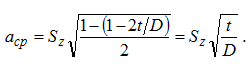 (3.7)
(3.7)