2.1. Определение и исключение систематических погрешностей из результатов наблюдений.

Первичная обработка последовательности результатов измерений одной и той же величины заключается в исключении переменной систематической погрешности с целью исправления результатов измерений и их группирования для получения вариационного ряда.

Для решения инженерных задач вполне достаточно применить графический метод.

Для этого на график по оси ординат наносятся точки с координатами, выражающими значение (результат измерения), а по оси абсцисс – момент времени его получения (или порядковый номер результата). Соединяют точки прямыми линиями и определяют тенденцию изменения результатов измерений. Если тенденция не наблюдается, то считают, что переменная систематическая погрешность несущественна.

Пример решения задачи.

Результаты измерений (в мм) линейного размера изделия, выписанные в том порядке, в каком они были получены, образовали следующий ряд в 30 значений: 40,15; 40,15; 40,15; 40,17; 40,16; 40,16; 40,15; 40,16; 40,16; 40,17; 40,17; 40,17; 40,17; 40,15; 40,18; 40,19; 40,18; 40,18; 40,18; 40,19; 40,19; 40,19; 40,18; 40,21; 40,19; 40,18; 40,19; 40,19; 40,19.

Выполнить обработку ряда измерений, подготовить его для нахождения показателей, характеризующих случайную погрешность измерений, и определить переменную систематическую погрешность выполняемых измерений.

Для рассматриваемой задачи построить график.

В рассматриваемой задаче явно выражена прогрессирующая линейно возрастающая по модулю погрешность. При построении графика на миллиметровой бумаге и исключении систематической погрешности графическим методом, мы получим следующее, а именно: 40,15; 40,15; 40,15; 40,16; 40,15; 40,15; 40,15; 40,14; 40,15; 40,14; 40,15; 40,15; 40,15; 40,15; 40,15; 40,13; 40,15; 40,16; 40,15; 40,15; 40,15; 40,16; 40,15; 40,15; 40,14; 40,17; 40,15; 40,14; 40,14; 40,14; 40,14.

Сгруппировав исправленные результаты, получаем следующий вариационный ряд:

Результаты измерений, мм … 40,13; 40,14; 40,15; 40,16; 40,17

Число результатов ………….. 1 7 18 3 1

2.2. Вычисление среднего арифметического случайной величины и среднего квадратического отклонения после исключения систематической погрешности.

2.2.1. Среднее арифметическое значение определяется:

; ; ,

Где: - значение i-го результата измерения; - вероятность i-го результата измерения;

- число i-х результатов и общее число результатов измерений, соответственно.

2.2.2. Среднее квадратическое отклонение σ результатов определяется:

2.3. Исключение из ряда наблюдений грубых погрешностей (промахов).

Грубая погрешность (промах) – это погрешность результата отдельного измерения, которая для данных условий резко отмечается от остальных результатов.

При однократных измерениях обнаружить грубую погрешность (промах) невозможно.

При многократных измерениях для обнаружения промахов используют статистические критерии.

2.3.1. Критерий «трёх сигм» применяется для результатов измерений, распределённых по нормальному закону. Это простой, но грубый приём. Этим критерием можно пользоваться при числе наблюдений и более.

По этому критерию считается, что результат, возникающий с вероятностью , маловероятен и его можно считать промахом, если .

2.3.2. Критерий Романовского применяется, если число измерений . При этом вычисляется отношение и сравнивается с критерием , выбранным по табл. 1.

Таблица 1

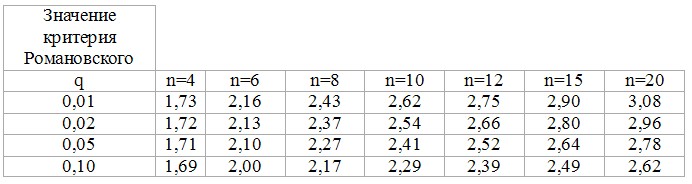Если , то результат считается промахом и отбрасывается.s

Пример. В топливной системе автомобиля результаты пяти измерений расхода топлива составили: 22; 24; 26; 28; 33л на 100км.

Последний результат вызывает сомнение. Проверить не является ли он промахом.

Найдём и σ без учёта последнего результата, т. е. Для четырёх измерений.

Поскольку , то по критерию Романовского при уровне значимости 0,01 и табличный коэффициент . Вычисленное для последнего, пятого измерения

2.3.3. Критерий на основе функции Лапласа применяется, если число измерений .

Проверяемое значение является промахом, если выполняется неравенство .

Предельно допустимое значение определяется по формуле

где - квантиль нормальной функции Лапласа для доверительной вероятности Р. Значения приведены в табл. 2.

2.4. Определение доверительного интервала для среднего значения результатов измерений с заданной доверительной вероятностью.

При прямых многократных измерениях окончательный результат измерений должен быть представлен в форме доверительного интервала:

где - квантиль нормальной функции Лапласа (при ) и коэффициент Стьюдента (при ) для доверительной вероятности Р.

Значения представлены в табл. 2 и табл. 3.

а) При

Таблица 2

б) При

Таблица 3

Пример. Проведено 50 измерений линейного параметра детали. Определить доверительный интервал для среднего значения параметра мм и среднего квадратического отклонения мм при доверительной вероятности Р=0,9. Распределение значений измеренного параметра подчинено нормальному закону.

Решение.

Значение коэффициента выбираем по табл. 2. При Р=0,9 значение .

Определяем доверительный интервал по формуле

Ответ:

2.5. Определение вероятности попадания случайной величины в заданный интервал (границы интервала заданы в табл. 6).

где ; ;
- функция (интеграл) Лапласа, для которой составлены таблицы. Таблица представлена в Приложении А.
Пример. Воспользуемся условием предыдущего примера. Определить вероятность попадания значения параметра в интервал значений 620мм и 750мм.

По условию     =590 (мм); σ=90 (мм);   =620 (мм); =750 (мм)

Определить вероятность Р(620 < x < 750):

Решение

По таблице Приложения А определяем:

P(620 < x < 750)=0,4625-0,1293
Ответ. P(620 < x < 750)=0,3332

2.6. Определение необходимого числа измерений конкретного параметра при заданных значениях погрешности, доверительной вероятности и среднем квадратичном отклонении.

Необходимое число измерений определяется по формуле:

где - значение погрешности при доверительной вероятности .

Значения погрешностей приведены в табл. 7.