Точечные оценки законов распределения результатов наблюдений.

Функции распределения плотности вероятности p(x) описывают поведение непрерывных случайных величин х, значения которых неотделимы друг от друга в некотором конечном или бесконечном интервале. Однако реальное число наблюдений величины х всегда ограничено, и поэтому как результаты наблюдений, так и их случайные погрешности величины дискретные, значения которых поддаются счету. При анализе же дискретных случайных величин возникает задача нахождения точечных оценок параметров их функции распределения на основании выборок — ряда значений х_b, принимаемых случайной величиной х в n независимых опытах.

Оценку параметра называют точечной, если она выражается одним числом. К точечным характеристикам погрешности относятся СКО случайной погрешности и среднее арифметическое значение измеряемой величины.

Задача нахождения точечных оценок — частный случай статистической задачи определения оценок параметров функции распределения случайной величины на основании выборки. В отличие от самих параметров их точечные оценки являются случайными величинами, значения которых зависят от объема экспериментальных данных, а закон распределения — от законов распределения самих случайных величин.

К точечным оценкам предъявляются требования состоятельности, несмещенности и эффективности.

Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики.

Hесмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике. Требование несмещенности на практике не всегда целесообразно, так как оценка с небольшим смещением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не всегда удается удовлетворить одновременно все три этих требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных точек зрения

Эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Оценим математическое ожидание m и СКО σ для ограниченной группы (выборки) наблюдений, обозначив их через хi Результат измерений при распределении наблюдений по нормальному закону определяют, учитывая известную в теории вероятностей закономерность (закон больших чисел): при достаточно большом числе n независимых наблюдений х_i среднее арифметическое значений случайной величины приближается к ее математическому ожиданию т определяемому подобно оценке по формуле

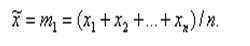(4.4)

Соответственно, при оценке СКО σ используют выражение для СКО σ, справедливое для достаточно больших n:

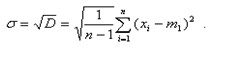(4.5)

Для оценки рассеяния отдельных результатов измерения (х_i) относительно среднего арифметического значения определяют оценку СКО этого среднего арифметического

Применение формулы (4.6) правомерно при условии постоянства измеряемой величины х в процессе измерения. Если при измерении величина х изменяется, как, например, при измерении потенциала проводника через равные отрезки длины, то в формуле (4.6) в качестве т следует брать какую-то постоянную величину, например, начало отсчета. Формулы (4.5) и (4.6) связаны соотношением

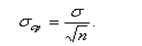(4.7)

Среднее арифметическое значение из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого отдельного измерения. Это и отражает формула (4.7), определяющая фундаментальный закон теории погрешностей, из которого следует, что если требуется повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если необходимо повысить точность в 3 раза, то число измерений увеличивается в 9 раз и т. д. При этом необходимо четко разграничивать применение средних квадратических отклонений σ ср и σ: величину σ ср применяют при оценке погрешностей окончательного результата, σ — при оценке погрешности метода измерения.

Интервальные оценки законов распределения результатов наблюдений.

Достоверность любого измерения зависит от степени доверия к его результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных границах или интервале действительного значения.

К интервальным характеристикам погрешности относятся границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они определяются как доверительные интервалы, а границы (окрестности) — доверительными границами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными (безусловными) интервалами.

Оценку случайных погрешностей с помощью доверительного интервала называют интервальной, а доверительный интервал определяют с использованием квантилъных оценок погрешностей.