Выполнение работы

Задание 1. Определение углового коэффициента упругости пружины

1. Для определения углового коэффициента упругости закрепите стержень на вращающемся валу (рис.1). Кольцо динамо-метра оденьте на стержень на расстоянии r от оси вращения (это плечо силы). Линейкой измерьте плечо силы. Под действием момента силы М = Fr поверните стержень на угол j. При измерении силы динамометр должен находиться под прямым углом к плечу рычага.
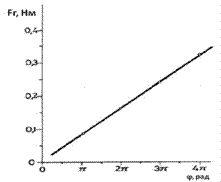
Рис.22. Измерьте силу при помощи динамометра для углов поворота стержня p, 2p, 3p, 4p. Исходя из требований к безопасности и устойчивости, не рекомендуется перегибать пружину на ± 720º. 3. Построить график зависимости момента силы спиральной пружины от угла ее закручивания. Из графика (рис.2) находим тангенс угла наклона, численное значение которого равно угловому коэффициенту упругости пружины.

Задание 2. Определение момента инерции твердого тела
1. Закрепите однородный цилиндр на вращающемся валу (рис.1).
2. Для измерения периода колебаний на диск прикрепите листок бумаги (ширина ≤ 3 мм). Разместите тело так, чтобы листок находился точно под световым барьером. Для светового барьера выберите режим . Отклоните тело на угол j » 90º. Нажатием кнопки в верхнем левом углу включите световой барьер и освободите диск. Несколько раз (3-5) измерьте период колебаний диска.
3. По среднему значению периода определите момент инерции однородного цилиндра I по формуле (9).
4. С помощью рычажных весов измерьте массу цилиндра, а рулеткой - радиус цилиндра.
5. Найдите теоретическое значение момента инерции цилиндра Iтеор.
6. Результаты измерений и вычислений занесите в таблицу 1.

Таблица 1

Ц И Л И н Д Р	№ п/п	Т	I	m	R	Iтеор	DI	e
	№ п/п	с	кгм2	кг	м	кгм2	кгм2	%
	1 2 3 : 5
	Ср.

7. Сравните результаты эксперимента с теоретическим значением момента инерции цилиндра, оцените погрешность по формуле: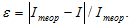
Примечание. Алгоритм обработки прямых и косвенных измерений приведен в приложении.

Задание 3. Установление зависимости момента инерции двух грузиков от их расстояния до оси вращения

1. Закрепите стержень на вращающемся валу (рис.1).
2. Счетчик расположить так, чтобы при колебаниях стержня его конец пересекал световой барьер.
3. Несколько раз (3-5) измерьте период колебаний Т стержня.
4. По среднему значению периода по формуле (9) определите момент инерции однородного стержня I.
5. Закрепите на стержне два груза на одинаковом и минимальном расстоянии от оси вращения. Повторите пункты 3-4 для нагруженного стержня и определите момент инерции нагруженного стержня I0.
6. Вычислите момент инерции двух грузов относительно оси вращения: Iгр = I0 – I.
7. Повторите пункты 5, 6 для 5 – 7 различных расстояний грузов до оси вращения.
8. Принимая грузы за материальные точки, по известной их массе рассчитать для каждого расстояния теоретическое значение момента инерции по формуле: Iгр теор = 2mr2.
9. Результаты измерений и вычислений занесите в таблицу 2.

Таблица 2

№ п/п	Т	I	r	Т0	I0	IГР	Iгр Теор
№ п/п	с	кг м2	м	с	кг м2	кг м2	кг м2
1 2 3 4 5 . . 7
Ср.

10. В одних координатных осях постройте графики зависимостей: IГР (r), Iгр теор (r).
11. Сравните результаты эксперимента с теоретическим значением момента инерции грузов, сделайте вывод.

Главная страница	Содержание	Скачать архив