Краткая теория
Закрепим твердое тело (шар или диск, или цилиндр и т.д.) на вращающийся вал и повернем его на угол j » 30°. Если систему предоставить самой себе, то возникнут свободные крутильные колебания под действием момента силы упругости спиральной пружины:
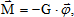 (1)
(1)
где G - угловой коэффициент упругости спиральной пружины.
В реальных условиях маятник под действием моментов сил трения в подшипниках и сопротивления воздуха совершает затухающие колебания. Суммарный момент сил трения зависит от угловой скорости
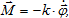 (2) (2)
где k- коэффициент пропорциональности, зависящий от формы и размеров маятника и вязкости среды.
Основное уравнение динамики вращательного движения с учетом уравнений (1) и (2) имеет вид
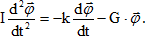 . (3) . (3)
Разделив (3) на момент инерции и вводя коэффициент затухания 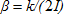 и собственную частоту свободных колебаний и собственную частоту свободных колебаний
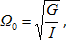 , (4) , (4)
запишем дифференциальное уравнение свободных колебаний в виде:
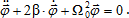 . (5) . (5)
Решением дифференциального уравнения (5) является зависимость модуля углового перемещения от времени
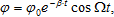 (6) (6)
где циклическая частота свободных колебаний равна
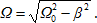 (7) (7)
При слабом затухании 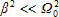 , а уравнения (6) и (7) примут вид: , а уравнения (6) и (7) примут вид:
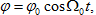 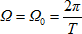 (8) (8)
где Т - период свободных колебаний.
Совместное решение уравнений (4) и (8) позволяет определить момент инерции твердого тела по его периоду крутильных колебаний:
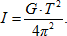 (9) (9)
|
