6. ПОСТОЯННЫЙ ТОК
6.1. Сила тока, плотность тока
Под электрическим током понимают упорядоченное движение заряженных частиц, причем за направление тока принимают направление движения положительных зарядов.
Электрический ток существует при наличии свободных зарядов и электрического поля. Такие условия для движения зарядов можно создать в вакууме (термоэлектронная эмиссия) и в различных средах, таких как твердые тела (металлы, полупроводники), жидкости (жидкие металлы, электролиты) и в газах. Носителями тока могут быть различные частицы, так в металлах – свободные электроны, в газах – электроны и ионы и т.д.
Протекание тока по проводнику характеризует сила тока I, определяемая по формуле:
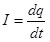 , (6.1) , (6.1)
где dq – заряд, проходящий через поперечное сечение проводника за время dt.
Для постоянного тока величина I остается одинаковой и по модулю, и по направлению, что позволяет в формуле (6.1) выбирать конечные значения заряда и времени:
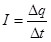 или или 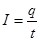 . .
Распределение тока по сечению проводника характеризует вектор плотности 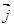 , направление которого в каждой точке проводника совпадает с направлением тока, т.е. с направлением скорости , направление которого в каждой точке проводника совпадает с направлением тока, т.е. с направлением скорости 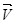 упорядоченных положительных зарядов упорядоченных положительных зарядов 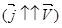 . Модуль вектора . Модуль вектора 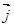 равен: равен:
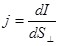 , ,
где dl- сила тока, протекающего в данной точке внутри проводника через элементарную площадку 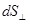 , расположенную перпендикулярно к направлению тока (рис.6.1,а). , расположенную перпендикулярно к направлению тока (рис.6.1,а).
В этой формуле угол 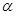 – это угол между вектором – это угол между вектором 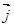 и нормалью и нормалью 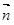 к элементарной площадке площадью к элементарной площадке площадью 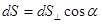 (см.рис.6.1,а). (см.рис.6.1,а).
Представляет интерес выразить вектор плотности тока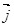 через характеристики, описывающие движение свободных зарядов в проводнике. В качестве примера рассмотрим электрический ток в металле, где валентные электроны образуют газ свободных частиц, заполняющих кристаллическую решетку положительно заряженных ионов. через характеристики, описывающие движение свободных зарядов в проводнике. В качестве примера рассмотрим электрический ток в металле, где валентные электроны образуют газ свободных частиц, заполняющих кристаллическую решетку положительно заряженных ионов.
При отсутствии электрического поля в проводнике свободные электроны участвуют только в тепловом движении со средней арифметической скоростью 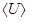 , определяемой по формуле , определяемой по формуле
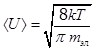 , ,
где k - постоянная Больцмана, 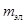 - масса электрона, T - температура. При комнатной температуре - масса электрона, T - температура. При комнатной температуре 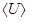 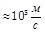 . .
Из-за хаотичности теплового движения электронов электрического тока не возникает (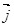 =0), так как через поперечное сечение проводника в обе стороны проходит одинаковое число электронов, и поэтому суммарный перенос заряда равен нулю. =0), так как через поперечное сечение проводника в обе стороны проходит одинаковое число электронов, и поэтому суммарный перенос заряда равен нулю.
При включении электрического поля у электронов появляется добавочная скорость 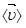 - средняя скорость направленного движения под действием сил электрического поля. Именно - средняя скорость направленного движения под действием сил электрического поля. Именно 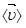 обеспечивает наличие тока в проводнике. обеспечивает наличие тока в проводнике.
Через поперечное сечение проводника площадью S за время t пройдут все электроны, находящиеся в цилиндре высотой (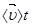 ) (см.рис.6.1,б). Если ввести такую характеристику металла, как концентрацию свободных электронов, то тогда можно получить: ) (см.рис.6.1,б). Если ввести такую характеристику металла, как концентрацию свободных электронов, то тогда можно получить:
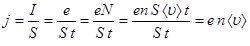 , (6.3) , (6.3)
где e – заряд электрона или, в общем случае, свободной заряженной частицы, участвующей в создании электрического тока; N – число заряженных частиц в объеме V.
Приведем оценку модуля средней скорости направленного движения свободных электронов в металле 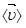 . Учитывая числовые значения концентрации свободных электронов в металле n ~ 1029 м-3 и предельно допустимую плотность тока, например, в медном проводнике jпред ~ 107 А/м2, из формулы (6.3) получим: . Учитывая числовые значения концентрации свободных электронов в металле n ~ 1029 м-3 и предельно допустимую плотность тока, например, в медном проводнике jпред ~ 107 А/м2, из формулы (6.3) получим:
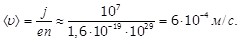
Из последнего выражения следует, что скорость <v> упорядоченного движения значительно меньше скорости теплового движения.
6.2. Закон Ома для однородного участка цепи.
Сопротивление проводников.
Понятие о сверхпроводимости
Однородным участком электрической цепи называют участок, на котором направленное движение зарядов происходит под действием только кулоновских сил. Для него Г. Ом в 1826 году экспериментально установил следующий закон: сила тока I, текущего по однородному участку цепи, прямо пропорциональна разности потенциалов (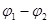 ) и обратно пропорциональна сопротивлению R этого участка цепи: ) и обратно пропорциональна сопротивлению R этого участка цепи:
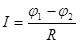 , (6.4) , (6.4)
где разность потенциалов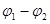 между начальной и конечной точками участка. между начальной и конечной точками участка.
Формула (6.4) позволяет установить единицу сопротивления – ом (Ом): 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.
Сопротивление однородного участка цепи R характеризует свойство проводника препятствовать протеканию по нему электрического тока:
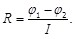
Cопротивление не зависит ни от 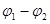 , ни от I и связано с геометрическими размерами, формой проводника, материалом, из которого проводник изготовлен, и температурой. , ни от I и связано с геометрическими размерами, формой проводника, материалом, из которого проводник изготовлен, и температурой.
На практике обычно используют проводники цилиндрического вида длиной 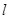 и площадью поперечного сечения S. Для однородного линейного проводника R определяется: и площадью поперечного сечения S. Для однородного линейного проводника R определяется:
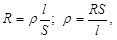 (6.5) (6.5)
где 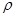 - характеризует материал проводника и называется удельным электрическим сопротивлением. Единица удельного электрического сопротивления – ом-метр (Ом?м). Численно - характеризует материал проводника и называется удельным электрическим сопротивлением. Единица удельного электрического сопротивления – ом-метр (Ом?м). Численно 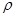 равно сопротивлению R проводника при равно сопротивлению R проводника при 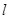 =1 м и S = 1 м2. =1 м и S = 1 м2.
Для чистых металлических проводников при комнатной температуре удельное сопротивление практически линейно возрастает с повышением температуры t, а именно:
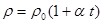 , (6.6) , (6.6)
где 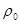 - удельное сопротивление проводника при температуре - удельное сопротивление проводника при температуре 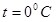 . .
Входящий в формулу (6.6) параметр 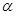 называют температурным коэффициентом сопротивления (ТКС), он численно равен относительному изменению удельного сопротивления проводника называют температурным коэффициентом сопротивления (ТКС), он численно равен относительному изменению удельного сопротивления проводника 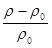 при повышении температуры проводника на 10С: при повышении температуры проводника на 10С:
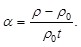
Зависимость R(t) металлического проводника также соответствует формуле (6.6), так как размеры проводника (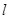 , S) обычно изменяются с температурой значительно слабее, чем удельное сопротивление: , S) обычно изменяются с температурой значительно слабее, чем удельное сопротивление:
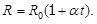
Для чистых металлов ТКС является положительной величиной, примерно равной 1/273 К-1. При низких температурах, когда колебания положительных ионов кристаллической решетки не оказывают существенного влияния на движение свободных электронов, удельное сопротивление 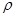 не слишком изменяется с температурой (рис.6.2, кривая 1). не слишком изменяется с температурой (рис.6.2, кривая 1).
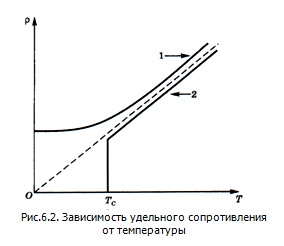
Для многих металлов при определенной температуре Тс (ее называют температурой перехода в сверхпроводящее состояние, Тс ≤ 20 К) сопротивление металла R обращается в ноль (R = 0), металл при Т < Тс будет находиться в сверхпроводящем состоянии (рис.6.2, кривая 2).
Отметим, что ТКС может уменьшаться с повышением температуры, что, например, наблюдается для растворов электролитов и для полупроводников и связано с увеличением в них концентрации свободных носителей заряда при повышении температуры.
Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.
6.3. Источники тока. ЭДС источника тока. Напряжение.
Закон Ома для неоднородного участка цепи
Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (предполагается что они положительные) от точек с бÓльшим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.
Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе – за счет механической энергии вращения ротора генератора и т.п. Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.
Источник тока и потребители тока (сопротивление R) составляют замкнутую цепь (рис.6.3).
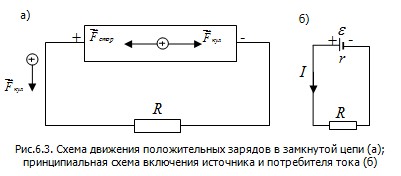
Источник тока можно охарактеризовать сопротивлением r (сопротивление внутренней части цепи) и электродвижущей силой (ЭДС) ε – она определяет работу сторонних сил по перемещению единичного положительного заряда в один кулон от отрицательного полюса к положительному
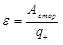 . .
Изображение источника тока на схемах приведено на рис.6.3,б.
Нужно отметить, что выделение в электрической цепи отдельного участка, на котором действуют сторонние силы, не всегда возможно. Сторонние силы могут действовать на всех участках цепи. Например, ЭДС индукции возникает во всех точках проводящего контура, находящегося в переменном во времени магнитном поле.
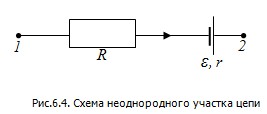
Участок цепи, где одновременно действуют сторонние и кулоновские силы, называют неоднородным участком цепи (рис.6.4). Работу кулоновских сил по перемещению электрического заряда на этом участке характеризует разность потенциалов (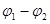 ), а работу сторонних сил – действующая на этом участке цепи ЭДС ε1,2: ), а работу сторонних сил – действующая на этом участке цепи ЭДС ε1,2:
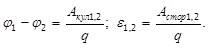 (6.7) (6.7)
Для неоднородного участка цепи вводится новая величина, называемая напряжением U1,2, она характеризует общую работу сторонних и кулоновских сил на неоднородном участке цепи при перемещении единичного положительного заряда:
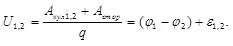 (6.8) (6.8)
На однородном участке цепи (E1,2=0) напряжение равно разности потенциалов:
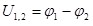
Для описания силового действия на помещенные в поле сторонних сил заряды (по аналогии с электростатическим полем) вводят его силовую характеристику – напряженность поля сторонних сил 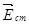 : :
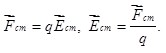
Тогда формулы (6.7) и (6.8) можно представить в виде:
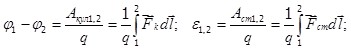
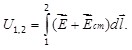 (6.9) (6.9)
Для ЭДС ε, действующей в замкнутой цепи, из выражения (6.9) получим
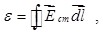
т.е. ЭДС ε равна циркуляции вектора напряженности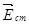 сторонних сил по произвольному замкнутому контуру. Это свидетельствует о том, что поле сторонних сил в отличие от электростатического поля, не является потенциальным. сторонних сил по произвольному замкнутому контуру. Это свидетельствует о том, что поле сторонних сил в отличие от электростатического поля, не является потенциальным.
6.4. Работа, мощность и тепловое действие
постоянного тока
Рассмотрим участок цепи, не содержащий ЭДС (рис. 6.5). На этом участке приложена разность потенциалов, и идет ток I. За некоторый промежуток времени t через участок пройдет заряд q=It. При этом силы электрического поля совершат работу по переносу зарядаq от точки с более высоким к точке с более низким потенциалом:
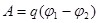 . .
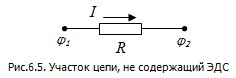
В соответствии с законом Ома (6.4) эту работу можно выразить через сопротивление участка R:
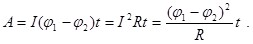
Если на участке цепи находится источник тока (см.рис.6.4), то при переносе заряда q работу совершают как силы электрического поля, так и сторонние силы:
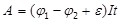 или или 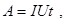
где 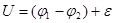 - напряжение на участке цепи, содержащем ЭДС. - напряжение на участке цепи, содержащем ЭДС.
Полная работа электрических сил в замкнутой цепи равна нулю, так как в одной части цепи ток течет по полю, а в другой части – против поля. Внутри источника тока работают сторонние силы; они разделяют заряды, создают электрическое поле и запасают энергию. Эта энергия расходуется во внешней цепи на поддержание в ней электрического тока. Поэтому, в конечном счете, в замкнутой цепи совершает работу только приложенная ЭДС.
Мощность определяется работой, совершенной за единицу времени
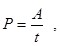
для участка цепи 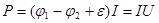 ; ;
для замкнутой цепи 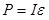
Мощность, выделяемая во внешней цепи,
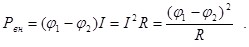
Для поддержания в цепи постоянного тока необходимо совершать работу А; энергия электрического тока в проводнике непрерывно расходуется и переходит в другие формы энергии. Действительно, опыт показывает, что проводник, по которому течет ток, нагревается, и в нем выделяется некоторое количества тепла Q. Если при этом не возникает никаких других форм энергии (например, механической), то по закону сохранения энергии
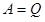 или или 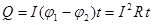 . (6.10) . (6.10)
Выражение (6.10) определяет количество теплоты, выделяемое при прохождении тока в проводнике. Его называют законом Джоуля-Ленца.
6.5. Законы Ома и Джоуля-Ленца
в дифференциальной форме
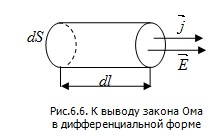 Рассмотрим изотропный однородный проводник, в котором упо-рядоченное движение носителей тока происходит в направлении вектора Рассмотрим изотропный однородный проводник, в котором упо-рядоченное движение носителей тока происходит в направлении вектора 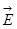 . Тогда направления векторов . Тогда направления векторов 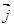 и и 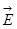 совпадают. Выделим мысленно в окрестности некоторой точки проводника элементарный объем в виде цилиндра с образующими, параллельными векторам совпадают. Выделим мысленно в окрестности некоторой точки проводника элементарный объем в виде цилиндра с образующими, параллельными векторам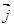 и и 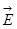 (рис.6.6). Через поперечное сечение цилиндра течет ток силой jdS. Напряжение, приложенное к цилиндру, равно Edl, где (рис.6.6). Через поперечное сечение цилиндра течет ток силой jdS. Напряжение, приложенное к цилиндру, равно Edl, где 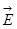 - напряженность поля в данной точке. Сопротивление цилиндра, согласно - напряженность поля в данной точке. Сопротивление цилиндра, согласно
формуле (6.5), равно 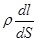 . Подставив эти выражения в формулу (6.4) и учитывая, что для однородного проводника напряжение . Подставив эти выражения в формулу (6.4) и учитывая, что для однородного проводника напряжение 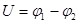 , получим: , получим:
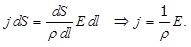
Воспользовавшись тем, что векторы 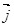 и и 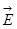 имеют одинаковое направление, можно написать имеют одинаковое направление, можно написать
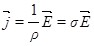 (6.11) (6.11)
Обратная 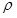 величина величина 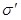 называется удельной электрической проводимостью материала. Единицей называется удельной электрической проводимостью материала. Единицей 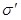 является сименс на метр (См/м). является сименс на метр (См/м).
Введем удельную тепловую мощность W:
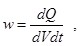
она определяет количество теплоты dQ, выделяемое в элементарном (бесконечно малом) объеме dV, расположенном вблизи точки, взятой внутри проводника, за малое время dt.
Для рассматриваемого здесь вывода вместо элементарных значений dQ, dV, dt можно подставить их конечные значения Q, V, t и, используя закон Джоуля-Ленца (6.10), получим
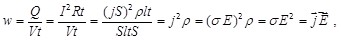
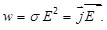 (6.12) (6.12)
Формулы (6.11) и (6.12) представляют собой дифференциальную форму законов Ома и Джоуля-Ленца.
В случае неоднородного участка цепи, когда в проводнике одновременно действуют сторонние и кулоновские силы, формулы (6.11) и (6.12) примут вид:
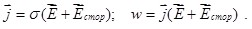
6.6. Правила Кирхгофа
Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. У з л о м называется точка, в которой сходится более чем два проводника (рис. 6.7). Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла – имеющий другой знак (минус или плюс).
Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
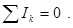 (6.13) (6.13)
Например, для рис. 6.7 первое правило Кирхгофа запишется так:
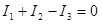 . .
Уравнение (6.13) можно написать для каждого из N узлов цепи. Однако независимыми являются только N-1 уравнений, N-е будет следствием из них.
Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (см., например, контур 1-2-3-4-1 на рис.6.7). Зададимся направлением обхода (например, по часовой стрелке, как указано на рис.6.7) и применим к каждому из неразветвленных участков контура закон Ома:
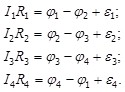
При сложении этих выражений потенциалы сокращаются, и получится уравнение
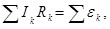 (6.14) (6.14)
которое выражает второе правило Кирхгофа.
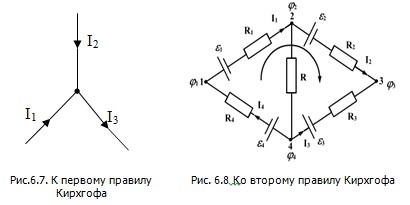
Уравнение (6.14) может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга. Так, например, для цепи, изображенной на рис.6.7, можно составить только три уравнения:
- для контура 1-2-3-4-1;
- для контура 2-3-4-2;
- для контура 1-2-4-1.
При расчете цепей по правилам Кирхгофа необходимо:
1) выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным – его истинное направление противоположно выбранному;
2) выбрать направление обхода контура и строго его придерживаться; произведение IR положительно, если ток на данном участке совпадает с направлением обхода, и наоборот, ЭДС, действующие по выбранному направлению обхода, считаются положительными, против – отрицательными;
3) составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных. |
|
|
