5. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
5.1. Энергия системы зарядов
Получим выражение для потенциальной энергии системы двух точечных зарядов 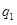 и и 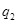 , находящихся на расстоянии r12. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют, и энергия в этом случае равна нулю. При сближении зарядов на расстояние r12 совершается работа против сил электрического поля, которая идет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая qi к , находящихся на расстоянии r12. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют, и энергия в этом случае равна нулю. При сближении зарядов на расстояние r12 совершается работа против сил электрического поля, которая идет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая qi к 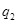 или или 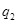 к qi.Работа переноса заряда qi из бесконечности в точку, удаленную от к qi.Работа переноса заряда qi из бесконечности в точку, удаленную от 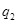 на r12, равна на r12, равна
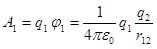 , ,
где 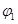 - потенциал, создаваемый зарядом - потенциал, создаваемый зарядом 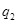 в той точке, в которую перемещается заряд qi. Аналогично работа переноса заряда в той точке, в которую перемещается заряд qi. Аналогично работа переноса заряда 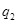 из бесконечности в точку, удаленную от qi на r21, равна из бесконечности в точку, удаленную от qi на r21, равна
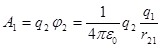 , ,
где 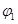 2 - потенциал, создаваемый зарядом qi в той точке, в которую перемещается заряд 2 - потенциал, создаваемый зарядом qi в той точке, в которую перемещается заряд 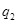 . .
Значение работ в обоих случаях одинаково и каждое из них выражает энергию системы:
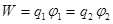 . .
Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:
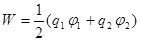 . (5.1) . (5.1)
Формула (5.1) задает энергию системы двух зарядов. Перенесем из бесконечности еще один заряд q3 и поместим его в точку, находящуюся на расстоянии 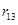 от qi и от qi и 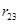 от от 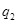 . При этом совершается работа . При этом совершается работа
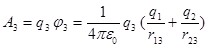 , ,
где ф3 - потенциал, создаваемый зарядами q1 и q2 в той точке, в которую перемещается заряд q3.
В сумме с A1 и A2 работа A3 будет равна энергии трех зарядов:
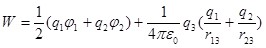 . (5.2) . (5.2)
Выражение (5.2) можно привести к виду:
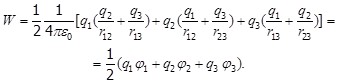
Добавляя к системе зарядов последовательно q4 и qj т.д., можно убедиться в том, что в случае N зарядов потенциальная энергия системы равна:
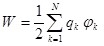 , (5.3) , (5.3)
где 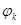 - потенциал, создаваемый в той точке, где находится - потенциал, создаваемый в той точке, где находится 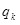 , всеми зарядами, кроме k-го. , всеми зарядами, кроме k-го.
5.2. Энергия заряженного проводника
Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов, а следовательно, энергия заряженного проводника может быть определена по формуле (5.3). Известно, что область, занятая проводником, является эквипотенциальной, поэтому 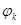 = =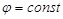 . Вынесем . Вынесем 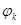 в формуле (5.3) за знак суммы: в формуле (5.3) за знак суммы:
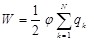
так как 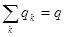 и определяет весь заряд, сосредоточенный на проводнике, выражение для энергии заряженного проводника получим в виде: и определяет весь заряд, сосредоточенный на проводнике, выражение для энергии заряженного проводника получим в виде: 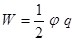 . .
Применяя соотношение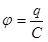 можно получить следующее выражение для потенциальной энергии заряженного проводника: можно получить следующее выражение для потенциальной энергии заряженного проводника:
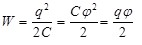 . .
5.3. Энергия заряженного конденсатора
Пусть заряд 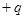 находится на обкладке с потенциалом находится на обкладке с потенциалом 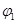 , а заряд , а заряд 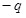 на обкладке с потенциалом на обкладке с потенциалом 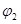 . Согласно формуле (5.3) энергию такой системы можно определить: . Согласно формуле (5.3) энергию такой системы можно определить:
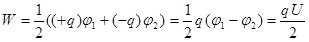 . (5.4) . (5.4)
Воспользовавшись выражением (4.4) для электроемкости конденсатора, (5.4) можно представить в виде:
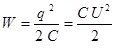 . (5.5) . (5.5)
5.4. Энергия электростатического поля
Энергию заряженного конденсатора можно выразить через величины, характеризующие поле между пластинами. Сделаем это для плоского конденсатора. Учитывая формулу для плоского конденсатора и что 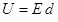 , (5.5) примет вид: , (5.5) примет вид:
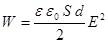 . (5.6) . (5.6)
Так как 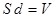 - объем, занимаемый полем, то формулу (5.6) можно записать в виде: - объем, занимаемый полем, то формулу (5.6) можно записать в виде:
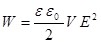 . (5.7) . (5.7)
Формула (5.5) связывает энергию конденсатора с зарядом на его обкладках, а формула (5.7) – с напряженностью поля. В рамках электростатики невозможно ответить на вопрос, что является носителем энергии – заряды или поле? Постоянные поля и создающие их заряды не могут существовать обособленно друг от друга. Законы электродинамики доказывают, что носителем энергии является поле.
Если поле однородно (например, в плоском конденсаторе), энергия в нем распределяется с постоянной плотностью, значение которой можно найти по формуле:
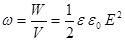 . (5.8) . (5.8)
С учетом взаимосвязи напряженности и индукции поля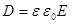 выражения для плотности энергии (5.8) можно записать следующим образом: выражения для плотности энергии (5.8) можно записать следующим образом:
.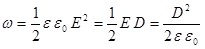
Принимая во внимание (3.7), получим:
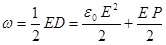 . (5.9) . (5.9)
Первое слагаемое в (5.9) определяет плотность энергии в вакууме, а второе – плотность энергии, затрачиваемую на поляризацию диэлектрика. |
|
|
