4. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
4.1. Распределение избыточного заряда на проводниках
в состоянии равновесия
Проводники – это вещества, в которых есть свободные носители зарядов, способные перемещаться под действием внешнего электрического поля. В случае металлических проводников свободными носителями заряда являются валентные электроны, которые образуют газ, заполняющий кристаллическую решётку положительно заряженных ионов.
Если проводящему телу сообщить некоторый заряд q, то он распределится так, чтобы соблюдались условия равновесия. В условиях равновесия избыточного заряда справедливы следующие утверждения:
- Электрическое поле внутри проводника
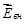 отсутствует, а объём проводника и его поверхность являются эквипотенциальными: отсутствует, а объём проводника и его поверхность являются эквипотенциальными:
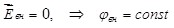 . (4.1) . (4.1)
Действительно, если равенства (4.1) не выполняются, то тогда свободные заряды в проводнике будут перемещаться, так как работа сил электрического поля не будет равна нулю (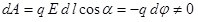 ). Это противоречит условию равновесия избыточного заряда: в условиях равновесия они должны быть неподвижными. ). Это противоречит условию равновесия избыточного заряда: в условиях равновесия они должны быть неподвижными.
- Из-за кулоновского отталкивания одноимённых зарядов избыточные заряды стремятся разойтись на максимально большое расстояние между собой. Кроме того, согласно (4.1) и теореме Гаусса (1.21) сумма зарядов внутри проводника будет равна нулю. Следовательно, при равновесии ни в каком месте внутри проводника не может быть избыточных зарядов – все они распределятся по поверхности проводника.
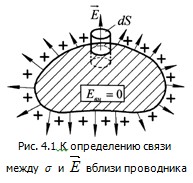
- Распределение избыточных зарядов на внешней поверхности проводника является неравномерным. Установим связь между поверхностной плотностью заряда σ и напряжённостью поля
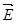 вблизи поверхности заряженного проводника. Для этого построим цилиндрическую поверхность площадью основания dS таким образом, что образующая цилиндра перпендикулярна поверхности проводника, а основания – одно вне, а другое внутри проводника (рис. 4.1). вблизи поверхности заряженного проводника. Для этого построим цилиндрическую поверхность площадью основания dS таким образом, что образующая цилиндра перпендикулярна поверхности проводника, а основания – одно вне, а другое внутри проводника (рис. 4.1).
Поток вектора 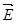 пронизывает только верхнее основание поверхности, так как поля внутри проводника нет пронизывает только верхнее основание поверхности, так как поля внутри проводника нет
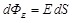 . .
Заряд внутри поверхности 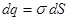 по теореме Гаусса (1.21): по теореме Гаусса (1.21):
 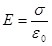 . (4.2) . (4.2)
Из формулы (4.2) следует, что в точках, где больше 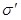 , там больше и напряжённость поля. , там больше и напряжённость поля.
Из-за взаимного отталкивания избыточные заряды стремятся расположиться как можно дальше друг от друга, поэтому на выступах (остриях) проводника поверхностная плотность заряда проводника больше, чем в других местах. Следовательно, вблизи таких частей заряженного проводника напряжённость поля больше, а эквипотенциальные поверхности проходят гуще (рис.4.2).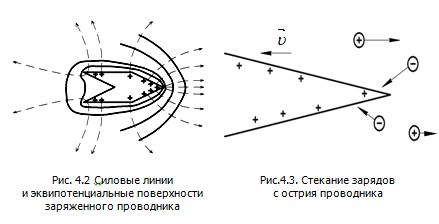
Вблизи поверхности острия (рис.4.3) модуль вектора 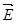 может превысить значение, соответствующее ионизации воздуха (при нормальном атмосферном давлении Е’≈3*106 В/м), что приводит к возникновению стекания зарядов, сопровождающегося так называемым электрическим ветром. может превысить значение, соответствующее ионизации воздуха (при нормальном атмосферном давлении Е’≈3*106 В/м), что приводит к возникновению стекания зарядов, сопровождающегося так называемым электрическим ветром.
Образующиеся при ионизации молекул электроны движутся к острию и компенсируют на нём часть заряда, равновесие зарядов на проводнике нарушается, и к острию подходят заряды с других участков поверхности проводника (см.рис.4.3). Такое движение продолжается до тех пор, пока модуль вектора 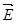 вблизи острия будет превышать вблизи острия будет превышать 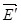 . Положительно заряженные ионы и заряды на поверхности проводника отталкиваются, что может привести к движению проводника. . Положительно заряженные ионы и заряды на поверхности проводника отталкиваются, что может привести к движению проводника.
4.2. Незаряженный проводник
во внешнем электрическом поле
Поместим во внешнее электрическое поле напряжённости 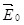 незаряженный проводник. незаряженный проводник.
Под действием сил поля свободные заряды в проводнике приходят в движение: положительные по полю, а отрицательные против поля.
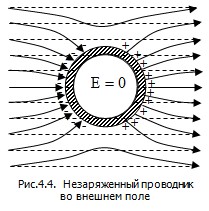 На одном конце проводника будет скапливаться избыток положительного, а на другом избыток отрицательного заряда. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника – перпендикулярными его поверхности (рис.4.4). Пунктиром показаны линии напряженности до внесения проводника в поле, а сплошные – линии напряженности после внесения. Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией. На одном конце проводника будет скапливаться избыток положительного, а на другом избыток отрицательного заряда. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника – перпендикулярными его поверхности (рис.4.4). Пунктиром показаны линии напряженности до внесения проводника в поле, а сплошные – линии напряженности после внесения. Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.
Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также равно нулю.
Итак, внешнее электрическое поле не проникает внутрь металла. Это позволяет, например, использовать металлическую оболочку, сплошную или в виде сетки, для защиты (экранировки) различных приборов от внешних электрических полей.
4.3. Электроёмкость проводника
Рассмотрим уединённый проводник, т.е. проводник который удалён от других тел. Его потенциал согласно (1.15) прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют различные потенциалы. Поэтому для уединённого проводника можно записать:
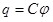 . .
Величину
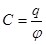 (4.3) (4.3)
называют электроёмкостью (или просто ёмкостью) уединённого проводника. Емкость уединённого проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника.
Единица электроёмкости – фарад (Ф); 1 Ф – емкость такого уединённого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1 Кл.
Потенциал уединённого шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью ε, равен:
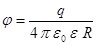 , ,
используя формулу (4.3), получаем емкость шара
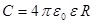
Отсюда следует, что емкостью 1 Ф обладал бы уединённый шар, находящийся в вакууме и имеющий радиус 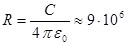 км, что примерно в 1400 раз больше радиуса Земли (электроёмкость Земли С≈0.7 мФ). Следовательно, фарад – очень большая величина, поэтому на практике используются дольные единицы – миллифарад (мФ), микрофарад (мкФ) и др. км, что примерно в 1400 раз больше радиуса Земли (электроёмкость Земли С≈0.7 мФ). Следовательно, фарад – очень большая величина, поэтому на практике используются дольные единицы – миллифарад (мФ), микрофарад (мкФ) и др.
4.4 Конденсаторы. Электроёмкость конденсаторов
Наибольший эффект увеличения электроёмкости проводника достигается для конденсаторов, представляющих собой две металлических пластины, разделённые слоем диэлектрика. На пластины (обкладки) подают заряды, одинаковые по модулю и противоположные по знаку. Форма конденсатора обеспечивает существование электрического поля только в пространстве между ними. Это позволяет устранить влияние на электроёмкость конденсатора окружающих его тел.
На рис.4.5 приведено схематическое изображение плоского, сферического и цилиндрического конденсаторов.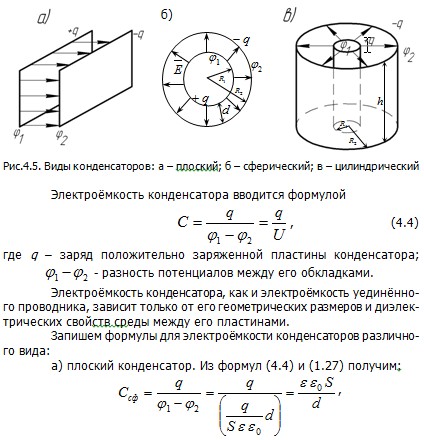
где S – площадь одной пластины конденсатора; d – расстояние между ними; ε – относительная диэлектрическая проницаемость среды между обкладками конденсатора;
б) сферический конденсатор. Радиусы обкладок обозначим R1 и R2 (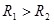 ). Электрическое поле конденсатора обладает сферической симметрией и согласно теореме Гаусса определяется зарядом только внутренней сферы. Учитывая формулу разности потенциалов между обкладками конденсатора (1.28), получаем: ). Электрическое поле конденсатора обладает сферической симметрией и согласно теореме Гаусса определяется зарядом только внутренней сферы. Учитывая формулу разности потенциалов между обкладками конденсатора (1.28), получаем:
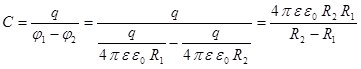 ; ;
в) электроёмкость цилиндрического конденсатора:
,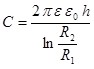
гдеh – высота конденсатора; R1и R2 – радиус внутренней и внешней поверхностей. |
|
|
